多层感知机
从这里开始真正的深度网络,最简单的深度网络称为多层感知机
多层感知机由多层神经元组成,每一层与它的上一层相连,从中接收输入;同时每一层也与它的下一层相连,影响当前层的神经元
多层感知机
隐藏层
在线性神经网络中讲到仿射变换,它是一种带有偏置项的线性变换
softmax回归通过单个仿射变换将输入直接映射到输出,然后进行softmax操作,标签通过仿射变换后确实与输入数据相关,但是仿射变换中的线性是一个很强的假设
线性模型的误差
线性意味着单调假设,任何特征的增大都会导致模型输出的增大,但这并不是在所有情况下都对
比如虽然收入与还款概率存在单调性,但它们不是线性相关的,处理这类问题的一种方法是使用对数进行预处理,使线性更合理
如何对猫和狗的图像进行分类呢?对线性模型的依赖对应于一个隐含的假设,即区分猫和狗的唯一要求是评估单个像素的强度,但是在一个倒置图像后依然保留类别的世界里,这种方法就会失败
在图像中,单个像素的意义几乎为零,像素的重要性取决于上下文——它周围像素的取值
如果能手动构造出一种新的特征表示,比如边缘特征、角点特征、梯度方向、颜色分布……,在这些“高级特征”上再用一个线性模型,就会表现很好,但我们并不知道怎么手工设计出这种完美的表示
对于深度神经网络,它不依赖人工设计特征,而是通过数据自动学习特征表示,也就是隐藏层
隐藏层的加入
可以通过在网络中加入一个或多个隐藏层来克服线性模型的限制,使其能处理更普遍的函数关系类型
最简单的方法是将许多全连接层堆叠在一起,每一层都输出到上面的层,直到生成最后的输出
可以把前$L-1$层看作表示,把最后一层看作线性预测器,这种架构通常称为多层感知机(multilayer perceptron),通常缩写为MLP

这个多层感知机有4个输入,3个输出,其隐藏层包含5个隐藏单元,输入层不涉及计算,所以这个多层感知机中的层数为2,同样是全连接层
因为全连接层的复杂度,即使在不改变输入或输出大小的情况下,可能在参数节约和模型有效性之间进行权衡
从线性到非线性
通过矩阵$\mathbf X \in \mathbb{R}^{n \times d}$来表示$n$个样本的小批量,其中每个样本具有$d$个输入特征
对于具有$h$个隐藏单元的单隐藏层多层感知机,用$\mathbf{H} \in \mathbb{R}^{n \times h}$表示隐藏层的输出,称为隐藏层变量(hidden-layer variable)
因为隐藏层和输出层都是全连接的,有隐藏层权重$\mathbf{W}^{(1)} \in \mathbb{R}^{d \times h}$和隐藏层偏置$\mathbf{b}^{(1)} \in \mathbb{R}^{1 \times h}$以及输出层权重$\mathbf{W}^{(2)} \in \mathbb{R}^{h \times q}$和输出层偏置$\mathbf{b}^{(2)} \in \mathbb{R}^{1 \times q}$,输出$\mathbf{O} \in \mathbb{R}^{n \times q}$
$$
\begin{split}\begin{aligned}
\mathbf{H} & = \mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}, \\
\mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}
\end{aligned}\end{split}
$$
在添加隐藏层之后,模型现在需要跟踪和更新额外的参数,但从这个模型上看并没有得到好处
因为对于任意权重值只需合并隐藏层,便可产生具有参数$\mathbf{W} = \mathbf{W}^{(1)}\mathbf{W}^{(2)}$和$\mathbf{b} = \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)}$的等价单层模型
$$
\mathbf{O} = (\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})\mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W}^{(1)}\mathbf{W}^{(2)} + \mathbf{b}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)} = \mathbf{X} \mathbf{W} + \mathbf{b}.
$$
为了发挥多层架构的潜力还需要一个额外的关键要素:在仿射变换之后对每个隐藏单元应用非线性的激活函数(activation function)
激活函数的输出$\sigma(\cdot)$被称为活性值(activations)
加入激活函数就不可能再将多层感知机退化成线性模型
$$
\begin{split}\begin{aligned}
\mathbf{H} & = \sigma(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)}), \\
\mathbf{O} & = \mathbf{H}\mathbf{W}^{(2)} + \mathbf{b}^{(2)}
\end{aligned}\end{split}
$$
出于记号习惯的考量,定义非线性函数也以按行的方式作用于其输入,即一次计算一个样本
大多数激活函数都是按元素计算,也就是说每个元素独立变换;但像 softmax这样的激活函数,还会按行归一化,也就是每个样本(行)内部的元素彼此关联
| 类型 | 示例 | 是否行内相关 | 输出含义 |
|---|---|---|---|
| 按元素 | ReLU, Sigmoid, Tanh | ❌ 否 | 非线性特征变换 |
| 按行 | Softmax | ✅ 是 | 概率归一化,类别竞争 |
为了构建更通用的多层感知机,可以继续堆叠这样的隐藏层,比如$\mathbf{H}^{(1)} = \sigma_1(\mathbf{X} \mathbf{W}^{(1)} + \mathbf{b}^{(1)})$,$\mathbf{H}^{(2)} = \sigma_2(\mathbf{H}^{(1)} \mathbf{W}^{(2)} + \mathbf{b}^{(2)})$,通过使用更深的网络,可以更容易地逼近许多函数
激活函数
**激活函数(activation function)**通过计算加权和并加上偏置来确定神经元是否应该被激活,大多数激活函数都是非线性的
ReLU函数
最受欢迎的激活函数是修正线性单元(Rectified linear unit,ReLU),因为它实现简单,同时在各种预测任务中表现良好
ReLU提供了一种非常简单的非线性变换,给定元素$x$,ReLU函数被定义为该元素与0的最大值
$$
\operatorname{ReLU}(x) = \max(x, 0).
$$
ReLU函数通过将相应的活性值设为0,仅保留正元素并丢弃所有负元素
1 | x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True) |
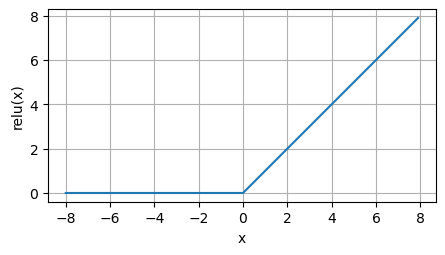
当输入为负时导数为0,而当输入为正时导数为1,当输入值等于0时ReLU函数不可导,默认使用左侧的导数,即输入0时导数为0
绘制其导数
1 | y.sum().backward(retain_graph=True) |
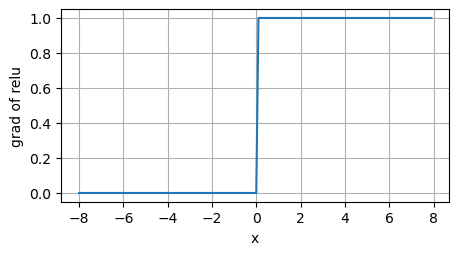
使用ReLU的原因是,它求导表现得特别好:要么让参数消失,要么让参数通过
这使得优化表现得更好,并且ReLU减轻了困扰以往神经网络的梯度消失问题
ReLU函数有许多变体,包括**参数化ReLU(Parameterized ReLU,pReLU)**函数
该变体为ReLU添加了一个线性项,因此即使参数是负的,某些信息仍然可以通过
$$
\operatorname{pReLU}(x) = \max(0, x) + \alpha \min(0, x).
$$
sigmoid函数
对于一个定义域在$\mathbb{R}$中的输入,sigmoid函数将输入变换为区间(0, 1)上的输出
因此,sigmoid通常称为挤压函数(squashing function)
$$
\operatorname{sigmoid}(x) = \frac{1}{1 + \exp(-x)}.
$$
当想要将输出视作二元分类问题的概率时,sigmoid仍然被广泛用作输出单元上的激活函数 (sigmoid可以视为softmax的特例)
但sigmoid在隐藏层中已经较少使用,它在大部分时候被更简单、更容易训练的ReLU所取代
1 | y = torch.sigmoid(x) |
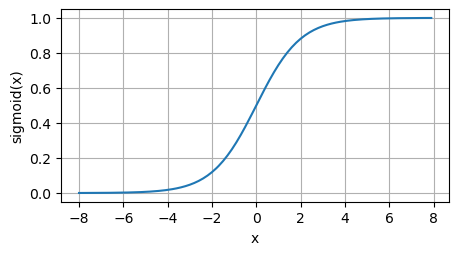
当输入接近0时,sigmoid函数接近线性变换
sigmoid函数的导数为
$$
\frac{d}{dx} \operatorname{sigmoid}(x) = \frac{\exp(-x)}{(1 + \exp(-x))^2} = \operatorname{sigmoid}(x)\left(1-\operatorname{sigmoid}(x)\right).
$$
当输入为0时,sigmoid函数的导数达到最大值0.25,而输入在任一方向上越远离0点时,导数越接近0
1 | x.grad.zero_() |
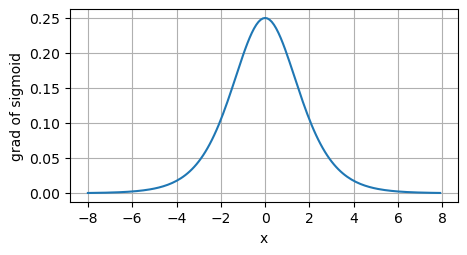
tanh函数
与sigmoid函数类似,tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上
$$
\operatorname{tanh}(x) = \frac{1 - \exp(-2x)}{1 + \exp(-2x)}
$$
当输入在0附近时,tanh函数接近线性变换
函数的形状类似于sigmoid函数,不同的是tanh函数关于坐标系原点中心对称
1 | y = torch.tanh(x) |
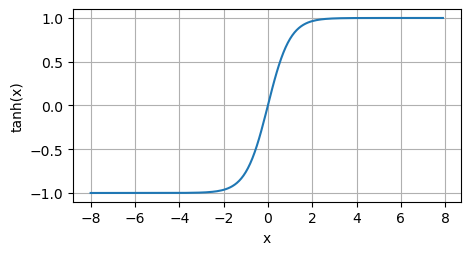
tanh函数的导数
$$
\frac{d}{dx} \operatorname{tanh}(x) = 1 - \operatorname{tanh}^2(x).
$$
tanh函数的导数和sigmoid类似,接近0时代最大值为1
1 | x.grad.zero_() |
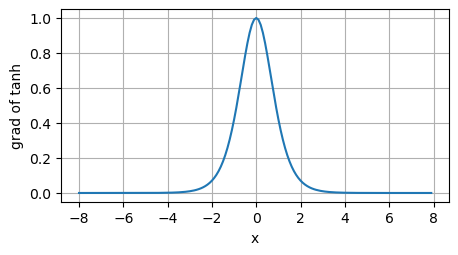
思考题
如果一个非线性激活函数不是按样本逐元素地应用,而是对整个小批量(batch)一起应用,会出现什么问题?
激活函数是对每个神经元输出进行非线性变换,应该逐样本、逐元素独立地工作
如果批量处理激活函数输出不再只取决于当前样本,而依赖于整个batch,这意味着模型对单个样本的预测结果会受到 batch 中其他样本的影响,就会导致样本之间互相干扰,打破独立性,造成梯度传播混乱,最终使模型难以收敛甚至失效
多层感知机的底层实现
为了与之前softmax回归获得的结果进行比较,将继续使用Fashion-MNIST图像分类数据集
1 | import torch |
初始化模型参数
将每个图像视为具有784个输入特征和10个类的简单分类数据集,将实现一个具有单隐藏层的多层感知机,它包含256个隐藏单元,可以将这两个变量都视为超参数
通常选择2的若干次幂作为层的宽度,因为内存在硬件中的分配和寻址方式,这么做往往可以在计算上更高效
对于每一层都要记录一个权重矩阵和一个偏置向量,要为损失关于这些参数的梯度分配内存
1 | num_inputs, num_outputs, num_hiddens = 784, 10, 256 |
激活函数
将实现ReLU激活函数,而不是直接调用内置的relu函数
1 | def relu(X): |
模型
因为忽略了空间结构,所以使用reshape将每个二维图像转换为一个长度为num_inputs的向量
1 | def net(X): |
损失函数
已经从零实现过softmax函数,在这里直接使用高级API中的内置函数来计算softmax和交叉熵损失
1 | loss = nn.CrossEntropyLoss(reduction='none') |
训练
多层感知机的训练过程与softmax回归的训练过程完全相同
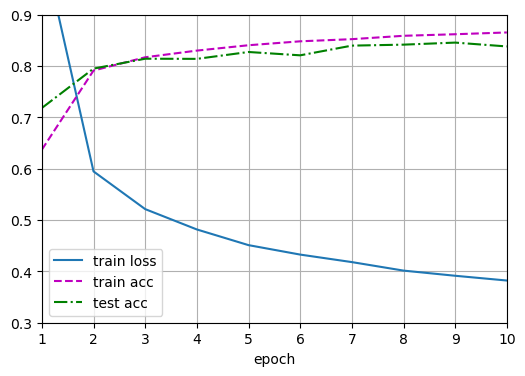
直接调用train_ch3函数,将迭代周期数设置为10,并将学习率设置为0.1
1 | num_epochs, lr = 10, 0.1 |
1 | Epoch 1/10: loss=1.0399, train_acc=0.634, test_acc=0.748 |
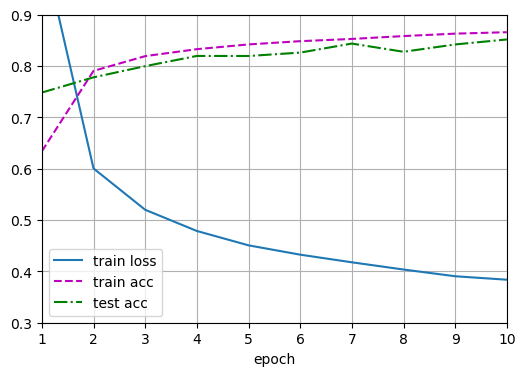
为了对学习到的模型进行评估,将在一些测试数据上应用这个模型
1 | predict_ch3(net, test_iter) |

测试结果是一样的
思考题
改变 num_hiddens 会影响什么?
- 太小:模型容量不足(underfitting) → 学不出复杂特征
- 适中:模型能恰好捕捉数据规律
- 太大:模型容量过大(overfitting) → 训练集精度高但测试集差
隐藏层层数增加对结果有什么影响?
增加特征层级抽象能力,但可能会出现过拟合的情况
多层感知机的简洁实现
模型
与softmax回归实现相比,唯一的区别是添加了2个全连接层
第一层是隐藏层,它包含256个隐藏单元,并使用了ReLU激活函数,第二层是输出层
1 | net = nn.Sequential( |
这种模块化设计能够将与模型架构有关的内容独立出来
训练
1 | batch_size, lr, num_epochs = 256, 0.1, 10 |
1 | Epoch 1/10: loss=1.0426, train_acc=0.637, test_acc=0.718 |
模型选择、欠拟合和过拟合
机器学习科学家的目标是发现模式(pattern),这些模式捕捉到了训练集潜在总体的规律
如何发现可以泛化的模式是机器学习的根本问题
将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合(overfitting),用于对抗过拟合的技术称为正则化(regularization)
训练误差和泛化误差
训练误差(training error):模型在训练数据上的平均错误
泛化误差(generalization error):模型在“从未见过”的新样本上的平均错误
泛化误差无法精确计算,因为真实数据分布是无限的,只能用独立的测试集(由未参与训练的随机样本组成)来近似估计它
统计学习理论
假设训练数据和测试数据都是从相同的分布中独立提取的(独立同分布假设),这意味着对数据进行采样的过程没有进行“记忆”
即使这一假设被轻微违反,模型通常仍能良好工作,因为现实数据几乎总会偏离独立同分布
模型复杂性
当模型简单、数据充足时,训练误差与泛化误差接近
当模型复杂、样本较少时,训练误差下降但泛化误差上升
影响模型泛化的因素
- 模型复杂度,参数(自由度)越多越易过拟合
- 权重大小,权重的取值范围越大越易过拟合
- 训练样本的数量,样本越多越不易过拟合
模型选择
在机器学习中通常在评估几个候选模型后选择最终的模型,这个过程叫做模型选择
比较内容可以是不同模型类型(如决策树与线性模型),也可以是同模型的不同超参数(如层数、单元数、激活函数等)
为了确定候选模型中的最佳模型,通常会使用验证集
验证集
在进行训练前一般将数据分成三份,训练集、测试集、验证集(validation set)
验证集用于调整模型结构和超参数,但在实践中验证集与测试集往往来自同一数据源
因此输出的准确度其实是验证集准确度,而不是测试集准确度
K折交叉验证
当训练数据稀缺时,往往难以划分出足够的验证集
一种常用的解决方案是K 折交叉验证:
将原始训练数据划分为 K 个互不重叠的子集,每次使用其中 K−1 个子集进行训练,剩下的一个用于验证
重复 K 次后,对所有验证结果取平均,以更可靠地估计模型的训练与验证误差
欠拟合/过拟合
当训练误差和验证误差都很高时,说明模型无法有效拟合训练数据,通常表示模型过于简单、表达能力不足,被称为欠拟合(underfitting)
当训练误差远低于验证误差时,则说明模型在训练集上表现良好,却无法泛化到新数据,被称为过拟合(overfitting)
模型是否欠拟合或过拟合,取决于其复杂度与可用训练数据量的平衡
设训练数据由单个特征$x$和对应实数标签$y$组成,尝试用$d$阶多项式拟合
$$
\hat y= \sum_{i=0}^d x^i w_i
$$
这是一个线性回归问题,只不过输入特征为$x$的幂次
其中$w_i$为模型权重,$w_0$为偏置,损失函数采用平方误差
显然,高阶多项式的参数更多,模型更复杂,能表示的函数形状更灵活
在相同训练数据下,高阶多项式模型的训练误差通常会小于等于低阶多项式模型的训练误差
多项式回归
生成数据集
使用以下三阶多项式来生成训练和测试数据的标签:
$$
y = 5 + 1.2x - 3.4\frac{x^2}{2!} + 5.6 \frac{x^3}{3!} + \epsilon \text{ where }
\epsilon \sim \mathcal{N}(0, 0.1^2).
$$
在优化的过程中,通常希望避免非常大的梯度值或损失值,所以将特征从$x^i$调整为$x^i/i!$,这样可以避免很大的$i$带来的特别大的指数值
将为训练集和测试集各生成100个样本
1 | import random |
存储在poly_features中的单项式由gamma函数重新缩放
训练和测试
实现一个函数来评估模型在给定数据集上的损失
1 | def evaluate_loss(net, data_iter, loss): #@save |
定义训练函数
1 | def train(train_features, test_features, train_labels, test_labels, |
三阶多项式函数拟合(正常)
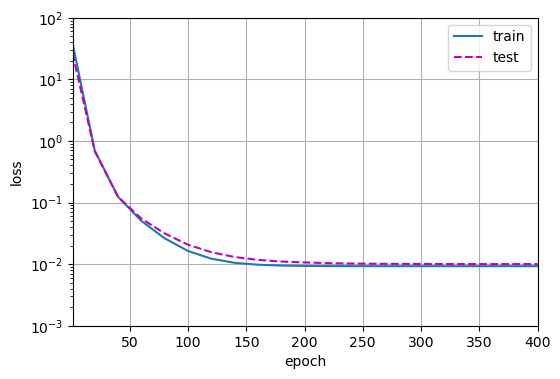
首先使用三阶多项式函数,它与数据生成函数的阶数相同,结果表明,该模型能有效降低训练损失和测试损失
1 | # 从多项式特征中选择前4个维度,即1,x,x^2/2!,x^3/3! |
1 | weight: [[ 5.0210333 1.2359931 -3.4435396 5.543001 ]] |
学习到的模型参数也接近真实值$w = [5, 1.2, -3.4, 5.6]$
线性函数拟合(欠拟合)
线性函数拟合,减少该模型的训练损失相对困难
当用来拟合非线性模式(如这里的三阶多项式函数)时,线性模型容易欠拟合
1 | # 从多项式特征中选择前2个维度,即1和x |
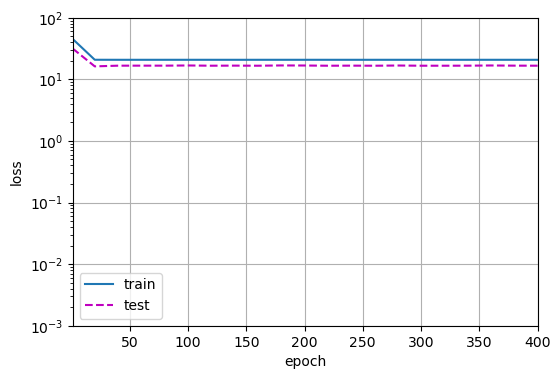
1 | weight: [[3.1353095 5.6418805]] |
高阶多项式函数拟合(过拟合)
在这种情况下,没有足够的数据用于学到高阶系数应该具有接近于零的值
虽然训练损失可以有效地降低,但测试损失仍然很高,结果表明,复杂模型对数据造成了过拟合
1 | # 从多项式特征中选取所有维度 |
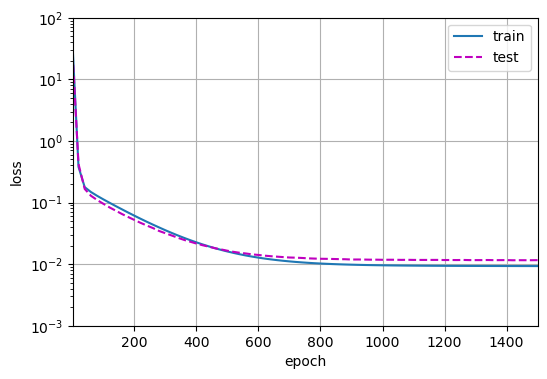
1 | weight: [[ 5.0239668e+00 1.3013747e+00 -3.4798586e+00 5.2033052e+00 |
可以看到训练损失和测试损失的差值比三阶的更大了,因为一开始做了阶乘归一化,而且这里的训练次数也改到了1500所以不会导致很明显的过拟合
权重衰减
虽然增加训练数据量可以有效降低过拟合风险,但这往往代价高昂、耗时漫长,短期内难以实现
在数据量已接近可行上限的情况下,通常将重点转向正则化方法
在前面的多项式拟合中通过调整多项式的阶数来限制模型的容量,限制特征的数量是缓解过拟合的一种常用技术
在多变量情形中,多项式扩展为由多个变量的幂次乘积构成的单项式(monomials),单项式的阶数是各变量幂次之和,例如$x_1^2 x_2$和$x_3 x_5^2$都是3次单项式
随着阶数$d$的增长,单项式的数量迅速膨胀
给定$k$个变量,阶数为$d$的项的个数为
$$
\binom{k-1+d}{k-1}=\frac{(k-1+d)!}{d!(k-1)!}
$$
这意味着阶数的微小提升都会显著提高模型的复杂度
因此仅仅依靠限制特征数量仍可能使模型在过于简单与过于复杂之间摇摆,需要一个更精细可控的手段来调节函数的复杂性,使模型在两者之间取得平衡
范数与权重衰减
在训练参数化机器学习模型时,**权重衰减(weight decay)**是最常用的正则化方法之一,也被称为$L_2$正则化,通过约束参数向量与零的距离来控制模型复杂度,从而防止过拟合
对于线性模型$f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x}$ 希望权重向量不要过大,常见做法是在损失函数中加入权重的平方范数惩罚项,调整为最小化预测损失和惩罚项之和
通过正则化常数$\lambda$来描述这种权衡,这是一个非负超参数
$$
L(\mathbf{w}, b) + \frac{\lambda}{2}\mid\mid \mathbf{w} \mid\mid^2
$$
对于$\lambda = 0$恢复了原来的损失函数,对于$\lambda > 0$限制$\mid\mid \mathbf{w} \mid\mid^2$的大小
为什么在这里使用平方范数而不是标准范数(即欧几里得距离)?
平方$L_2$范数保留了权重平方和的形式,使得惩罚的导数很容易计算,导数的和等于和的导数
$$
\frac{\partial}{\partial w_{i}} \frac{1}{2}\mid\mid \mathbf{w} \mid\mid^2=\frac{\partial}{\partial w_{i}} \frac{1}{2} \sum_{j} w_{j}^{2}=w_{i}
$$
为什么使用$L_2$范数,而不是$L_1$范数
$L_2$正则化对应岭回归(ridge regression)算法,会对权重的较大分量施加更强惩罚,使权重在多个特征上平滑分布,从而提高模型对噪声和观测误差的稳定性
$L_1$正则化线对应套索回归(lasso regression)会将部分权重推到零,实现特征选择(feature selection)
两者都能抑制过拟合,但$L_2$更适合连续平滑的参数调整,$L_1$更适合产生稀疏解
$L_2$正则化回归的小批量随机梯度下降更新如下式
$$
\begin{aligned}
\mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right).
\end{aligned}
$$
权重衰减+普通梯度下降,通常网络输出层的偏置项不会被正则化
高维线性回归
通过一个简单的例子来演示权重衰减,生成一些数据:
$$
y = 0.05 + \sum_{i = 1}^d 0.01 x_i + \epsilon \text{ where }
\epsilon \sim \mathcal{N}(0, 0.01^2).
$$
选择标签是关于输入的线性函数,标签同时被均值为0,标准差为0.01高斯噪声破坏
为了使过拟合的效果更加明显,可以将问题的维数增加到$d = 200$,并使用一个只包含20个样本的小训练集
1 | def synthetic_data(w, b, num_examples): #@save |
底层实现
初始化模型参数
1 | def init_params(): |
定义L2范数惩罚
最方便的方法是对所有项求平方后并将它们求和
1 | def l2_penalty(w): |
定义训练代码
唯一的变化是损失加上惩罚项
1 | def train(lambd): |
无正则化
用lambd = 0禁用权重衰减后运行这个代码,这里训练误差有了减少,但测试误差没有减少,这意味着出现了严重的过拟合
1 | train(lambd=0) |
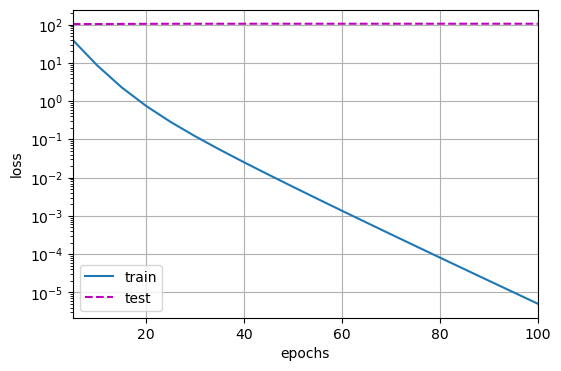
1 | w的L2范数是: 14.787172317504883 |
权重衰减
使用权重衰减来运行代码,在这里训练误差增大,但测试误差减小,这正是期望从正则化中得到的效果
1 | train(lambd=3) |
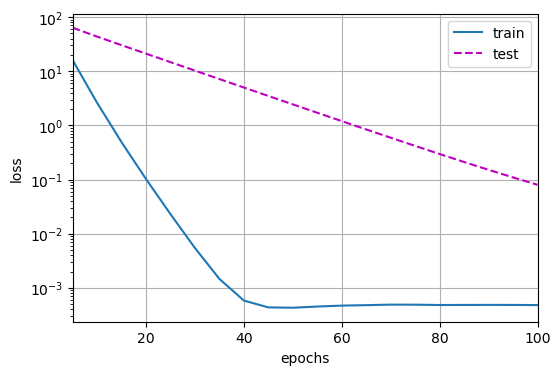
1 | w的L2范数是: 0.354495644569397 |
能看出如果不加权重衰减很容易陷入过拟合
简洁实现
深度学习框架将权重衰减直接集成到优化算法中,使其能够与任意损失函数方便结合
在实例化优化器时只需通过 weight_decay 参数即可指定权重衰减系数
在 PyTorch 中,默认情况下优化器会同时对权重参数和偏置参数施加衰减,这里只为权重设置了weight_decay,所以偏置参数不会衰减
1 | def train_concise(wd): |
1 | train_concise(0) |
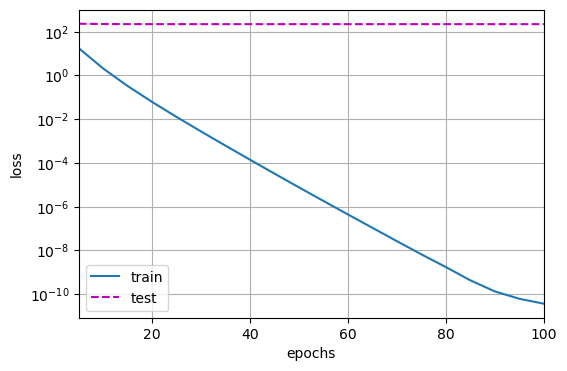
1 | w 的范数: 13.793038368225098 |
结果和从零开始实现权重衰减时的图相同,然而它们运行得更快,更容易实现
1 | train_concise(3) |
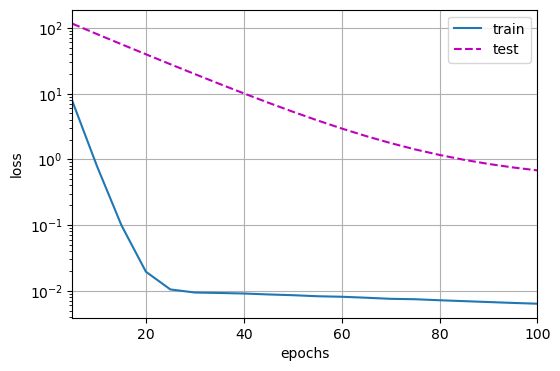
1 | w 的范数: 0.3899060785770416 |
小结
- 正则化是处理过拟合的常用方法:在训练集的损失函数中加入惩罚项,以降低学习到的模型的复杂度
- 保持模型简单的一个特别的选择是使用$L_2$惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减
- 在同一训练代码实现中,不同的参数集可以有不同的更新行为
思考题
训练与测试精度随 λ 变化的趋势
测试误差先下降后上升,呈 U 形曲线
正则化太弱 → 过拟合;正则化太强 → 欠拟合
使用验证集来找到$\lambda$最佳值。它真的是最优值吗?这有关系吗?
是相对于这个训练集和验证集的最优值,会根据数据集大小发生变化
如果使用$L_1$正则化作为选择的惩罚,那么代码如何修改
1
2
3
4
5
6
7def l1_penalty(w):
return torch.sum(torch.abs(w))
...
trainer = torch.optim.SGD(net.parameters(), lr=lr)
...
l = l.mean() + lambd * l1_penalty(net[0].weight)
...
暂退法Dropout
扰动的稳健性
一个“好”的预测模型,不仅要在训练数据上表现良好,更重要的是能在未知数据上保持较高的准确度。经典的泛化理论认为,为了缩小训练和测试性能之间的差距,应追求模型的简单性
简单性可以通过多种形式体现:较低的模型维度、更小的参数范数,或是更平滑的函数行为
平滑性意味着模型对输入的微小变化不敏感——在图像分类中,轻微的像素噪声不应影响预测结果
1995年,克里斯托弗·毕晓普(Christopher Bishop)证明了在训练过程中向输入添加高斯噪声,与Tikhonov正则化(即$L_2$正则化)在数学上是等价的,这说明函数对输入噪声具有鲁棒性,本质上也是在约束其平滑性
2014年,斯里瓦斯塔瓦等人将这一思想推广到神经网络的内部层,提出在训练时向每一层的输出中注入随机噪声,以增强输入–输出映射的平滑性,这便是暂退法(dropout),通过在前向传播时随机丢弃部分神经元的激活值来实现正则化,这已经成为训练神经网络的常用技术
为了避免引入偏差,dropout采用无偏噪声注入方式,每个中间激活值$h$以暂退概率$p$被置零,保留下来的放大为$h/(1-p)$,$h’$表示为
$$
\begin{split}\begin{aligned}
h’ =
\begin{cases}
0 & \text{ 概率为 } p \\
\frac{h}{1-p} & \text{ 其他情况}
\end{cases}
\end{aligned}\end{split}
$$
这样保证其期望值不变$E[h’] = h$
原理图
之前的多层感知机中带有1个隐藏层和5个隐藏单元,将暂退法应用到隐藏层,以$p$的概率将隐藏单元置为零,相当于每次训练时使用原网络的一个子网络
使得输出层的计算不能过度依赖于$h_1, \ldots, h_5$的任何一个元素,提高模型的泛化性
测试阶段不使用dropout,也无需缩放;若模型在多次随机遮盖后仍能给出一致预测,说明其具有良好的稳定性与鲁棒性
底层实现
要实现单层的暂退法函数,可以从均匀分布$U[0, 1]$中生成与该层神经元维度相同的随机张量,保留其中大于丢弃概率$p$的元素,其余置零
dropout_layer 函数:以dropout的概率丢弃张量输入X中的元素,再将剩余部分除以1.0-dropout
1 | def dropout_layer(X, dropout): |
将输入X通过暂退法操作,暂退概率分别为0、0.5和1来测试dropout_layer函数
1 | X = torch.arange(16).reshape((2,8)) |
定义模型参数
同样使用Fashion-MNIST数据集,定义具有两个隐藏层的多层感知机,每个隐藏层包含256个单元
1 | num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256 |
定义模型
在网络中,通常在每个隐藏层的激活函数之后应用暂退法,并为不同层设置各自的暂退概率
通常在靠近输入层的位置使用较小的暂退概率,而在更深层使用较大的暂退概率,以在保留关键信息的同时增强模型的正则化效果
下面的模型将第一个和第二个隐藏层的暂退概率分别设置为0.2和0.5,并且暂退法只在训练期间有效
1 | class Net(nn.Module): |
1 | 输入层 → 全连接层1 → ReLU → Dropout1 → 全连接层2 → ReLU → Dropout2 → 输出层 |
训练和测试
类似于前面描述的多层感知机训练和测试
1 | num_epochs, lr, batch_size = 10, 0.5, 256 |
1 | Epoch 1/10: loss=0.8763, train_acc=0.672, test_acc=0.768 |
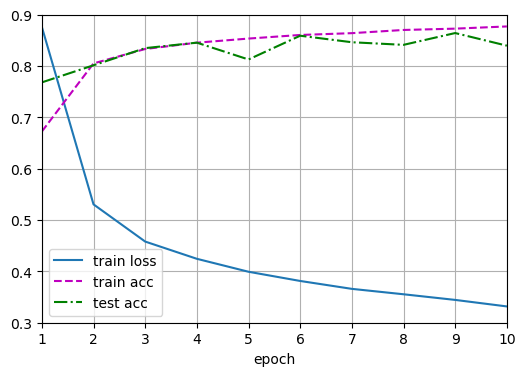
简洁实现
对于深度学习框架,只需在每个全连接层之后添加一个Dropout层,将暂退概率作为唯一的参数传递给它的构造函数
在训练时,Dropout层将根据指定的暂退概率随机丢弃上一层的输出(相当于下一层的输入)
在测试时,Dropout层仅传递数据
1 | dropout1, dropout2 = 0.2, 0.5 |
对模型进行训练和测试
1 | dropout1, dropout2 = 0.2, 0.5 |
1 | Epoch 1/10: loss=1.1567, train_acc=0.555, test_acc=0.721 |
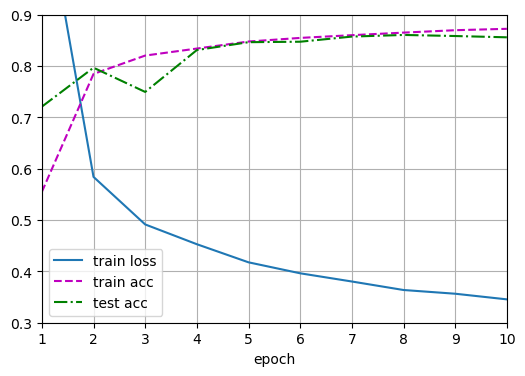
小结
- 暂退法在前向传播过程中,计算每一内部层的同时丢弃一些神经元
- 暂退法可以避免过拟合,它通常与控制权重向量的维数和大小结合使用的
- 暂退法将活性值替换为具有相同期望值的随机变量
- 暂退法仅在训练期间使用
对比一下Dropout与权重衰减
| 正则化方式 | 控制复杂度的方式 | 直观效果 | 正则对象 |
|---|---|---|---|
| 权重衰减 | 直接惩罚权重的$L_2$范数 抑制参数变大 |
让模型“更平滑” 权重分布更均匀 |
参数空间的正则化 |
| 暂退法 | 训练时随机屏蔽部分神经元输出 防止神经元共适应 |
让模型“更稀疏” 逼迫网络学习多种子结构 |
结构空间的正则化 |
二者都能降低模型方差、增强泛化,但机制互补
同时使用暂退法和权重衰减不会互相抵消,但会出现正则化叠加的边际效应递减,反而可能导致欠拟合或性能下降
一般根据任务类型选择其一:
- Dropout → 对高维输入(如图像、文本)特别有效
- $L_2$ → 对权重尺度敏感的任务(如回归或线性模型)常用
思考题
如果将暂退法应用到权重矩阵的各个权重,而不是激活值,会发生什么?
如果把 Dropout 施加到权重矩阵上,模型会变成类似DropConnect(Wan et al., 2013)的形式,随机屏蔽神经元连接,而非神经元输出,它理论上更强,但训练更噪、更慢、不稳定
计算图
已经学习了如何用小批量随机梯度下降训练模型,但实现过程中只考虑了通过前向传播(forward propagation)所涉及的计算,在计算梯度时,只调用了深度学习框架提供的反向传播函数,而不知其所以然
梯度的自动计算(自动微分)大大简化了深度学习算法的实现,现在来探讨反向传播的细节
前向传播
前向传播(forward propagation或forward pass)指的是按顺序(从输入层到输出层)计算和存储神经网络中每层的结果
假设输入样本是$\mathbf{x}\in \mathbb{R}^d$,并且隐藏层不包括偏置项,这里的中间变量是
$$
\mathbf{z}= \mathbf{W}^{(1)} \mathbf{x}
$$
其中$\mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}$是隐藏层的权重参数,将中间变量$\mathbf{z}\in \mathbb{R}^h$通过激活函数后,得到长度为$h$的隐藏激活向量
$$
\mathbf{h}= \phi (\mathbf{z})
$$
假设输出层的参数只有权重$\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$,可以得到输出层变量,它是一个长度为$q$的向量
$$
\mathbf{o}= \mathbf{W}^{(2)} \mathbf{h}
$$
假设损失函数为$l$,样本标签为$y$,单个数据样本的损失项
$$
L = l(\mathbf{o}, y)
$$
根据$L_2$正则化的定义,给定超参数$\lambda$,正则化项为
$$
s = \frac{\lambda}{2} \left(\mid\mid\mathbf{W}^{(1)}\mid\mid_F^2 + \mid\mid\mathbf{W}^{(2)}\mid\mid_F^2\right),
$$
模型在给定数据样本上的正则化损失为
$$
J = L + s
$$
将$J$称为目标函数
前向传播计算图
绘制计算图有助于可视化计算中操作符和变量的依赖关系
与上述简单网络相对应的计算图
其中正方形表示变量,圆圈表示操作符
左下角表示输入,右上角表示输出
反向传播
**反向传播(backward propagation或backpropagation)**指的是计算神经网络参数梯度的方法
该方法根据微积分中的链式规则,按相反的顺序从输出层到输入层遍历网络
算法存储了计算某些参数梯度时所需的任何中间变量(偏导数)
根据链式法则得到
$$
\begin{aligned}\frac{\partial J}{\partial \mathbf{W}^{(1)}}
= \text{prod}\left(\frac{\partial J}{\partial \mathbf{z}}, \frac{\partial \mathbf{z}}{\partial \mathbf{W}^{(1)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(1)}}\right)
= \frac{\partial J}{\partial \mathbf{z}} \mathbf{x}^\top + \lambda \mathbf{W}^{(1)}\\
\frac{\partial J}{\partial \mathbf{W}^{(2)}}= \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{W}^{(2)}}\right) + \text{prod}\left(\frac{\partial J}{\partial s}, \frac{\partial s}{\partial \mathbf{W}^{(2)}}\right)= \frac{\partial J}{\partial \mathbf{o}} \mathbf{h}^\top + \lambda \mathbf{W}^{(2)} \end{aligned}
$$
训练神经网络
在训练神经网络时,前向传播和反向传播相互依赖
以上述简单网络为例
前向传播期间计算正则项取决于模型参数$\mathbf{W}^{(1)}$和$\mathbf{W}^{(2)}$的当前值,是由优化算法根据最近迭代的反向传播给出的
反向传播期间参数的梯度计算,取决于由前向传播给出的隐藏变量$\mathbf{h}$的当前值
稳定性和初始化
初始化方案的选择在神经网络学习中起着举足轻重的作用,它对保持数值稳定性至关重要
选择哪个函数以及如何初始化参数可以决定优化算法收敛的速度有多快
稳定性
考虑一个具有$L$层、输入$\mathbf{x}$和输出$\mathbf{o}$的深层网络,如果所有隐藏变量和输入都是向量,可以将$\mathbf{o}$关于任何一组参数$\mathbf{W}^{(l)}$的梯度写为下式
$$
\partial_{\mathbf W^{(l)}} \mathbf o = \underbrace{\partial_{\mathbf h^{(L-1)}} \mathbf h^{(L)}}{ \mathbf M^{(L)} \stackrel{\mathrm{def}}{=}} \cdot \ldots \cdot \underbrace{\partial{\mathbf h^{(l)}} \mathbf h^{(l+1)}}{ \mathbf M^{(l+1)} \stackrel{\mathrm{def}}{=}} \underbrace{\partial{\mathbf W^{(l)}} \mathbf h^{(l)}}_{ \mathbf v^{(l)} \stackrel{\mathrm{def}}{=}}.
$$
该梯度是$L-l$个矩阵$\mathbf{M}^{(L)} \cdot \ldots \cdot \mathbf{M}^{(l+1)}$与梯度向量$\mathbf{v}^{(l)}$的乘积,容易受到数值上下溢问题的影响
不稳定梯度也威胁到优化算法的稳定性
- 梯度爆炸(gradient exploding)问题:参数更新过大,破坏了模型的稳定收敛
- 梯度消失(gradient vanishing)问题:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习
神经网络在参数化中存在对称性问题,隐藏层的多个单元可以通过权重重排获得相同的函数
若所有隐藏单元用相同参数初始化,它们在前向传播中输出相同激活,反向传播中获得相同梯度,训练过程无法打破这种对称性,网络退化为仅一个有效单元,表达能力大幅下降
虽然梯度下降无法打破这种对称性,但暂退法可通过随机扰动有效缓解这一问题
参数初始化
解决上述问题的一种方法是进行参数初始化,适当的正则化也可以进一步提高稳定性
默认初始化
如果不指定初始化方法,框架将使用默认的随机初始化方法,对于中等难度的问题,这种方法通常很有效
根据不同层的类型,默认初始化方式也不相同
| 层类型 | 默认初始化 | 说明 |
|---|---|---|
nn.Linear nn.Conv2d |
Kaiming Uniform | 适合 ReLU 系激活 |
nn.BatchNorm |
权重=1,偏置=0 | 保持尺度一致 |
nn.Embedding |
均匀分布 U(-1, 1) | 向量随机初始化 |
nn.LSTM nn.GRU |
Xavier Uniform(Glorot) | 平衡输入与输出方差 |
Xavier初始化
Xavier(Glorot)初始化是深度学习中最早、最经典的权重初始化方法之一
核心思想:让每层的输入和输出方差尽量相同,从而保持信号在网络中传播时的尺度稳定
为了让前向传播和反向传播都稳定
$$
Var(w)=\frac{2}{n_{in}+n_{out}}
$$
$n_{in}$:该层输入单元数
$n_{out}$:该层输出单元数
使得输入信号在传播到下一层时既不会放大也不会衰减
提供了两种分布形式:均匀分布(Pytorch默认)和正态分布
$$
w \sim U\left(-\sqrt{\frac{6}{n_{in}+n_{out}}}, \sqrt{\frac{6}{n_{in}+n_{out}}}\right)
$$
尽管在其数学推理中“不存在非线性”的假设在神经网络中很容易被违反,但Xavier初始化方法在实践中被证明是有效的
Kaiming初始化
Kaiming(He)初始化是一种专门为 ReLU 及其变体设计的权重初始化方法
核心思想:让每层的输出方差与输入方差保持一致,使信号在深层网络中既不过强也不过弱
如果输入是独立的零均值变量,而 ReLU 会把一半的输入变为 0,为了维持方差恒定需要满足
$$
Var(w)=\frac{2}{n_{in}}
$$
提供了两种分布形式:均匀分布(Pytorch默认)和正态分布
$$
w \sim U\left(-\sqrt{\frac{6}{n_{i n}}}, \sqrt{\frac{6}{n_{i n}}}\right)
$$
对称性问题
神经网络中的“对称性”往往意味着“参数冗余”
若多个单元、通道、时间步或模块在初始时完全相同,它们在训练中将始终保持相同,无法学习到互补特征
通过随机初始化、正则化或结构差异来打破对称性,是让网络具备表达力与泛化能力的关键
| 网络类型 | 对称性来源 | 后果 | 打破方法 |
|---|---|---|---|
| MLP | 隐藏单元可交换 | 单元退化为相同功能 | 随机初始化、dropout |
| CNN | 通道交换 | 特征图重复 | 随机初始化、BN |
| RNN/LSTM | 时间步相同 | 无时间差异 | 随机初始化、输入扰动 |
| Transformer | 注意力头可交换 | 多头退化为单头 | 独立头部初始化 |
| Autoencoder | 编解码镜像 | 恒等映射 | 独立参数、噪声 |
| GAN | G/D 对称博弈 | 模式坍塌 | 不同学习率、G/D异步更新 |
分布偏移
在理想条件下,通常假设训练集和测试集都是从同一分布独立采样得到的(独立同分布)
但现实中,这个假设几乎总是被打破,于是模型在训练环境中表现很好,却在新环境下表现糟糕,这就是分布偏移(distribution shift)
当这种分布差异是由外部环境变化(如天气、地域、设备差异等)导致的,也称之为环境偏移(environment shift)
分布偏移类型
协变量偏移
在不同分布偏移中,**协变量偏移(covariate shift)**可能是最为广泛研究的
假设:
- 输入数据的分布$P(\mathbf{x})$改变了
- 但输入与标签之间的映射关系$$P(y\mid \mathbf{x})$$保持不变
比如猫狗分类问题,训练使用真实拍摄图片,测试使用卡通图片
标签偏移
**标签偏移(label shift)**描述了与协变量偏移相反的问题
假设:
- 各类样本的比例$P(y)$发生变化
- 同一类别的样本外观(或特征分布)$$P(\mathbf{x} \mid y)$$不变
当认为$y$导致$\mathbf{x}$时,标签偏移是一个合理的假设,例如预测患者的疾病,可能根据症状来判断
概念偏移
概念偏移/条件偏移:$P(\mathbf{x})$和$P(y)$可能没发生改变,但$P(y\mid \mathbf x)$发生改变了
输入与标签的关系变了
比如不同地区对一个词的解释是不一样的,不同国家的交通指示不一样
学习问题的分类法
批量学习
在**批量学习(batch learning)**中,可以访问一组训练特征和标签${(\mathbf{x}_1, y_1), \ldots, (\mathbf{x}_n, y_n)}$,使用这些特性和标签训练$f(\mathbf{x})$,然后部署此模型来对来自同一分布的新数据进行评分,基本再也不会更新
在线学习
除了“批量”地学习,还可以单个“在线”学习数据$(\mathbf{x}_i, y_i)$
首先观测到$\mathbf{x}_i$,得出一个估计值$f(\mathbf{x}_i)$,当做到这一点后才观测到$y_i$,根据决定会得到奖励或损失
许多实际问题都属于这一类
在**在线学习(online learning)**中有以下的循环,在这个循环中给定新的观测结果会不断地改进模型
$$
\mathrm{model} ~ f_t \rightarrow
\mathrm{data} ~ \mathbf x_t \rightarrow
\mathrm{estimate} ~ f_t(\mathbf x_t) \rightarrow
\mathrm{observation} ~ y_t \rightarrow
\mathrm{loss} ~ l(y_t, f_t(\mathbf x_t)) \rightarrow
\mathrm{model} ~ f_{t+1}
$$
老虎机
**老虎机(bandits)**是上述问题的一个特例,虽然在大多数学习问题中有一个连续参数化的函数$f$,
但在一个老虎机问题中,可以采取的行动是有限的,面对多个未知收益的选择,每次只能选择一个行动并获得反馈
探索与利用之间的权衡,常见贪心算法
强化学习
**强化学习(reinforcement learning)**强调如何基于环境而行动,以取得最大化的预期利益
国际象棋、围棋、西洋双陆棋或星际争霸都是强化学习的应用实例
类似老虎机,但是强化学习的奖励是延迟的
与监督学习的区别
| 维度 | 监督学习 | 强化学习 |
|---|---|---|
| 训练数据 | 已知输入–输出对 | 通过环境交互生成 |
| 目标 | 最小化预测误差 | 最大化长期回报 |
| 反馈 | 即时且确定 | 延迟且随机 |
| 学习方式 | 离线学习 | 在线学习(边探索边更新) |
| 典型问题 | 分类 / 回归 | 决策 / 控制 |
Kaggle实践
Kaggle的房价预测比赛,此数据集由Bart de Cock于2011年收集,涵盖了2006-2010年期间亚利桑那州埃姆斯市的房价,它比哈里森和鲁宾菲尔德的波士顿房价数据集要大得多,也有更多的特征
下载和缓存数据集
首先建立字典DATA_HUB,它可以将数据集名称的字符串映射到数据集相关的二元组上,这个二元组包含数据集的url和验证文件完整性的sha-1密钥,所有类似的数据集都托管在地址为DATA_URL的站点上
1 | import hashlib |
download函数用来下载数据集,如果缓存目录中已经存在此数据集文件,并且其sha-1与存储在DATA_HUB中的相匹配,将使用缓存的文件,以避免重复的下载
1 | def download(name, cache_dir="data"): #@save |
还需实现两个实用函数:一个将下载并解压缩一个zip或tar文件,另一个是将使用的所有数据集从DATA_HUB下载到缓存目录中
1 | def download_extract(name, folder=None): #@save |
Kaggle
Kaggle是一个当今流行举办机器学习比赛的平台,每场比赛都以至少一个数据集为中心
在房价预测比赛页面的“Data”选项卡下可以找到数据集
访问和读取数据集
为方便起见可以使用上面定义的脚本下载并缓存Kaggle房屋数据集
1 | DATA_HUB['kaggle_house_train'] = ( #@save |
将使用pandas读入并处理数据
1 | train_data = pd.read_csv(download('kaggle_house_train')) |
1 | print(train_data.shape) # (1460, 81) |
训练数据集包括1460个样本,每个样本80个特征和1个标签,测试数据集包含1459个样本,每个样本80个特征
查看前四个和最后两个特征,以及相应标签(房价)
1 | print(train_data.iloc[0:4,[0,1,2,3,-3,-2,-1]]) |
1 | Id MSSubClass MSZoning LotFrontage SaleType SaleCondition SalePrice |
可以看到,在每个样本中,第一个特征是ID,这有助于模型识别每个训练样本,但是并不携带任何信息,所以要删除该列
1 | all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:])) |
训练集去掉Id和SalePrice,测试集只去掉Id列
数据预处理
在开始建模之前需要对数据进行预处理,需要将缺失值替换为相应特征的平均值
为了将所有特征放在一个共同的尺度上,通过将特征重新缩放到零均值和单位方差来标准化数据
$$
x \leftarrow \frac{x - \mu}{\sigma}
$$
| 模型类型 | 是否依赖标准化 | 原因 |
|---|---|---|
| 线性回归 / 逻辑回归 | 必须 | 梯度更新受特征尺度影响 |
| 神经网络 | 强烈建议 | 有助于稳定训练、加快收敛 |
| SVM / KNN / PCA | 必须 | 这些算法都依赖特征间的距离 |
| 决策树 / 随机森林 | 不需要 | 树模型只关心特征的相对大小或阈值分割,不受尺度影响 |
标准化数据的原因:
- 消除不同特征的量纲影响
- 让梯度下降更快、更稳定
- 避免某些特征主导模型学习
number类型数据处理:
1 | # 选出所有数值类型的特征列 |
离散数据处理:用独热编码替换
1 | # “Dummy_na=True”将“na”(缺失值)视为有效的特征值,并为其创建指示符特征 |
转换后将样本特征从79个增加到330个
通过values属性,可以从pandas格式中提取NumPy格式,并将其转换为张量表示用于训练
1 | n_train = train_data.shape[0] |
训练
训练一个带有均方损失的线性模型,一般来说将线性模型将作为基线(baseline)模型,直观地知道最好的模型有超出简单的模型多少
1 | loss = nn.MSELoss() |
房价就像股票价格一样,更关心的是相对误差$\frac{y - \hat{y}}{y}$而不是绝对误差
解决这个问题的一种方法是用价格预测的对数来衡量差异,事实上,这也是比赛中官方用来评价提交质量的误差指标
将$\mid\log y - \log \hat{y}\mid \leq \delta$ 转换为 $e^{-\delta} \leq \frac{\hat{y}}{y} \leq e^\delta$,使得预测价格的对数与真实标签价格的对数之间出现以下均方根误差RMSLE
$$
\sqrt{\frac{1}{n}\sum_{i=1}^n\left(\log y_i -\log \hat{y}_i\right)^2}
$$
1 | def log_rmse(net, features, labels): |
与前面的部分不同,训练函数将借助Adam优化器(后面讲),Adam优化器的主要吸引力在于它对初始学习率不那么敏感
1 | def train(net, train_features, train_labels, test_features, test_labels, |
K折交叉验证
K折交叉验证有助于模型选择和超参数调整
首先需要定义一个函数,在K折交叉验证过程中返回第$i$折的数据,具体来说就是它选择第$i$个切片作为验证数据,其余部分作为训练数据
这并不是处理数据的最有效方法,如果数据集大得多,完整地复制和拼接数据会带来显著的内存与计算开销
1 | def get_k_fold_data(k, i, X, y): |
在K折交叉验证中训练K次后,返回训练和验证误差的平均值
1 | def k_fold(k, X_train, y_train, num_epochs, lr, weight_decay, |
模型选择
找到合适的超参数通常需要较长时间,当数据量充足且超参数设置合理时,K 折交叉验证结果通常稳定
若超参数选择不当,验证误差可能失真,无法准确反映模型的真实性能
1 | k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64 |
这里为什么lr设的这么大呢?因为对输入特征值做了标准化,使得特征值较小,同时输出值房价较大,所以nn的权重都较大,所以学习率要相应较大才能加快收敛速度
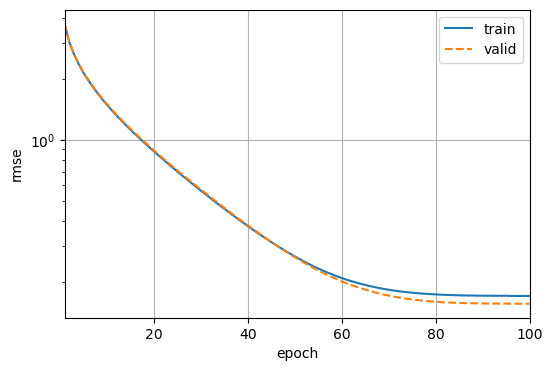
1 | 折 1: 训练 log RMSE = 0.1705, 验证 log RMSE = 0.1562 |
有时一组超参数的训练误差可能非常低,但K折交叉验证的误差要高得多,这表明模型过拟合了
提交Kaggle预测
使用所有数据对其进行训练,将预测保存在CSV文件中
1 | def train_and_pred(train_features, test_features, train_labels, test_data, |
1 | train_and_pred(train_features, test_features, train_labels, test_data, |
1 | 训练log rmse:0.162767 |
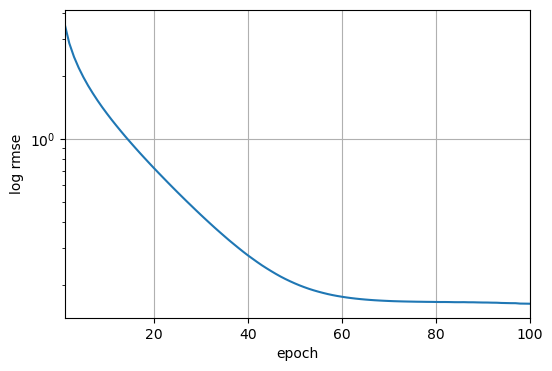
可以提交预测到Kaggle上,并查看在测试集上的预测与实际房价(标签)的比较情况
小结
- 真实数据通常混合了不同的数据类型,需要进行预处理
- 常用的预处理方法:将实值数据重新缩放为零均值和单位方法;用均值替换缺失值
- 将类别特征转化为指标特征,可以把这个特征当作一个独热向量来对待
- 可以使用折交叉验证来选择模型并调整超参数
- 对数对于相对误差很有用
当然,目前写的就是很简单的baseline,可优化空间非常多
思考题
用平均值替换缺失值总是好主意吗?
用平均值填补缺失只在缺失完全随机的情况下合理,若缺失模式与特征或标签有关(非随机缺失),平均值填补会掩盖数据结构、引入系统性偏差,让模型学到错误的统计关系


.webp)
 (1).png)