线性神经网络

从经典算法————线性神经网络开始，介绍神经网络的基础知识

经典统计学习技术中的线性回归和softmax回归可以视为线性神经网络

线性回归

基本元素

**回归(regression)**是能为一个或多个自变量与因变量之间关系建模的一类方法

在机器学习领域中的大多数任务通常都与**预测(prediction)**有关，但不是所有的预测都是回归问题

线性回归基于两个简单假设

• 自变量$\mathbf{x}$和因变量$y$之间的关系是线性的，即$y$可以表示为$\mathbf{x}$中元素的加权和，通常允许包含观测值的一些噪声
• 任何噪声都比较正常，如噪声遵循正态分布

为了开发一个能预测房价的模型，需要收集一个真实的数据集，包括房屋的销售价格、面积和房龄，该数据集称为训练集(training set)，每行数据称为样本(sample)

把试图预测的目标(房屋价格)称为标签(label)或目标(target)，预测所依据的自变量(面积和房龄)称为特征(feature)

通常使用$n$来表示数据集中的样本数，对索引为$i$的样本，其输入表示为$\mathbf{x}^{(i)} = [x_1^{(i)}, x_2^{(i)}]^\top$，其对应的标签是$y^{(i)}$

线性模型

根据线性假设，价格表示为
$$
\mathrm{price} = w_{\mathrm{area}} \cdot \mathrm{area} + w_{\mathrm{age}} \cdot \mathrm{age} + b.
$$
$w_{\mathrm{area}}$和$w_{\mathrm{age}}$称为权重，权重决定了每个特征对预测值的影响，$b$称为偏置(bias)

这个式子是输入特征的仿射变换(affine transformation)，即通过加权和对特征进行线性变换(linear transformation)，并通过偏置项来进行平移(translation)

给定一个数据集，目标是寻找模型的权重$\mathbf{w}$和偏置$b$

输入包含$d$个特征时，将预测结果$\hat{y}$表示为
$$
\hat{y} = w_1 x_1 + … + w_d x_d + b.
$$
将所有特征放到向量$\mathbf{x} \in \mathbb{R}^d$，并将所有权重放到向量$\mathbf{w} \in \mathbb{R}^d$中，可以用点积形式来简洁地表达模型
$$
\hat{y} = \mathbf{w}^\top \mathbf{x} + b.
$$
用矩阵$\mathbf{X} \in \mathbb{R}^{n \times d}$可以很方便地引用整个数据集的$n$个样本，每一行是一个样本，每一列是一种特征

预测值$\hat{\mathbf{y}} \in \mathbb{R}^n$通过矩阵-向量乘法表示为
$$
\color{purple} {\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b
$$
无论使用什么手段来观察特征$\mathbf{X}$和标签$\mathbf{y}$都可能会出现少量的观测误差

因此即使确信特征与标签的潜在关系是线性的，也会加入一个噪声项来考虑观测误差带来的影响

在开始寻找最好的模型参数$\mathbf{w}$和$b$之前，需要确定两项

• 模型质量的度量方式
• 能够更新模型以提高模型预测质量的方法

损失函数

**损失函数(loss function)**能够量化目标的实际值与预测值之间的差距，通常选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0

回归问题中最常用的损失函数是均方误差函数，样本$i$的预测值为$\hat{y}^{(i)}$，其真实标签为$y^{(i)}$时，平方误差表示为
$$
l^{(i)}(\mathbf{w}, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2.
$$
常数1/2不会带来本质的差别，但这样方便后续求导

计算在训练集$n$个样本上的均方误差
$$
L(\mathbf{w}, b) =\frac{1}{n}\sum_{i=1}^n l^{(i)}(\mathbf{w}, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2=\frac{1}{n}\mid\mid \mathbf y-\mathbf X \mathbf w\mid\mid^2
$$

解析解

线性回归的解可以用一个公式简单地表达出来，这类解叫作解析解(analytical solution)

可以直接通过代数公式求出最优解，不需要迭代算法(如梯度下降)

将损失关于$\mathbf{w}$的导数设为0，得到解析解

计算过程

1. 先把损失函数展开
   $$
   L(\mathbf w,b)=(\mathbf y-\mathbf X \mathbf w)^{\top}(\mathbf y-\mathbf X \mathbf w)
   $$

2. 对$\mathbf w$求导，并令导数为零(最小值点的一阶导数为零)
   $$
   \frac{\partial L}{\partial \mathbf w}=-2 \mathbf X^{\top}(\mathbf y-\mathbf X \mathbf w)=0
   $$

3. 移项得
   $$
   \mathbf X^{\top} \mathbf X \mathbf w=\mathbf X^{\top} \mathbf y
   $$

4. 当$\mathbf X^{\top} \mathbf X $ 可逆时，求得解析解
   $$
   \mathbf{w}^* = (\mathbf X^\top \mathbf X)^{-1}\mathbf X^\top \mathbf{y}.
   $$

但并不是所有的问题都存在解析解

解析解对问题的限制很严格，导致它无法广泛应用在深度学习里

随机梯度下降SGD

随机梯度下降SGD几乎可以优化所有深度学习模型，它通过在损失函数递减的方向上更新参数来降低误差

最简单的用法是计算损失函数关于模型参数的导数，但计算量可能很大，通常会随机抽取一小批样本，这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)

在每次迭代中，首先随机抽样一个小批量，由批量大小(batch size)为$\mid \mathcal{B}\mid $个的训练样本组成的，计算平均损失关于模型参数的导数，将梯度乘以学习率$\eta$(learning rate)，并从当前参数的值中减掉
$$
(\mathbf{w},b) \leftarrow (\mathbf{w},b) - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{(\mathbf{w},b)} l^{(i)}(\mathbf{w},b).
$$
使得参数沿着让误差变小的方向移动

算法的步骤如下：

1. 初始化模型参数的值，如随机初始化
2. 从数据集中随机抽取小批量样本且在负梯度的方向上更新参数，并不断迭代

对于均方损失和仿射变换可以写成
$$
\begin{split}\begin{aligned} \mathbf{w} &\leftarrow \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_{\mathbf{w}} l^{(i)}(\mathbf{w}, b) = \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right),\\
b &\leftarrow b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \partial_b l^{(i)}(\mathbf{w}, b) = b - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned}\end{split}
$$
批量大小和学习率的值通常是手动预先指定，而不是通过模型训练得到的

可以调整但不在训练过程中更新的参数称为超参数(hyperparameter)，调参是选择超参数的过程

超参数通常是根据训练迭代结果来调整的，而训练迭代结果是在独立的**验证数据集(validation dataset)**上评估得到的

线性回归是在整个域中只有一个最小值的学习问题，但是对像深度神经网络这样复杂的模型来说，损失平面上通常包含多个最小值。更难做到的是找到一组参数，这组参数能够在从未见过的数据上实现较低的损失，这一挑战被称为泛化(generalization)

矢量化加速

训练模型时，经常希望能够同时处理整个小批量的样本，为了实现这一点，需要对计算进行矢量化， 从而利用线性代数库，而不是在Python中编写开销高昂的for循环

因为频繁对运行时间进行基准测试，需要定义一个计时器类

import time
import numpy as np
class Timer:  #@save
    """记录多次运行时间"""
    def __init__(self):
        self.times = [] # 保存每次运行的耗时
        self.start()    # 初始化时就自动调用start()

    def start(self):
        """启动计时器"""
        self.tik = time.time()

    def stop(self):
        """停止计时器并将时间记录在列表中"""
        self.times.append(time.time() - self.tik)
        return self.times[-1]

    def avg(self):
        """返回平均时间"""
        return sum(self.times) / len(self.times)

    def sum(self):
        """返回时间总和"""
        return sum(self.times)

    def cumsum(self):
        """返回累计时间"""
        return np.array(self.times).cumsum().tolist()

现在可以对工作负载进行基准测试

使用for循环，每次执行一位的加法

n = 10000
a = torch.ones(n)
b = torch.ones(n)
c = torch.zeros(n)
timer = Timer()
for i in range(n):
    c[i] = a[i] + b[i]
f'{timer.stop():.5f} sec'
# 输出'0.06851 sec'

使用重载的+运算符来计算按元素的和

timer.start()
d = a + b
f'{timer.stop():.5f} sec'
# 输出'0.00000 sec'

矢量化代码通常会带来数量级的加速

正态分布与平方损失

正态分布(normal distribution)也称为高斯分布(Gaussian distribution)，和线性回归之间的关系很密切

若随机变量$x$具有均值$\mu$和方差$\sigma^2$，其正态分布概率密度函数如下
$$
p(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (x - \mu)^2\right).
$$

def normal(x, mu, sigma):
    p = 1 / np.sqrt(2 * np.pi * sigma**2)
    return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)
x = np.arange(-7, 7, 0.01)
params = [(0, 1), (0, 2), (3, 1)]
for mu, sigma in params:
    plt.plot(x, normal(x, mu, sigma), label=f'$\mu$={mu}, $\sigma$={sigma}')
plt.xlabel('x')
plt.ylabel('p(x)')
plt.grid()
plt.legend()

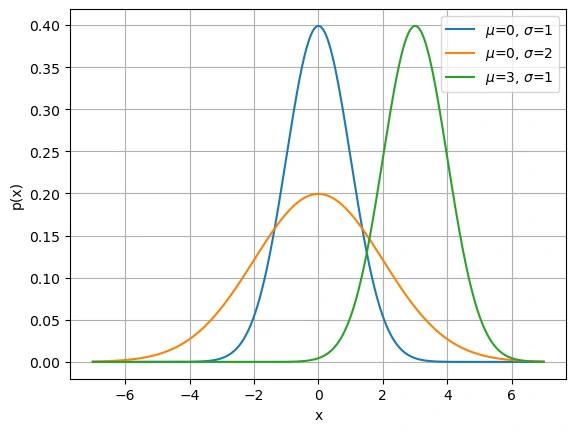
改变均值会产生沿轴的偏移，增加方差将会分散分布、降低其峰值

假设了观测中包含噪声，其中噪声服从正态分布$\epsilon \sim \mathcal{N}(0, \sigma^2)$
$$
y = \mathbf{w}^\top \mathbf{x} + b + \epsilon
$$
通过给定的$\mathbf{x}$观测到特定$y$的似然(likelihood)
$$
P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right).
$$
根据极大似然估计法(MLE)，参数$\mathbf{w}$和$b$的最优值是使整个数据集似然最大的值
$$
P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}).
$$
由于历史原因，优化通常是说最小化而不是最大化，所以改为最小化负对数似然$-\log P(\mathbf y \mid \mathbf X)$

$$
-\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2
$$
第一项与$\mathbf{w},b$无关；第二项除了系数，其余部分与平方方误差相同，所以在高斯噪声的假设下，最小化平方误差等价于对线性模型的极大似然估计

从线性回归到深度网络

将线性回归模型描述为一个神经网络

该图只显示连接模式，即只显示每个输入如何连接到输出，隐去了权重和偏置的值

由于模型重点在发生计算的地方，所以通常在计算层数时不考虑输入层，图中神经网络的层数为1

可以将线性回归模型视为仅由单个人工神经元组成的神经网络，或称为单层神经网络

对于线性回归，每个输入都与每个输出相连，将这种变换(图中输出层)称为全连接层(fully-connected layer)

练习题

1. 假设有一些数据$x_1, \ldots, x_n \in \mathbb{R}$，目标是找到一个常数$b$，使最小化$\sum_i (x_i - b)^2$

   • 找到最优值$b$的解析解
   • 这个问题及其解与正态分布有什么关系

   $$
   \begin{aligned}
   &f^{\prime}(b)=\sum_{i=1}^n 2\left(b-x_i\right)=2\left(n b-\sum_i x_i\right)=0 \Rightarrow b^*=\frac{1}{n} \sum_{i=1}^n x_i=\bar{x} .
   \end{aligned}
   $$

   二阶导$f^{\prime \prime}(b)=2 n>0$，因此这是唯一全局最小值

   所以最小二乘下，最优常数就是样本均值

   若数据独立同分布于$\mathcal{N}(\mu , \sigma^2)$，极大化似然就等价于最小化平方和，因此MLE的$\mu$就是$\bar x$，这解释了为什么“最小二乘”天然匹配“高斯噪声”

   如果把损失从$L_2$改为$L_1$范数，最优常数会变成中位数

2. 用矩阵和向量表示法写出优化问题

   带上偏置$b$的写法
   $$
   \tilde {\mathbf X} = [\mathbf X \quad \mathbf 1] \in \mathbb{R}^{n\times (d+1)},\tilde {\mathbf w} = [\mathbf w^\top\quad b]^\top
   $$

3. 损失对$w$的梯度
   $$
   \nabla_{\mathbf w} L=-2 \mathbf X^{\top}(\mathbf y-\mathbf X \mathbf w) \rightarrow \nabla^2_{\mathbf w} L = 2\mathbf X^{\top} \mathbf X
   $$
   二阶导数大于等于0

4. 什么时候使用随机梯度下降更好？这种方法何时会失效？

   样本数量大，特征维度也大时使用随机梯度下降更好，深度神经网络训练几乎都是用 SGD 及其变种

   学习率/调度不当，损失函数过于崎岖时将失效

5. 假定控制附加噪声的噪声模型是指数分布$p(\epsilon) = \frac{1}{2} \exp(-|\epsilon|)$

   • 写出模型$-\log P(\mathbf y \mid \mathbf X)$下数据的负对数似然
     $$
     P(y \mid \mathbf{x}) = \frac{1}{2}\exp (-\mid y - \mathbf{w}^\top \mathbf{x} - b \mid)
     $$
     负对数似然
     $$
     -\log P(\mathbf y \mid \mathbf X) = n\log2 + \sum_{i=1}^n\mid y - \mathbf{w}^\top \mathbf{x} - b \mid
     $$
     常数项忽略以后等价于最小化 L1 回归损失

   • 提出一种随机梯度下降算法来解决这个问题。哪里可能出错？

     L1 在 0 处有“拐点”，$\operatorname{sgn}(r)$会在正负之间反复切换，如果学习率不衰减就会持续震荡，导致无法收敛

线性回归的底层实现

虽然深度学习框架几乎可以自动化地进行所有这些工作，但从零开始实现可以确保知道自己在做什么

生成数据集

将根据带有噪声的线性模型构造一个数据集，合成数据集是一个矩阵$\mathbf{X}\in \mathbb{R}^{1000 \times 2}$

使用线性模型参数$\mathbf{w} = [2, -3.4]^\top$，$b = 4.2$以及噪声$\varepsilon $生成数据集及其标签

$\epsilon$可以视为模型预测和标签时的潜在观测误差，假设服从均值为0的正态分布，标准差为0.01

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))
    y = torch.matmul(X, w) + b # 等价于 X @ w + b，在高维推荐matmul
    y += torch.normal(0, 0.01, y.shape)
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)

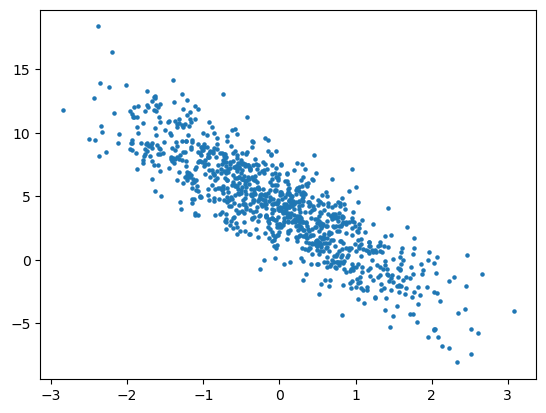
通过生成第二个特征features[:, 1]和labels的散点图，可以直观观察到两者之间的线性关系

# 需要从张量换为numpy
plt.scatter(features[:,1].detach().numpy(), labels.detach().numpy(),s=5)
plt.show()

读取数据集

训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新模型

有必要定义一个函数，该函数能打乱数据集中的样本并以小批量方式获取数据

定义一个data_iter函数，该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量，每个小批量包含一组特征和标签

import random
def data_iter(batch_size, features, labels):
    num_examples = len(features) # 统计样本数
    indices = list(range(num_examples)) # 创建索引列表
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)  # 打乱索引顺序
    for i in range(0, num_examples, batch_size): # 遍历样本
        # 获得按batch_size大小获取随机索引
        batch_indices = torch.tensor(  # 张量索引为了减少隐式拷贝
            indices[i: min(i + batch_size, num_examples)]) 
        yield features[batch_indices], labels[batch_indices] # 逐次返回

利用GPU并行运算的优势，处理合理大小的“小批量”

每个样本都可以并行地进行模型计算，且每个样本损失函数的梯度也可以被并行计算

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

当运行迭代时，会连续地获得不同的小批量，直至遍历完整个数据集

但这种迭代的执行效率很低，因为需要把所有数据读入，并且执行大量的随机内存访问

在深度学习框架中实现的内置迭代器效率要高得多，它可以处理存储在文件中的数据和数据流提供的数据

初始化模型参数

通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重，并将偏置初始化为0

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

之后更新这些参数，直到这些参数足够拟合数据，每次更新都需要计算损失函数关于模型参数的梯度，有了这个梯度，就可以向减小损失的方向更新每个参数

根据之前引入的自动微分来计算梯度(requires_grad=True)

定义模型

将模型的输入和参数同模型的输出关联起来

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

定义损失函数

定义损失函数是重中之重，这里使用之前描述的平方损失函数

需要将真实值y的形状转换为和预测值y_hat的形状相同

def squared_loss(y_hat, y):  #@save
    """平方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
    # 这里reshape是为了避免出现广播 

定义优化算法

线性回归有解析解，但其实大部分模型是没有解析解的，这里利用小批量梯度下降

使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度，朝着减少损失的方向更新参数，该函数接受模型参数集合、学习速率和批量大小作为输入

• 每一步更新的大小由学习速率lr决定
• 计算的损失是一个批量样本的总和，用批量大小(batch_size)来规范化步长

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad(): # 以下操作不追踪梯度，优化步骤常用
        for param in params:
            # param.grad PyTorch 自动计算得到的梯度
            param -= lr * param.grad / batch_size
            param.grad.zero_()  # 清除梯度累积，结尾 _ 表示这是原地操作

训练

已经准备好了模型训练所有需要的要素，可以实现主要的训练过程部分了

将执行以下循环：

• 初始化参数
• 重复以下训练，直到完成
  1. 计算梯度$\mathbf{g} \leftarrow \partial_{(\mathbf{w},b)} \frac{1}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} l(\mathbf{x}^{(i)}, y^{(i)}, \mathbf{w}, b)$
  2. 更新参数$(\mathbf{w}, b) \leftarrow (\mathbf{w}, b) - \eta \mathbf{g}$

在每个迭代周期(epoch)中，使用data_iter函数遍历整个数据集，并将训练数据集中所有样本都使用一次(假设样本数能够被批量大小整除)

在该例子中迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03

设置超参数很棘手，需要通过反复试验进行调整

lr = 0.03         # 学习率
num_epochs = 3    # 迭代次数
batch_size = 10   # 小样本数
net = linreg      # 模型函数(线性回归 y = Xw + b)
loss = squared_loss   # 损失函数(平方损失)
# 初始化随机参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True) 
b = torch.zeros(1, requires_grad=True)
# 根据真实参数创建含噪样本
features, labels = synthetic_data(true_w, true_b, 1000)

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y) # net前向传播，计算预测值
        l.sum().backward()
        # 因为l形状是(batch_size,1)，而不是一个标量
        # l中的所有元素被加到一起，并以此计算关于[w,b]的梯度
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad(): # 性能评估不追踪梯度
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

输出

epoch 1, loss 0.025137
epoch 2, loss 0.000085
epoch 3, loss 0.000046

对比之前设置的真实参数

print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

w的估计误差: tensor([1.0513e-03, 6.3181e-05], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0004], grad_fn=<RsubBackward1>)

在机器学习中，通常不太关心恢复真正的参数，而更关心如何高度准确预测参数

即使是在复杂的优化问题上，随机梯度下降通常也能找到非常好的解，因为在深度网络中存在许多参数组合能够实现高度精确的预测

练习题

1. 如果将权重初始化为零，会发生什么，算法仍然有效吗？

   像线性回归这种问题，因为损失函数是凸函数，梯度在所有方向上都是对称的，不管初始点在哪，梯度下降都会沿着唯一方向走到全局最优

   但在神经网络这种多层模型里就不行了，如果权重都初始化为0，那么所有的神经元都一样，梯度也完全一样，就会出现对称性问题，陷入死局

   模型类型	全零初始化后果	原因
   线性回归	可行	损失函数是凸的，无对称问题
   逻辑回归	可行	一层模型，不存在多通道对称性
   神经网络(多层)	失败	神经元对称、梯度相同、学习停滞

2. 计算二阶导数时可能会遇到什么问题？这些问题可以如何解决？

   只在第一次求导时指定 create_graph=True，PyTorch 才会保留梯度计算图，从而允许继续求导

   x = torch.tensor(4.0, requires_grad=True)
   y = x ** 3
   y.backward(create_graph=True) # 保留梯度计算图
   print(x.grad) # 输出48 3x^2=48符合
   grad_x = x.grad.clone() # 不能"="，只是赋地址，grad.zero_()清掉了
   x.grad.zero_() # 避免梯度累加，因为我只看二阶导梯度
   grad_x.backward() # 再次反向传播
   print(x.grad)

3. 为什么在squared_loss函数中需要使用reshape函数？

   y_hat的形状可能是 (batch_size, 1) 或 (batch_size,)

   y的形状常常是 (batch_size,)

   如果直接计算可能会出现广播机制

   y_hat.shape = (3, 1)
   y.shape     = (3,)

   广播后变为(3,3)的矩阵计算，这肯定是不对的

   显式地让 y 的形状与 y_hat 完全一致，确保预测值和真实值形状一致，从而进行逐元素平方损失计算

4. 尝试使用不同的学习率，观察损失函数值下降的快慢

   学习率越大，损失函数下降越快

5. 如果样本个数不能被批量大小整除，data_iter函数的行为会有什么变化？

   情况	优点	缺点
   保留不满批次	所有样本都用上	最后一批大小不一致，梯度波动略大
   丢弃不满批次	批次形状一致，利于并行	一部分样本没被训练

线性回归的简洁实现

由于数据迭代器、损失函数、优化器和神经网络层很常用，现代深度学习库已经实现了这些组件

生成数据集一般没有特殊的封装函数，毕竟大部分情况下数据都是已经获取好，读入即可

读取数据集

可以调用PyTorch框架中现有的API来读取数据，将features和labels作为API的参数传递

from torch.utils import data
def load_array(data_arrays, batch_size, is_train=True):
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)
batch_size = 10
data_iter = load_array((features,labels), batch_size, True)

定义模型

对于标准深度学习模型，可以使用框架的预定义好的层，只需关注使用哪些层来构造模型，而不必关注层的实现细节

首先定义一个模型变量net，它是一个Sequential类的实例

Sequential类将多个层串联在一起，当给定输入数据时，Sequential实例将数据传入到第一层，然后将第一层的输出作为第二层的输入，以此类推

当前单层连接所有输入，所以为全连接层

在PyTorch中，全连接层在Linear类中定义，将两个参数传递到nn.Linear中

• 参数1指定输入特征形状，即2

• 参数2指定输出特征形状，输出特征形状为单个标量，因此为1

from torch import nn
net = nn.Sequential(nn.Linear(2, 1))

初始化模型参数

在使用net之前，需要初始化模型参数，如在线性回归模型中的权重和偏置

深度学习框架通常有预定义的方法来初始化参数

在这里指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样，偏置参数将初始化为零

通过net[0]选择网络中的第一个图层，然后使用weight.data和bias.data方法访问参数，还可以使用替换方法normal_和fill_来重写参数值

net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

定义损失函数

计算均方损失使用的是MSELoss类，也称为均方$L_2$范数

loss = nn.MSELoss(reduction='mean')

参数reduction

• 默认mean，对所有元素的损失取平均值，最常用，标准化损失
• none，不进行任何聚合，返回与输入相同形状的逐元素损失
• sum，对所有元素的损失求和，希望损失值与样本规模成比例，常出现于最大似然

定义优化算法

小批量随机梯度下降算法是一种优化神经网络的标准工具，PyTorch在optim模块中实现了该算法的许多变种

当实例化一个SGD实例时，要指定优化的参数(可通过net.parameters()从模型中获得)以及优化算法所需的超参数字典

小批量随机梯度下降只需要设置lr值，这里设置为0.03

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

训练

通过深度学习框架的高级API来实现，只需要相对较少的代码

不必单独分配参数、不必定义损失函数，也不必手动实现小批量随机梯度下降

当有了所有的基本组件，训练过程代码与从零开始实现时所做的非常相似

对于每一个小批量，会进行以下步骤

1. 通过调用net(X)生成预测并计算损失l(前向传播)
2. 通过进行反向传播来计算梯度
3. 通过调用优化器来更新模型参数

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y)
        trainer.zero_grad() # 在每个 batch 训练前清空上一次的梯度
        l.backward()        # 反向传播，自动计算损失 l 对所有参数的梯度
        # 如果要访问参数的梯度
        # net.weight.grad
        # net.bias.grad
        trainer.step()      # 根据刚刚算出的梯度，更新模型参数
    # 在每个 epoch 结束后，重新计算整个数据集上的损失
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

输出

epoch 1, loss 0.000252
epoch 2, loss 0.000100
epoch 3, loss 0.000102

访问训练出的权重和偏置

w = net[0].weight.data
print('w的估计误差：', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差：', true_b - b)

w的估计误差： tensor([0.0014, 0.0002])
b的估计误差： tensor([0.0005])

内置函数

所有损失函数都在 torch.nn 中实现为类

初始化方法位于 torch.nn.init 模块中

回归问题的损失函数：

损失函数	说明	默认公式
nn.MSELoss()	均方误差(Mean Squared Error)	$\frac{1}{n}\sum(y - \hat{y})^2$
nn.L1Loss()	平均绝对误差(Mean Absolute Error)	$\frac{1}{n}\sum\mid y- \hat y \mid $
nn.SmoothL1Loss()	平滑版 L1，融合 L1 与 L2 优点	对小误差用平方 大误差用绝对值
nn.HuberLoss()	类似 SmoothL1，可设阈值 δ 控制	兼顾稳健性与可导性

权重初始化方法：

常规初始化

import torch.nn.init as init
init.constant_(tensor, val)       # 所有元素设为常数
init.zeros_(tensor)               # 全零
init.ones_(tensor)                # 全一
init.uniform_(tensor, a, b)       # 均匀分布 U(a, b)
init.normal_(tensor, mean, std)   # 正态分布 N(mean, std)

Xavier(Glorot)初始化

保持前后层的方差一致，防止梯度消失或爆炸，常用于 Sigmoid 或 tanh 激活

init.xavier_uniform_(tensor)
init.xavier_normal_(tensor)

Kaiming(He)初始化

适用于 ReLU 或 LeakyReLU 激活函数

init.kaiming_uniform_(tensor, nonlinearity='relu')
init.kaiming_normal_(tensor, nonlinearity='relu')

正交初始化

保持权重矩阵的正交性，广泛用于循环神经网络(RNN/LSTM)，可以避免梯度爆炸

init.orthogonal_(tensor)

稀疏初始化

让部分连接为0，适合稀疏神经网络

init.sparse_(tensor, sparsity=0.1)

小结

• 在PyTorch中，data模块提供了数据处理工具，nn模块定义了大量的神经网络层和常见损失函数
• 可以通过_结尾的方法将参数替换，从而初始化参数

softmax回归的概念

分类这个词可描述两个有微妙差别的问题：

1. 只对样本的“硬性”类别感兴趣，即属于哪个类别
2. 希望得到“软性”类别，即得到属于每个类别的概率

这两者的界限往往很模糊，因为即使只关心硬类别，仍然使用软类别的模型

分类问题

从一个图像分类问题开始，假设每次输入是一个$2\times 2$的灰度图像，可以用一个标量表示每个像素值，每个图像对应四个特征$x_1, x_2, x_3, x_4$，假设每个图像属于类别“猫”“鸡”和“狗”中的一个

接下来要考虑如何表示标签，最直接的想法是选择$y \in {1, 2, 3}$来分别表示${\text{狗}, \text{猫}, \text{鸡}}$，这是在计算机上存储此类信息的有效方法，但这种方法需要类别间有一些自然顺序

但是一般的分类问题并不与类别之间的自然顺序有关，所以需要利用独热编码(one-hot encoding)

独热编码是一个向量，它的分量和类别一样多，类别对应的分量设置为1，其他所有分量设置为0

在例子中，标签$y$将是一个三维向量，其中$(1, 0, 0)$对应于“猫”、$(0, 1, 0)$对应于“鸡”、$(0, 0, 1)$对应于“狗”
$$
y \in {(1, 0, 0), (0, 1, 0), (0, 0, 1)}.
$$

网络架构

为了估计所有可能类别的条件概率，需要一个有多个输出的模型，每个类别对应一个输出

为了解决线性模型的分类问题，需要和输出一样多的仿射函数，每个输出对应于它自己的仿射函数

回到简单例子中，有4个特征和3个可能的输出类别，将需要12个标量来表示权重(带下标的$w$)，3个标量来表示偏置(带下标的$b$)

为每个输入计算三个未规范化的预测
$$
\begin{split}\begin{aligned}
o_1 &= x_1 w_{11} + x_2 w_{12} + x_3 w_{13} + x_4 w_{14} + b_1,\\
o_2 &= x_1 w_{21} + x_2 w_{22} + x_3 w_{23} + x_4 w_{24} + b_2,\\
o_3 &= x_1 w_{31} + x_2 w_{32} + x_3 w_{33} + x_4 w_{34} + b_3.
\end{aligned}\end{split}
$$
和线性回归一样，softmax回归也是一个单层神经网络且输出层也是全连接层

为了更简洁地表达模型，仍然使用线性代数符号，通过向量形式表达为$\mathbf{o} = \mathbf{W} \mathbf{x} + \mathbf{b}$

权重在一个$3 \times 4$的矩阵中，对于给定数据样本的特征$\mathbf{x}$，输出是由权重与输入特征进行矩阵-向量乘法再加上偏置得到的

全连接层的参数开销

在深度学习中，全连接层无处不在，但是全连接层可能有很多可学习的参数

对于任何具有$d$个输入和$q$个输出的全连接层，参数开销为$\mathcal{O}(dq)$，但通过低秩分解将矩阵拆分，引入一个中间的低维隐空间，用较少的参数去近似原始映射

此时参数数量从$dq$下降为$dn+nq=O(\frac{dq}{n})$(当$n\ll d,q$时)

其中超参数$n$可以灵活指定，但是需要平衡参数节约和模型有效性

softmax运算

为了得到预测结果将设置一个阈值，如选择具有最大概率的标签

希望模型的输出$\hat{y}_j$可以视为属于类$j$的概率，然后选择具有最大输出值的类别$\operatorname*{argmax}_j y_j$作为预测

能否将未规范化的预测$o$直接视作我们感兴趣的输出呢？这肯定是不行的，将线性层的输出直接视为概率时存在一些问题：

• 没有限制输出总和为1
• 根据输入不同，输出可能为负值

这已经违反了概率基本公理

要将输出视为概率，必须保证在任何数据上的输出都是非负的且总和为1

此外，需要一个训练的目标函数，来激励模型精准地估计概率

比如在分类器输出0.5的所有样本中，希望这些样本是刚好有一半实际上属于预测的类别，这个属性叫做校准(calibration)

在选择模型理论基础上发明的softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质

首先对每个未规范化的预测求幂(这样可以确保输出非负)，再让每个求幂后的结果除以它们的总和
$$
\hat{\mathbf{y}} = \mathrm{softmax}(\mathbf{o})\quad \text{其中}\quad \hat{y}_j = \frac{\exp(o_j)}{\sum_k \exp(o_k)}
$$
这样$\hat{\mathbf{y}}$可以视为一个正确的概率分布

softmax运算不会改变未规范化的预测之间的大小次序，只会确定分配给每个类别的概率，所以仍然可以用下式来选择最有可能的类别
$$
\operatorname*{argmax}_j \hat y_j = \operatorname*{argmax}_j o_j.
$$

小批量样本的矢量化

假设读取了一个批量的样本$\mathbf{X}$，其中特征维度(输入数量)为$d$，批量大小为$n$，并假设在输出中有$q$个类别

那么小批量样本的特征为$\mathbf{X} \in \mathbb{R}^{n \times d}$，权重为$\mathbf{W} \in \mathbb{R}^{d \times q}$，偏置为$\mathbf{b} \in \mathbb{R}^{1\times q}$

softmax回归的矢量计算表达式为：
$$
\begin{split}\begin{aligned} \mathbf{O} &= \mathbf{X} \mathbf{W} + \mathbf{b}, \\ \hat{\mathbf{Y}} & = \mathrm{softmax}(\mathbf{O}). \end{aligned}\end{split}
$$
相对于一次处理一个样本，小批量样本的矢量化加快了$\mathbf{X},\mathbf{W}$的矩阵-向量乘法

由于$\mathbf{X}$中的每一行代表一个数据样本，那么softmax运算可以按行执行

这里的偏置依旧会触发广播机制，小批量的未规范化预测$\mathbf{O}$和输出概率$\hat{\mathbf{Y}}$都是形状为$n \times q$的矩阵

损失函数

需要一个损失函数来度量预测的效果，将使用最大似然估计，这与在线性回归中的方法相同

对数似然

softmax函数给出了一个向量$\hat{\mathbf{y}}$，可以将其视为“对给定任意输入$\mathbf{x}$的每个类的条件概率”

假设整个数据集${\mathbf{X}, \mathbf{Y}}$具有$n$个样本，其中索引$i$的样本由特征向量$\mathbf{x}^{(i)}$和独热标签向量$\mathbf{y}^{(i)}$组成

可以将估计值与实际值进行比较
$$
P(\mathbf{Y} \mid \mathbf{X}) = \prod_{i=1}^n P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)}).
$$
根据最大似然估计，最大化$P(\mathbf{Y} \mid \mathbf{X})$相当于最小化负对数似然
$$
-\log P(\mathbf{Y} \mid \mathbf{X}) = \sum_{i=1}^n -\log P(\mathbf{y}^{(i)} \mid \mathbf{x}^{(i)})
= \sum_{i=1}^n l(\mathbf{y}^{(i)}, \hat{\mathbf{y}}^{(i)}),
$$
其中，对于任何标签$\mathbf{y}$和模型预测$\hat{\mathbf{y}}$，损失函数为
$$
l(\mathbf{y}, \hat{\mathbf{y}}) = - \sum_{j=1}^q y_j \log \hat{y}_j.
$$
通常被称为交叉熵损失(cross-entropy loss)

• 由于$\mathbf{y}$是一个长度为$q$的独热编码向量，所以除了一个项以外的所有项$j$都消失了
• 由于所有$\hat{y}_j$都是预测的概率，所以对数永远不会大于0

如果正确预测实际标签，即$P(\mathbf{y} \mid \mathbf{x})=1$，则损失函数不能进一步最小化，但是基本不会出现

因为数据集中可能存在标签噪声(比如某些样本可能被误标)

softmax及其导数

利用softmax的定义得到
$$
\begin{split}\begin{aligned}
l(\mathbf{y}, \hat{\mathbf{y}}) &= - \sum_{j=1}^q y_j \log \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} \\
&= \sum_{j=1}^q y_j \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j\\
&= \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j.
\end{aligned}\end{split}
$$
考虑相对于任何未规范化的预测$o_j$的导数得到
$$
\partial_{o_j} l(\mathbf{y}, \hat{\mathbf{y}}) = \frac{\exp(o_j)}{\sum_{k=1}^q \exp(o_k)} - y_j = \mathrm{softmax}(\mathbf{o})_j - y_j = \hat y_j-y_j
$$
发现导数是softmax模型分配的概率与实际发生的情况(由独热标签向量表示)之间的差异

这与之前在回归中看到的非常相似，其中梯度是观测值与预估值之间的差异

这不是巧合，在任何指数族分布模型中，对数似然的梯度正是由此得出的

交叉熵损失

对于标签$\mathbf{y}$可以使用与以前相同的表示形式，唯一的区别是现在用一个概率向量表示，而不是仅包含二元项的向量

使用交叉熵来定义损失
$$
\begin{align*}
l(\mathbf{y}, \hat{\mathbf{y}})
= -\sum_{j=1}^q y_j \log \hat y_j
= \log \sum_{k=1}^q \exp(o_k) - \sum_{j=1}^q y_j o_j
\end{align*}
$$
它是所有标签分布的预期损失值，是分类问题最常用的损失之一

从信息论看交叉熵

熵

信息论的核心思想是量化数据中的信息内容，该数值被称为分布的熵(entropy)
$$
H[P] = \sum_j - P(j) \log P(j).
$$
信息论的基本定理之一指出，为了对从分布$p$中随机抽取的数据进行编码，至少需要“$H[P]$纳特(nat)”对其进行编码

注意，这里的 “纳特”相当于比特(bit)，但是对数底为$e$而非2，1纳特约为1.44比特
$$
\frac{1}{\log(2)} \approx 1.44
$$

信息量

如果一个数据流很容易预测，那它就很容易压缩

信息量小 = 可预测性强 = 可压缩性高

如果不能完全预测每一个事件，有时可能会感到“惊异”，克劳德·香农决定用信息量来量化这种惊异程度

$$
\log \frac{1}{P(j)} = -\log P(j)
$$
在观察一个事件$j$时赋予它主观概率$P(j)$，概率越低惊异会更大，该事件的信息量也就更大

当考虑所有可能事件时，信息量的期望就是熵

再看交叉熵

可以把交叉熵想象为“主观概率为$Q$的观察者在看到根据概率$P$生成的数据时的预期惊异”

当$P=Q$时，交叉熵达到最低，在这种情况下，从$P$到$Q$的交叉熵是$H(P, P)= H(P)$，没有额外的惊讶

可以从两方面来考虑交叉熵分类目标：

1. 最大化观测数据的似然
2. 最小化传达标签所需的惊异(压缩)

练习题

计算softmax交叉熵损失的二阶导数，并计算$\mathrm{softmax}(\mathbf{o})$给出的分布方差，并与上面计算的二阶导数匹配

对梯度再求一次导得到
$$
\frac{\partial^2 l}{\partial o_i \partial o_j}=\frac{\partial}{\partial o_j}\left(\hat y_i-y_i\right)=\frac{\partial \hat y_i}{\partial o_j}
$$
Softmax的导数公式是
$$
\frac{\partial \hat y_i}{\partial o_j}=\hat y_i\left(\delta_{i j}-\hat y_j\right)
$$
所以二阶导矩阵(Hessian)为
$$
H_{i j}=\hat y_i\left(\delta_{i j}-\hat y_j\right)
$$
即
$$
H=\operatorname{diag}(\hat{\mathbf{y}})-\hat{\mathbf{y}} \hat{\mathbf{y}}^{\top}
$$
对于一个类别分布(多项分布)的协方差
$$
\operatorname{Cov}[\hat{\mathbf{y}}]=\operatorname{diag}(\hat{\mathbf{y}})-\hat{\mathbf{y}} \hat{\mathbf{y}}^{\top}
$$
会发现这正好和上面的 Hessian 完全一样！

图像分类数据集

MNIST数据集(LeCun et al., 1998)是图像分类中广泛使用的数据集之一，但作为基准数据集过于简单，将使用类似但更复杂的Fashion-MNIST数据集 (Xiao et al., 2017)

Fashion-MNIST由10个类别的图像组成，每个类别由训练数据集中的6000张图像和测试数据集中的1000张图像组成，因此训练集和测试集分别包含60000和10000张图像

先导入一部分包

import torch
import torchvision # 图像数据 + 图像模型 + 图像处理
from torch.utils import data # 数据加载接口
from torchvision import transforms # 图像数据预处理与增强

常用数据集

分类任务数据集(Image Classification)

数据集名称	用途
MNIST	手写数字识别，灰度图(28×28)
FashionMNIST	服装分类任务，灰度图(28×28)
CIFAR10	10类彩色小图(32×32)，经典视觉分类
CIFAR100	CIFAR10 的扩展(100 类)
ImageNet	大规模分类基准，1000 类
STL10	类似 CIFAR，但图像更高分辨率(96×96)
SVHN	街景数字识别(彩色数字)
Caltech101 / 256	多种物体类别图像

读取数据集

可以通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中

trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
    root="data", train=False, transform=trans, download=True)

transforms.ToTensor()：把一张PIL图片(NumPy数组)转换成张量(Tensor)，并把像素值从[0, 255]映射到[0, 1]之间，图像的维度从(H, W, C)变为(C, H, W)

mnist_train[0][0].shape # torch.Size([1, 28, 28])

Fashion-MNIST中包含的10个类别，以下函数用于在数字标签索引及其文本名称之间进行转换

def get_fashion_mnist_labels(labels):  #@save
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

现在可以创建一个函数来可视化这些样本

def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    fig, axes = plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axis('off')
        if titles:
            ax.set_title(titles[i])
    plt.tight_layout()
    return axes

# iter() 把它变成迭代器
# next() 取出其中的第一批数据
X, y = next(iter(data.DataLoader(mnist_train, batch_size=18))) 
# 默认情况下X的形状是[18,1,28,28]，但是现在不需要通道1
show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y));

读取小批量

通过内置数据迭代器，可以随机打乱所有样本，并在每次迭代中读取一小批量数据，大小为batch_size

batch_size = 256

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

train_iter = data.DataLoader(
    mnist_train,          # 数据集
    batch_size,           # 每批样本数量
    shuffle=True,         # 打乱数据顺序(提高泛化性)
    num_workers=get_dataloader_workers()  # 并行加载线程数
)

利用之前定义的定时器类来计时

timer = Timer()
for X,y in train_iter:
    continue
print(f"{timer.stop():.2f} seconds") 
# 4.32 seconds

整合所有组件

定义load_data_fashion_mnist函数，用于获取和读取Fashion-MNIST数据集

这个函数返回训练集和验证集的数据迭代器

此外这个函数还接受一个可选参数resize，用来将图像大小调整为另一种形状

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize: # 如果传入了 resize 参数，先进行一个图像尺寸调整操作
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans) # 把多个图像变换组合成一个整体
    mnist_train = torchvision.datasets.FashionMNIST(
        root="data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="data", train=False, transform=trans, download=True)
    # 返回两个加载器
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
    print(X.shape, X.dtype, y.shape, y.dtype)
    break

torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64

如果减少batch_size(如减少到1)是否会影响读取性能？

当然，会让 I/O 频率变高、CPU 多进程效率下降、GPU 并行利用率变差

timer = Timer()
for bs in [1,16,64,256]:
    timer.start()
    train_iter = data.DataLoader(mnist_train, batch_size=bs, shuffle=True,num_workers=get_dataloader_workers())
    for X,y in train_iter:
        pass
    total_time = timer.stop()  # 得到这次的总时间
    print(f"batch size: {bs}, total time: {total_time:.2f}")

softmax回归的底层实现

使用刚刚引入的Fashion-MNIST数据集，并设置数据迭代器的批量大小为256

batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size)

初始化模型参数

现在暂时只把每个像素位置看作一个特征，原始数据集中的每个样本都是$28 \times 28$的图像，展平每个图像看作长度为784的向量

在softmax回归中，输出与类别一样多，所以网络输出维度为10

权重构建为$784 \times 10$的矩阵，偏置将构成一个$1 \times 10$的行向量，将使用正态分布初始化权重，偏置初始化为0

num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

定义softmax

当调用sum运算符时，可以指定保持在原始张量的轴数，而不折叠求和的维度

实现softmax由三个步骤组成：

1. 对每个项求幂(使用exp)
2. 对每一行求和(小批量中每个样本是一行)，得到每个样本的规范化常数
3. 将每一行除以其规范化常数，确保结果的和为1

def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

对于任何随机输入，将每个元素变成一个非负数，并且依据概率原理，每行总和为1

虽然这在数学上看起来是正确的，但在代码实现中有点草率，矩阵中的非常大或非常小的元素可能造成数值上溢或下溢

因为计算机中并不是用“数学上的实数”，而是用浮点数，可表示范围有限，如果x很大或者很小，分子分母都可能出现inf，导致出现NaN，这对于训练神经网络是灾难

如何解决这个问题呢？

对 softmax 的每一行向量减去它的最大值，不影响结果，却能避免溢出

def softmax(X):
    X_max = X.max(dim=1, keepdim=True).values
    X_exp = torch.exp(X - X_max)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition

$$
\operatorname{softmax}\left(x_{i}\right)=\frac{e^{x_{i}}}{\sum_{j} e^{x_{j}}}=\frac{e^{x_{i}-\max (x)}}{\sum_{j} e^{x_{j}-\max (x)}}
$$

数值上完全等价，但避免了 exp(大数) 的爆炸

定义模型

神经网络要求输入是二维的 (batch_size, feature_dim)

将数据传递到模型之前，使用reshape函数将每张原始图像展平为向量

定义输入如何通过网络映射到输出
$$
\color{purple} {\hat{\mathbf{y}}} = \mathbf{X} \mathbf{w} + b
$$

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)
# X从 (batch_size, 1, 28, 28) 被展平为 (batch_size, W.shape[0])
# 点乘后矩阵大小为(batch_size, 10)
# b被广播为(batch_size, 10)

定义损失函数

引入交叉熵损失函数，深度学习中最常见的损失函数，因为目前分类问题的数量远远超过回归问题的数量

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y]) # 批量索引y_hat[i, y[i]]

这里也会出现一个定义问题，假如y_hat(预测概率)非常接近 0，会因为浮点误差导致变成0，出现inf

可以给log加一个小常数避免数值溢出

def cross_entropy(y_hat, y):
    eps = 1e-8
    return -torch.log(y_hat[range(len(y_hat)), y] + eps)

这里用到多维索引，一次性指定所有维度的索引，不需要逐层访问

分类精度

给定预测概率分布y_hat，必须输出硬预测(hard prediction)时，通常选择预测概率最高的类，分类精度即正确预测数量与总预测数量之比

虽然直接优化精度可能很困难(因为精度的计算不可导)，但精度通常是最关心的性能衡量标准

如果y_hat是矩阵，那么假定第二个维度存储每个类的预测分数，使用argmax获得每行中最大元素的索引来获得预测类别，然后将预测类别与真实y元素进行比较

结果是一个包含0(错)和1(对)的张量，最后求和会得到正确预测的数量

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1: # 判断是否是多分类概率输出
        y_hat = y_hat.argmax(axis=1) # 取出预测概率最大的类别索引
    cmp = y_hat.type(y.dtype) == y   # == 保证数据类型一致
    return float(cmp.type(y.dtype).sum())  # 把bool转为数值求sum，转为float方便后续

y_hat = torch.tensor([[0.1, 0.9, 0.0], [0.8, 0.1, 0.1], [0.3, 0.3, 0.4]])
y = torch.tensor([1, 0, 2])
accuracy(y_hat, y)  # 输出3.0，因为都匹配上了

对于任意数据迭代器data_iter可访问的数据集，可以评估在任意模型net的精度

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n): # n表示多少个变量
        self.data = [0.0] * n

    def add(self, *args):  # *args 允许同时传入多个值，但个数必须等于n
        # zip(self.data, args) 会把当前累计值与新输入配对相加
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx): # 配置索引访问
        return self.data[idx]

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module): # 判断 net 是否是 PyTorch 模型
        net.eval()  # 将模型设置为评估模式，数值更稳定
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad(): # 禁用梯度计算
        for X, y in data_iter:
            # 累积预测正确数量与样本总数
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

优化算法

对于优化函数，使用之前定义的小批量随机梯度下降来优化模型的损失函数，设置学习率为0.1

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad(): # 以下操作不追踪梯度，优化步骤常用
        for param in params:
            # param.grad PyTorch 自动计算得到的梯度
            param -= lr * param.grad / batch_size
            param.grad.zero_()  # 清除梯度累积，结尾 _ 表示这是原地操作

训练

首先定义一个函数来训练一个迭代周期，updater是更新模型参数的常用函数，它接受批量大小作为参数

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回平均训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

定义一个在动画中绘制数据的类Animator

class Animator:
    """在动画中绘制数据"""
    def __init__(self, xlabel=None, ylabel=None, legend=None,
                 xlim=None, ylim=None,
                 xscale='linear', yscale='linear',
                 fmts=('-', 'm--', 'g-.', 'r:'),
                 nrows=1, ncols=1, figsize=(8, 6)):
        # 创建绘图窗口
        if legend is None:
            legend = []
        self.fig, self.axes = plt.subplots(nrows, ncols, figsize=figsize)

        # 若只有一个子图，统一处理为列表
        if nrows * ncols == 1:
            self.axes = [self.axes]
        self.X, self.Y, self.fmts = None, None, fmts

        # 坐标轴设置函数
        def set_axes():
            ax = self.axes[0]
            ax.set_xlabel(xlabel)
            ax.set_ylabel(ylabel)
            ax.set_xscale(xscale)
            ax.set_yscale(yscale)
            if xlim: ax.set_xlim(xlim)
            if ylim: ax.set_ylim(ylim)
            if legend: ax.legend(legend)
            ax.grid(True)
        self.config_axes = set_axes

    def add(self, x, y):
        """增量绘制多条曲线"""
        if not hasattr(y, "__len__"):
            y = [y]
        n = len(y)
        if not hasattr(x, "__len__"):
            x = [x] * n
        # 初始化 X, Y 容器
        if not self.X:
            self.X = [[] for _ in range(n)]
        if not self.Y:
            self.Y = [[] for _ in range(n)]
        # 添加数据点
        for i, (a, b) in enumerate(zip(x, y)):
            if a is not None and b is not None:
                self.X[i].append(a)
                self.Y[i].append(b)

    def show(self):
        """训练结束后绘制最终曲线"""
        self.axes[0].cla()
        for x, y, fmt in zip(self.X, self.Y, self.fmts):
            self.axes[0].plot(x, y, fmt)
        self.config_axes()
        plt.show()

实现一个训练函数，它会在train_iter访问到的训练数据集上训练一个模型net

该训练函数将会运行多个迭代周期，在每个迭代周期结束时，利用test_iter访问到的测试数据集对模型进行评估，最后利用Animator类来可视化训练过程

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        train_loss, train_acc = train_metrics
        print(f"Epoch {epoch+1:>2d}/{num_epochs}: "
              f"loss={train_loss:.4f}, train_acc={train_acc:.3f}, test_acc={test_acc:.3f}")
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    print(f"Final loss {train_loss:.3f}, train acc {train_acc:.3f}, test acc {test_acc:.3f}")
    animator.show()  # 在最后绘图

启动代码部分

batch_size = 256
lr = 0.1
train_iter, test_iter = load_data_fashion_mnist(batch_size)
num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

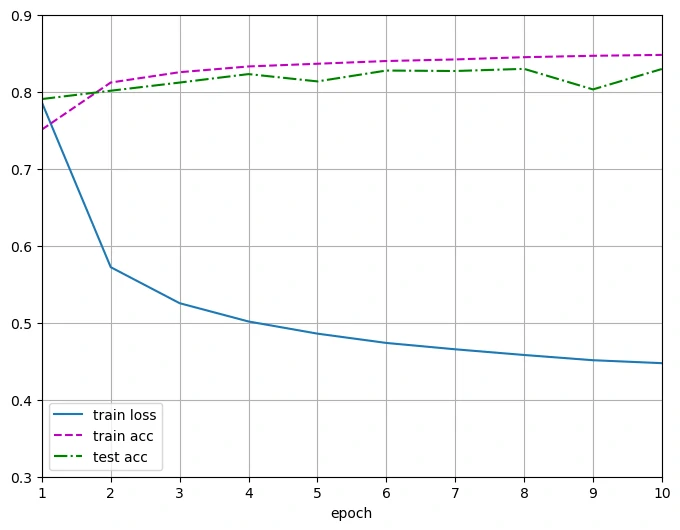
输出结果

Final loss 0.448, train acc 0.847, test acc 0.830

预测

现在训练已经完成，模型已经准备好对图像进行分类预测

给定一系列图像将比较它们的实际标签(文本输出的第一行)和模型预测(文本输出的第二行)

def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签"""
    for X, y in test_iter:
        break
    trues = get_fashion_mnist_labels(y)
    preds = get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)  # 刚刚已经训练好模型的w和b了，直接调用即可

训练softmax回归循环模型与训练线性回归模型非常相似：先读取数据，再定义模型和损失函数，然后使用优化算法训练模型，大多数常见的深度学习模型都有类似的训练过程

练习题

1. 返回概率最大的分类标签总是最优解吗？例如，医疗诊断场景下可以这样做吗？

   softmax 只考虑“哪个更可能”，却不知道“这个决策带来的后果”，所以这些领域往往要引入阈值决策(decision threshold)，而不是简单地取 argmax

2. 假设使用softmax回归来预测下一个单词，可选取的单词数目过多可能会带来哪些问题?

   问题类别	产生原因	后果	解决方法
   计算量爆炸	词表太大，每次都要算所有词的 exp	训练极慢	Hierarchical Softmax, Sampled Softmax
   数值不稳定	exp(大数) 溢出, exp(小数) 下溢	NaN、梯度消失	减最大值、Log-Softmax
   内存消耗高	最后一层参数量随词表线性增长	显存不足	参数分片、低秩分解、稀疏更新
   模型不平衡	高频词梯度主导	泛化差	采样修正、词频平衡

softmax回归的简洁实现

通过深度学习框架的高级API也能更方便地实现softmax回归模型，继续使用Fashion-MNIST数据集，并保持批量大小为256

batch_size = 256
train_iter, test_iter = load_data_fashion_mnist(batch_size)

初始化模型参数

softmax回归的输出层是一个全连接层，为了实现模型，只需在Sequential中添加一个带有10个输出的全连接层，仍然以均值0和标准差0.01随机初始化权重

# PyTorch不会隐式地调整输入的形状
# 因此在线性层前定义了展平层(flatten)，来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights)

softmax的实现

在底层实现时考虑到可以从所有$o_k$中减去$\max(o_k)$避免上溢，这是可行的，但是可能$o_j - \max(o_k)$具有较大的负值，$\exp(o_j - \max(o_k))$可能会出现下溢的情况，使得$\log(\hat y_j)$为-inf

通过将softmax和交叉熵结合在一起，可以避免反向传播过程中可能会困扰的数值稳定性问题
$$
\begin{split}\begin{aligned}
\log{(\hat y_j)} & = \log\left( \frac{\exp(o_j - \max(o_k))}{\sum_k \exp(o_k - \max(o_k))}\right) \\
& = \log{(\exp(o_j - \max(o_k)))}-\log{\left( \sum_k \exp(o_k - \max(o_k)) \right)} \\
& = o_j - \max(o_k) -\log{\left( \sum_k \exp(o_k - \max(o_k)) \right)}.
\end{aligned}\end{split}
$$
这样就没有将softmax概率传递到损失函数中，而是在交叉熵损失函数中传递未规范化的预测，在同一过程中同时得到 softmax 和它的对数，以避免数值溢出并提高计算效率

loss = nn.CrossEntropyLoss(reduction='none')

优化算法

使用学习率为0.1的小批量随机梯度下降作为优化算法

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

训练

训练函数仍用之前定义的

num_epochs = 10
train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

和以前一样，这个算法使结果收敛到一个相当高的精度，而且这次的代码比之前更精简了

Final loss 0.448, train acc 0.849, test acc 0.811

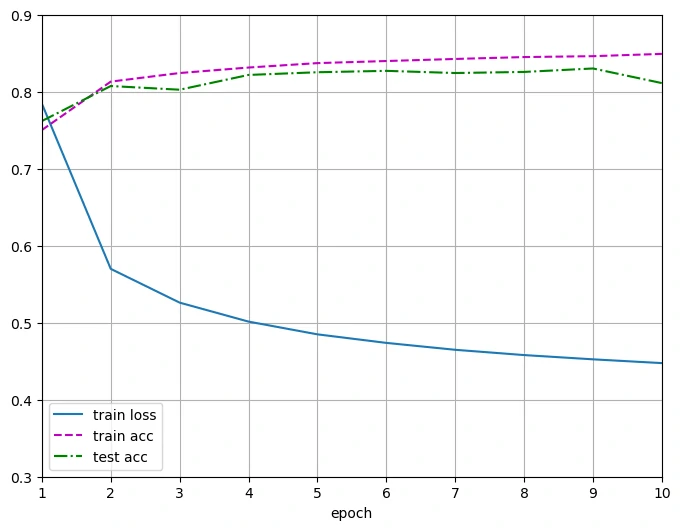
在图上会发现一个现象，第10轮的精度比第9轮的下降了，意味着模型已经开始拟合噪声，而非通用特征，也就是常说的过拟合(overfitting)

在这个例子中Fashion-MNIST并不是很复杂，使用的模型参数却有784个，网络太过复杂化，就容易陷入过拟合

过拟合的解决在多层感知机部分讲解