神经网络研究人员已经从考虑单个人工神经元的行为转变为从层的角度构思网络，通常在设计架构时考虑的是更粗糙的块(block)

将深入探索深度学习计算的关键组件，即模型构建、参数访问与初始化、设计自定义层和块、将模型读写到磁盘，以及利用GPU实现显著的加速

层和块

单个输出的线性神经网络模型：接收输入、生成标量输出，并通过可调参数优化目标函数

扩展到多输出网络时，可用矢量化算法统一描述整层神经元的行为

层与单个神经元类似，Softmax 回归中单层即可构成模型，而多层感知机在此基础上通过层的堆叠保留了相同的基本结构

在多层感知机中，整个模型及各层都遵循这种架构：模型接收特征并生成预测，各层接收上一层输出并传递结果，同时通过反向传播更新参数

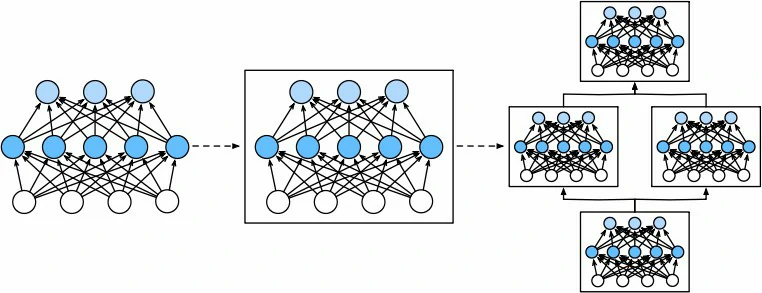
研究常聚焦于介于“单层”和“整体模型”之间的结构，例如ResNet-152由层组(groups of layers)重复堆叠而成，赢得了2015年ImageNet和COCO计算机视觉比赛的识别和检测任务，并成为视觉任务的主流架构，类似的分层设计在 NLP 和语音领域也已普遍采用

为构建这类复杂网络，引入了神经网络**块(block)**的概念，块可表示单个层、由多个层组成的组件或整个模型本身

利用块进行递归式组合，可通过简洁的代码实现结构灵活、复杂度可控的神经网络

blocks

从编程的角度来看，块由**类(class)**表示

之前一直在通过net(X)调用模型来获得模型的输出，实际上是net.__call__(X)的简写

这个前向传播函数非常简单：它将列表中的每个块连接在一起，将每个块的输出作为下一个块的输入

自定义块

每个块必须提供的基本功能：

  1. 将输入数据作为其前向传播函数的参数
  2. 通过前向传播函数来生成输出，输出形状和输入形状无关
  3. 计算其输出关于输入的梯度，可通过其反向传播函数进行访问，通常这是自动发生的
  4. 存储和访问前向传播计算所需的参数
  5. 根据需要初始化模型参数

实现一个块类，包含一个多层感知机，其具有256个隐藏单元的隐藏层和一个10维输出层

MLP类继承了表示块的类，只需要提供自己的构造函数(Python中的__init__函数)和前向传播函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from torch import nn
from torch.nn import functional as F
class MLP(nn.Module):
    def __init__(self):
        # 调用MLP的父类Module的构造函数来执行必要的初始化
        # 在类实例化时也可以指定其他函数参数，例如模型参数params(稍后将介绍)
        super().__init__()  # 显式调用父类的构造函数，固定写法
        self.hidden = nn.Linear(20, 256)  # 隐藏层
        self.out = nn.Linear(256, 10)  # 输出层

    # 定义模型的前向传播，即如何根据输入X返回所需的模型输出
    def forward(self, X):
        # 注意，这里使用ReLU的函数版本，其在nn.functional模块中定义
        return self.out(F.relu(self.hidden(X)))

来试一下这个函数

1
2
X = torch.rand(2, 20)
net = MLP()

块的一个主要优点是它的多功能性，可以子类化块以创建层(如全连接层的类)、整个模型(如上面的MLP类)或具有中等复杂度的各种组件

顺序块

为了构建自己的简化的MySequential，只需要定义两个关键函数：

  1. 一种将块逐个追加到列表中的函数
  2. 一种前向传播函数，用于将输入按追加块的顺序传递给块组成的“链条”

下面的MySequential类提供了与默认Sequential类相同的功能

1
2
3
4
5
6
7
8
9
class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        self.blocks = nn.ModuleList(args)  # 以列表形式自动注册块，不用循环
        
    def forward(self, X):
        for block in self.blocks: # 循环块进行网络传播
            X = block(X)
        return X

__init__函数将每个模块逐个添加到有序字典_modules中

现在可以使用MySequential类重新实现多层感知机

1
net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))

前向传播函数

Sequential类使模型构造变得简单，允许组合新的架构，而不必定义自己的类

有时希望合并既不是上一层的结果也不是可更新参数的项，称之为常数参数(constant parameter)

需要一个计算函数$f(\mathbf{x},\mathbf{w}) = c \cdot \mathbf{w}^\top \mathbf{x}$的层，其中$\mathbf{x}$是输入，$\mathbf{w}$是参数，$c$是某个在优化过程中没有更新的指定常量

实现了一个FixedHiddenMLP类，如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        # requires_grad设置False，参数在训练过程中保持固定不变
        self.rand_weight = torch.rand((20, 20), requires_grad=False) #
        self.linear = nn.Linear(20, 20)

    def forward(self, X):
        X = self.linear(X)
        # 使用创建的常量参数以及relu和mm函数
        X = F.relu(torch.mm(X, self.rand_weight) + 1) #引入非线性和固定随机特征映射
        X = self.linear(X) # 参数共享的第二次线性变换
        # 控制流
        while X.abs().sum() > 1:
            X /= 2
        return X.sum()

实现了一个隐藏层，其权重(self.rand_weight)在实例化时被随机初始化，之后为常量

直接调用类就可以实现网络构建

1
net = FixedHiddenMLP()

可以混合搭配各种组合块的方法实现嵌套

1
2
3
4
5
6
7
8
9
class NestMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),
                                 nn.Linear(64, 32), nn.ReLU())
        self.linear = nn.Linear(32, 16)

    def forward(self, X):
        return self.linear(self.net(X))
1
chimera = nn.Sequential(NestMLP(), nn.Linear(16, 20), FixedHiddenMLP())

思考题

  1. 如果将MySequential中存储块的方式更改为Python列表，会出现什么样的问题？

    把层存在 Python 列表里，PyTorch 就完全看不到它们

    不会报错，但是参数不会更新、设备不会同步、模型不会保存

  2. 实现一个块，它以两个块为参数，例如net1和net2，并返回前向传播中两个网络的串联输出，这也被称为平行块

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    class ParallelBlock(nn.Module):
        def __init__(self, net1, net2):
            super().__init__()
            self.net1 = net1
            self.net2 = net2
        
        def forward(self, X):
            # 分别通过两个网络
            Y1 = self.net1(X)
            Y2 = self.net2(X)
            # 特征上拼接
            return torch.cat((Y1, Y2), dim=1)

    如果要实现多个网络的拼接，利用ModuleList()

    1
    2
    3
    4
    5
    6
    7
    8
    class MultiParallelBlock(nn.Module):
        def __init__(self, *nets):
            super().__init__()
            self.nets = nn.ModuleList(nets)  # 自动注册所有子模块

        def forward(self, X):
            outputs = [net(X) for net in self.nets] # 依次传播X
            return torch.cat(outputs, dim=1) # 列方向拼接输出

参数管理

在选择了架构并设置了超参数后进入训练阶段，目标是找到使损失函数最小化的模型参数值

有时希望提取参数，或者说将模型保存下来，以便它可以在其他软件中执行

先定义一个具有单隐藏层的多层感知机

1
2
3
4
5
6
import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)

参数访问

当通过Sequential类定义模型时，可以通过索引来访问模型的任意层，每层的参数都在其属性中

1
print(net[2].state_dict())
1
OrderedDict([('weight', tensor([[ 0.0763, -0.1380,  0.0337,  0.3220,  0.3303,  0.2827,  0.0141,  0.3154]])), ('bias', tensor([-0.2091]))])

在nn.Sequential中$y=Xw^T+b$，所以shape是torch.Size([1, 8])

目标参数

每个参数都表示为参数类的一个实例，要对参数执行任何操作，首先需要访问底层的数值

1
2
3
print(net[2].weight)
print(net[2].bias)
print(net[2].bias.data) 
1
2
3
4
5
6
Parameter containing:
tensor([[ 0.0763, -0.1380,  0.0337,  0.3220,  0.3303,  0.2827,  0.0141,  0.3154]],
       requires_grad=True)
Parameter containing:
tensor([-0.2091], requires_grad=True)
tensor([-0.2091])

参数是复合的对象，包含值、梯度和额外信息

刚刚还没调用方向传播，所以参数的梯度处于初始状态

1
net[2].weight.grad == None  # True

遍历参数

需要对所有参数执行操作时，逐个访问它们可能会很麻烦，如果是复杂块(比如嵌套)，需要递归来实现

对比访问方式：

1
2
3
4
# 单层
print(*[(name, param.shape) for name, param in net[0].named_parameters()])
# 全部
print(*[(name, param.shape) for name, param in net.named_parameters()])

*用于解包，让打印结果更干净、无方括号

1
2
('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))

可以发现每一层的命名方法，因此可以利用刚刚的字典结构去访问具体参数

1
print(net.state_dict()['0.weight'])

从嵌套块收集参数

如果将多个块相互嵌套，参数命名约定是如何工作的？

首先定义一个生成块的函数，然后将这些块组合到更大的块中

1
2
3
4
5
6
7
8
9
10
def block1():
    return nn.Sequential(nn.Linear(4,8), nn.ReLU(),
                         nn.Linear(8,4), nn.ReLU())
def block2():
    net = nn.Sequential()
    for i in range(4):
        net.add_module(f"block{i}", block1())
    return net

rgnet = nn.Sequential(block2(),nn.Linear(4,1))

设计了网络后，看看它是如何工作的

1
print(rgnet)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Sequential(
  (0): Sequential(
    (block0): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block1): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True) # 一会访问的位置
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block2): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
    (block3): Sequential(
      (0): Linear(in_features=4, out_features=8, bias=True)
      (1): ReLU()
      (2): Linear(in_features=8, out_features=4, bias=True)
      (3): ReLU()
    )
  )
  (1): Linear(in_features=4, out_features=1, bias=True)
)

因为层是分层嵌套的，所以也可以像通过嵌套列表索引一样访问它们

访问第一个主要的块中、第二个子块的第一层的偏置项

1
rgnet[0][1][0].bias

参数初始化

深度学习框架提供默认随机初始化，也允许创建自定义初始化方法，满足通过其他规则实现初始化权重

默认情况下，PyTorch会根据一个范围均匀地初始化权重和偏置矩阵，这个范围是根据输入和输出维度计算出的

内置初始化

这里的tensor常为weightorbias

常规初始化

1
2
3
4
5
nn.init.constant_(tensor, val)       # 所有元素设为常数
nn.init.zeros_(tensor)               # 全零
nn.init.ones_(tensor)                # 全一
nn.init.uniform_(tensor, a, b)       # 均匀分布 U(a, b)
nn.init.normal_(tensor, mean, std)   # 正态分布 N(mean, std)

Xavier(Glorot)初始化

保持前后层的方差一致，防止梯度消失或爆炸，常用于 Sigmoid 或 tanh 激活

1
2
nn.init.xavier_uniform_(tensor)
nn.init.xavier_normal_(tensor)

Kaiming(He)初始化

适用于 ReLU 或 LeakyReLU 激活函数

1
2
nn.init.kaiming_uniform_(tensor, nonlinearity='relu')
nn.init.kaiming_normal_(tensor, nonlinearity='relu')

正交初始化

保持权重矩阵的正交性，广泛用于循环神经网络(RNN/LSTM)，可以避免梯度爆炸

1
nn.init.orthogonal_(tensor)

稀疏初始化

让部分连接为0，适合稀疏神经网络

1
nn.init.sparse_(tensor, sparsity=0.1)

自定义初始化

有时，深度学习框架没有提供需要的初始化方法
$$
\begin{split}\begin{aligned}
w \sim \begin{cases}
U(5, 10) & p= \frac{1}{4} \\
0 & p= \frac{1}{2} \\
U(-10, -5) & p= \frac{1}{4}
\end{cases}
\end{aligned}\end{split}
$$
实现了一个my_init函数来应用到net

1
2
3
4
5
6
7
def my_init(m):
    if(type(m)==nn.Linear):
        print("Init", *[(name,param.shape) for name, param in m.named_parameters()][0])
        nn.init.uniform_(m.weight, -10,10)
        m.weight.data *= m.weight.data.abs()>=5
        
net.apply(my_init)
1
2
3
4
5
6
7
Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])
Sequential(
  (0): Linear(in_features=4, out_features=8, bias=True)
  (1): ReLU()
  (2): Linear(in_features=8, out_features=1, bias=True)
)

参数绑定

有时希望在多个层间共享参数：可以定义一个稠密层，然后使用它的参数来设置另一个层的参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
shared = nn.Linear(8,8)
net = nn.Sequential(nn.Linear(4,8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.Linear(8,1))
# 前向传播(只是为了初始化参数)
net(X)
# 检查共享层权重是否相同
print(torch.equal(net[2].weight[0], net[4].weight[0]))
# 修改参数(安全方式，不用 .data)
with torch.no_grad():
    net[2].weight[0,0]=100
# 检查是否一起变化
print(torch.equal(net[2].weight[0], net[4].weight[0]))
# 验证：它们指向同一块内存
print(net[2].weight.data_ptr() == net[4].weight.data_ptr())

不用 .data，改用 with torch.no_grad()，这让修改参数不会被 autograd 追踪，也不会破坏计算图

当参数绑定时，梯度会发生什么情况？

由于模型参数包含梯度，因此在反向传播期间第二个隐藏层(即第三个神经网络层)和第三个隐藏层(即第五个神经网络层)的梯度会加在一起

延后初始化

在之前的定义中可能会有一些疑问：

  1. 定义了网络架构，但没有指定输入维度
  2. 添加层时没有指定前一层的输出维度
  3. 在初始化参数时，甚至没有足够的信息来确定模型应该包含多少参数

这里用到了框架的延后初始化(defers initialization)，即直到数据第一次通过模型传递时，框架才会动态地推断出每个层的大小

当使用卷积神经网络时，由于输入维度(即图像的分辨率)将影响每个后续层的维数，在编写代码时无须知道维度是什么就可以设置参数，这种能力可以大大简化定义和修改模型的任务

实例化网络

实例化一个多层感知机

1
2
3
4
5
import tensorflow as tf
net = tf.keras.models.Sequential([
    tf.keras.layers.Dense(256, activation=tf.nn.relu),
    tf.keras.layers.Dense(10),
])

这里用到了tensorflow，相比torch.nn不需要再显式指定输入维度

概念 PyTorch 写法 TensorFlow 写法
定义模型 nn.Sequential([...]) tf.keras.models.Sequential([...])
层的基类 nn.Module tf.keras.layers.Layer
全连接层 nn.Linear(in, out) tf.keras.layers.Dense(out)
激活函数 nn.ReLU() activation=tf.nn.relu
模型调用 net(x) net(x)

为输入维数是未知的，所以网络不可能知道输入层权重的维数

框架尚未初始化任何参数，通过尝试访问以下参数进行确认

1
[net.layers[i].get_weights() for i in range(len(net.layers))] 
1
[[], []]

每个层对象都存在，但权重为空

使用net.get_weights()将抛出一个错误，因为权重尚未初始化

让将数据通过网络，最终使框架初始化参数

1
2
3
X = tf.random.uniform((2, 20))
net(X)
[w.shape for w in net.get_weights()]
1
[(20, 256), (256,), (256, 10), (10,)]

当知道输入维度为20时，框架可以通过代入值20来识别第一层权重矩阵的形状，识别出第一层的形状后，框架处理第二层，依此类推，直到所有形状都已知为止

在这种情况下，只有第一层需要延迟初始化，但是框架仍是按顺序初始化的，等到知道了所有的参数形状，框架就可以初始化参数

思考题

  1. 如果指定了第一层的输入尺寸，但没有指定后续层的尺寸，会发生什么？是否立即进行初始化？

    指定第一层的输入形状，只会让第一层立即建权重；后续层仍然是延迟初始化，直到真正看到数据流动时才构建

    1
    2
    3
    4
    5
    net = tf.keras.models.Sequential([
        tf.keras.layers.Dense(256, activation=tf.nn.relu, input_shape=(4,)),
        tf.keras.layers.Dense(128),
        tf.keras.layers.Dense(10)
    ])

  2. 如果指定了不匹配的维度会发生什么？

    会在第一次真正使用模型时检查输入输出维度是否一致，一旦不匹配，就立即抛出ValueError

  3. 如果输入具有不同的维度，需要做什么？

    场景 例子 解决思路
    每个样本特征数不同 文本句长不一、时间序列长短不一 padding、截断
    多模态输入 图像+文本、图像+数值 使用Functional API
    定义多个 Input

自定义层

不带参数的层

下面的CenteredLayer类要从其输入中减去均值，没有任何参数

要构建它，只需继承基础层类并实现前向传播功能

1
2
3
4
5
6
class CenteredLayer(nn.Module):
    def __init__(self):
        super().__init__()
    
    def forward(self, X):
        return X - X.mean()

向该层提供一些数据，验证它是否能按预期工作

1
2
layer = CenteredLayer()
layer(torch.FloatTensor([1, 2, 3, 4, 5]))
1
tensor([-2., -1.,  0.,  1.,  2.])

确实可行，可以将层作为组件合并到更复杂的模型中

1
2
3
net = nn.Sequential(nn.Linear(8,128), CenteredLayer())
Y = net(torch.rand(4,8))
Y.mean() # 输出0

因为减去自身均值后，全局平均一定为 0

带参数的层

定义具有参数的层，这些参数可以通过训练进行调整

可以使用内置函数来创建参数，这些函数提供一些基本的管理功能，比如管理访问、初始化、共享、保存和加载模型参数

实现自定义版本的全连接层，该层需要两个参数，一个表示权重，一个表示偏置

需要输入参数：in_units和out_units，分别表示输入数和输出数

1
2
3
4
5
6
7
8
9
10
11
class MyLinear(nn.Module):
    def __init__(self, in_units, out_units):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(in_units, out_units))
        self.bias = nn.Parameter(torch.randn(out_units,))
    def forward(self, X):
        linear = torch.matmul(X, self.weight) + self.bias
        return F.relu(linear)

linear = MyLinear(5,3)
linear.weight
1
2
3
4
5
6
Parameter containing:
tensor([[ 0.3906,  1.1024,  0.6969],
        [ 0.4338, -1.2284,  0.7065],
        [ 0.5477, -0.0035,  1.0133],
        [-0.6144,  1.4496, -0.5322],
        [-1.2321,  0.1517, -1.1284]], requires_grad=True)

可以使用自定义层直接执行前向传播计算

1
print(linear(torch.rand(2, 5)))
1
2
tensor([[1.2887, 2.0474, 0.4946],
        [0.6648, 1.4507, 0.0000]], grad_fn=<ReluBackward0>)

读写文件

保存训练的模型，以备将来在各种环境中使用(比如在部署中进行预测)

当运行一个耗时较长的训练过程时，最佳的做法是定期保存中间结果，以确保在服务器电源被不小心断掉时，不会损失几天的计算结果

加载和保存张量

保存方式
单个张量 torch.save(x, 'x-file')
张量列表 torch.save([x, y],'x-files')
张量字典 torch.save(mydict, 'mydict')

读回方式基本相同，不同的是接受容器要准备好

1
2
3
x2 = torch.load('x-file', weights_only=True)      # 单个张量
x2, y2 = torch.load('x-files', weights_only=True) # 张量列表
mydict2 = torch.load('mydict', weights_only=True) # 字典

加载和保存模型参数

保存单个权重向量(或其他张量)确实有用，但是如果想保存整个模型，并在以后加载它们，单独保存每个向量则会变得很麻烦

深度学习框架提供了内置函数来保存和加载整个网络，这将保存模型的参数而不是保存整个模型

因为模型本身可以包含任意代码，所以模型本身难以序列化

为了恢复模型，需要用代码生成架构，然后从磁盘加载参数

1
2
3
4
5
6
7
8
9
10
11
12
class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(20, 256)
        self.output = nn.Linear(256, 10)

    def forward(self, x):
        return self.output(F.relu(self.hidden(x)))

net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)

将模型的参数存储在一个叫做“mlp.params”的文件中

1
torch.save(net.state_dict(), 'mlp.params')

为了恢复模型，实例化了原始多层感知机模型的一个备份，这里不需要随机初始化模型参数，而是直接读取文件中存储的参数

1
2
3
clone = MLP()
clone.load_state_dict(torch.load('mlp.params',weights_only=True))
clone.eval()
1
2
3
4
MLP(
  (hidden): Linear(in_features=20, out_features=256, bias=True)
  (output): Linear(in_features=256, out_features=10, bias=True)
)

在输入相同的X时，两个实例的计算结果应该相同

1
2
Y_clone = clone(X)
torch.equal(Y_clone, Y) # True

GPU

使用nvidia-smi命令来查看显卡信息

1
nvidia-smi

计算设备

在PyTorch中，CPU和GPU可以用torch.device('cpu') 和torch.device('cuda')表示

如果有多个GPU，使用torch.device(f'cuda:{i}') 来表示第$i$块GPU(从0开始)

查询可用gpu的数量

1
torch.cuda.device_count()

定义了两个方便的函数，这两个函数允许在不存在所需所有GPU的情况下运行代码

1
2
3
4
5
6
7
8
9
10
11
12
13
def try_gpu(i=0):  #@save
    """如果存在，则返回gpu(i)，否则返回cpu()"""
    if torch.cuda.device_count() >= i + 1:
        return torch.device(f'cuda:{i}')
    return torch.device('cpu')

def try_all_gpus():  #@save
    """返回所有可用的GPU，如果没有GPU，则返回[cpu(),]"""
    devices = [torch.device(f'cuda:{i}')
             for i in range(torch.cuda.device_count())]
    return devices if devices else [torch.device('cpu')]

try_gpu(), try_all_gpus()
1
(device(type='cuda', index=0), [device(type='cuda', index=0)])

张量与GPU

默认情况下，张量是在CPU上创建的

1
2
x = torch.tensor([1, 2, 3])
x.device
1
device(type='cpu')

无论何时要对多个项进行操作，它们都必须在同一个设备上，否则框架将不知道在哪里存储结果，甚至不知道在哪里执行计算

存储在GPU上

可以在创建张量时指定存储设备，在GPU上创建的张量只消耗这个GPU的显存

1
2
X = torch.ones(2, 3, device=try_gpu())
X
1
2
tensor([[1., 1., 1.],
        [1., 1., 1.]], device='cuda:0')

复制

如果创建了两个量在不同设备上，不能直接将它们相加，在同一设备上找不到数据会导致失败

copyto

假设变量X已经存在于第一个GPU上，调用X.cuda(0)将返回X而不会复制并分配新内存

1
X.cuda(0) is X  # True

旁注

GPU的计算速度很快，但设备间的数据传输(如 CPU 与 GPU 之间)要慢得多

为了减少等待和阻塞，应尽量减少拷贝操作，将多个小操作合并成较大的批量计算，频繁的数据交换会拖慢并行效率

当打印张量或转换为NumPy时，若数据不在内存中，系统会先将其拷回CPU，这也会增加传输开销，并受Python全局解释器锁的影响

GPU快在计算，慢在传输，减少数据移动才能提高效率

神经网络与GPU

神经网络模型可以指定设备

1
2
net = nn.Sequential(nn.Linear(3, 1))
net = net.to(device=try_gpu())

当输入为GPU上的张量时，模型将在同一GPU上计算结果

1
net(X)
1
2
tensor([[0.5950],
        [0.5950]], device='cuda:0', grad_fn=<AddmmBackward0>)

确认模型参数存储在同一个GPU上

1
net[0].weight.device
1
device(type='cuda', index=0)

练习

尝试一个计算量更大的任务，比如大矩阵的乘法，看看CPU和GPU之间的速度差异，再试一个计算量很小的任务呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
timer = Timer()

# 定义大矩阵和小矩阵
sizes = {'大矩阵': 4096, '小矩阵': 32}

for name, n in sizes.items():
    print(f"\n{name}({n}x{n}):")

    A = torch.randn(n, n)
    B = torch.randn(n, n)

    # ---- CPU 计算 ----
    timer.start()
    C = A @ B
    cpu_time = timer.stop()

    # ---- GPU 计算(如果可用)----
    device = try_gpu()  # 自动选择可用 GPU 或 CPU
    if device.type == 'cuda':
        # 把数据搬到 GPU
        A_gpu, B_gpu = A.to(device), B.to(device)
        torch.cuda.synchronize()

        timer.start()
        C_gpu = A_gpu @ B_gpu
        torch.cuda.synchronize()
        gpu_time = timer.stop()

        print(f"CPU: {cpu_time * 1000:.3f} ms\tGPU: {gpu_time * 1000:.3f} ms\t加速比: {cpu_time / gpu_time:.1f}x")
    else:
        print(f"CPU: {cpu_time * 1000:.3f} ms\t(未检测到 GPU)")

1
2
3
4
5
大矩阵(4096x4096):
CPU: 616.677 ms	GPU: 195.000 ms	加速比: 3.2x

小矩阵(32x32):
CPU: 24.073 ms	GPU: 0.946 ms	加速比: 25.4x