COMSOL光电器件仿真
COMSOL内置物理参数
| 描述 | 名称 | 值 |
|---|---|---|
| 重力加速度 | g_const | 9.80665[m/s^2] |
| 阿伏加德罗常数 | N_A_const | 6.02214076e23[1/mol] |
| 玻尔兹曼常数 | k_B_const | 1.380649e-23[J/K] |
| 真空特性阻抗 (自由空间阻抗) |
Z0_const | 376.73031346177066[ohm] |
| 电子质量 | me_const | 9.10938291e-31[kg] |
| 元电荷 | e_const | 1.602176634e-19[C] |
| 法拉第常数 | F_const | 96485.3365[C/mol] |
| 精细结构常数 | alpha_const | 7.29735298e-3 |
| 万有引力常数 | G_const | 6.67384e-11[m^3/(kg*s^2)] |
| 理想气体摩尔体积 (273.15K,1atm) |
V_m_const | 2.2413968e-2[m^3/mol] |
| 中子质量 | mn_const | 1.674927351e-27[kg] |
| 真空磁导率(磁常数) | mu0_const | 2*alpha_const*h_const/c_const/e_const/e_const |
| 真空介电常数 | epsilon0_const | 1/mu0_const/c_const/c_const |
| 普朗克常数 | h_const | 6.62607015e-34[J*s] |
| 普朗克常数除以2pi | hbar_const | 1.05457172533629e-34[J*s] |
| 质子质量 | mp_const | 1.672621777e-27[kg] |
| 真空中的光速 | c_const | 299792458[m/s] |
| 玻尔兹曼常数 | sigma_const | 5.670373e-8[W/(m^2*K^4)] |
| 通用气体常数 | R_const | 8.3144621[J/(mol*K)] |
| 维恩位移定律常数 | b_const | 2.8977721e-3[m*K] |
一维PN结
理论基础
阳极接触与p型区相邻,阴极与n型区连接,基于麦克斯韦方程和玻耳兹曼方程推导出载流子输运的半导体模型(基于稳态问题):
半导体中的高斯定理(泊松方程)
描述电场与电荷密度的关系
$$
\begin{aligned} \nabla \cdot(\varepsilon \nabla V)=-q\left(p-n+N_{D}^{+}-N_{A}^{-}\right) \end{aligned}
$$
左边是电位移矢量($D=\varepsilon E = -\varepsilon \nabla V$)的散度,反映电场的通量(电荷),欠个负号
右边是负的电荷密度,$\rho = q\left(p-n+N_{D}^{+}-N_{A}^{-}\right)$是半导体中的总(+)电荷密度
在半导体的耗尽区,无自由载流子,但有电离的施主和受主,方程简化为:
$$
\begin{aligned}\nabla \cdot(\varepsilon \nabla V) = -q(N_D^{+} - N_A^{-}) \end{aligned}
$$
这与耗尽区的电荷分布一致(耗尽区的电荷由电离杂质决定)
电流连续性方程
描述载流子电流密度与SRH净复合率的关系($\nabla\cdot \vec J = -\partial \rho /\partial t$),是电荷守恒定律的体现
正值表示净流出,负值表示净流入,所以右侧负号
$$
\begin{aligned}
\nabla \cdot \vec J_n=-q R_{SRH} \qquad
\nabla \cdot \vec J_p=q R_{SRH}
\end{aligned}
$$
左边是载流子电流密度的散度,反映载流子数量的变化
当$R_{SRH}>0$(净复合)时,电子在某处减少(被复合),所以必须有电子电流汇入以补充,电流密度散度为负;对空穴来说,复合意味着空穴也减少,但由于空穴带正电,所以符号方向相反
在该案例中假设$R_{SRH}$是电子和空穴复合的唯一来源
$R_{SRH}$是
Shockley-Read-Hall复合速率,是硅基半导体的主要复合机制$R_{SRH} $理论详细见复合理论
假设等温、非简并半导体具有恒定的能带结构,电子流和空穴流表示为
$$
\begin{aligned}
\vec J_n =-n q \mu_{n} \nabla V+\mu_n k_B T \nabla n \qquad
\vec J_p =-p q \mu_{p} \nabla V-\mu_p k_B T \nabla p
\end{aligned}
$$
第一项为漂移电流,这部分由电场$E=-\nabla V$引起
$$
\begin{aligned}
\vec J_{n,drift}=qn\mu_nE \qquad
\vec J_{p,drift}=qp\mu_pE
\end{aligned}
$$
第二项为扩散电流,来源于浓度梯度
$$
\begin{aligned}\vec J_{n, diff}=\mu_n k_B T \nabla n \qquad \vec J_{p, diff}=-\mu_p k_B T \nabla p \end{aligned}
$$
可以用爱因斯坦关系式写的更熟悉些
$$
\begin{aligned} D_n =\mu_n \frac{k_B T}{q}\qquad D_p=\mu_p \frac{k_B T}{q} \end{aligned}
$$
得到
$$
\begin{aligned}\vec J_{n, diff}=q D_n \nabla n \qquad \vec J_{p, diff}=-q D_p \nabla p \end{aligned}
$$
负号来自于电流方向与$\nabla p$方向相反
模型定义
本例模型模拟p-n结在反向、平衡和正向偏压下的特性,模拟的结长度为$5\mu m$,p型掺杂侧和n型掺杂侧的净掺杂浓度均为$1\times 10^{15}cm^{-3}$
模型中还添加了Shockley-Read-Hall复合特征,用于模拟通常在间接带隙半导体(例如硅,本例模型中使用的材料)中发生的复合
模型采用文献中使用的材料参数,并比较不同偏压条件下(-4V、0V和0.5V)计算出的载流子浓度分布与参考文献中的相应结果
Kramer K M, Hitchon W N. Semiconductor devices: A simulation approach with CDROM[M]. Prentice Hall PTR, 1997.
使用两种不同的离散化方法来求解模型:有限元(FEM)对数形式离散法和有限体积(FVM)离散法
参数设置
全局定义
| 名称 | 表达式 | 描述 |
|---|---|---|
| Va | bias*sweep |
外加电压 |
| Tl | 300[K] | 晶格温度 |
| Na | 1e15[1/cm^3] | 受主浓度 |
| Nd | 1e15[1/cm^3] | 施主浓度 |
| epsilonr_param | 11.8 | 相对介电常数 |
| Eg0_param | 1.12[V] | 带隙 |
| chi0_param | 4.05[V] | 电子亲和能 |
| Ni | 1.25e10[1/cm^3] | 本征载流子浓度 |
| Nc_param | Ni*exp(Eg0_param*e_const/(2*k_B_const*Tl)) |
导带态密度 |
| Nv_param | Ni*exp(Eg0_param*e_const/(2*k_B_const*Tl)) |
价带态密度 |
| taun_param | 1e-6[s] | 电子寿命 |
| taup_param | taun_param | 空穴寿命 |
| bias | -4[V] | 器件偏压 |
| sweep | 1 | 偏压的扫描参数 |
相对介电常数:11.8 是硅的典型值
硅的带隙:1.12eV,温度升高时带隙会略微减小,但这里假定为常数
电子亲和能:4.05 eV 是硅的典型值
掺杂浓度:$N_a$与$N_d$两个值设为相等,说明这是一个对称的 P–N 结,简化分析
本征载流子浓度:纯硅在300K时电子与空穴的平衡浓度$1.25\times 10^{10} cm^{-3}$(典型值)
导带态密度与价带态密度:来自于统计力学近似
$$
n_i^2 = N_c N_v e^{-E_g / (kT)}
$$
在该模型中简化,将$N_c=N_v$,实际上取决于电子空穴有效质量
$$
N_c = 2 \left(\frac{2\pi m_n^* k T}{h^2}\right)^{3/2}\qquad N_v = 2 \left(\frac{2\pi m_p^* k T}{h^2}\right)^{3/2}
$$
一般来说在硅中$N_v/N_c \approx 0.37$
300K时的大概数值为
$$
N_c \approx 2.8 \times 10^{19} \mathrm{c m}^{-3} \qquad N_{v} \approx1 . 0 4 \times1 0^{1 9} \mathrm{c m}^{-3}
$$
局部变量
Kramer迁移率模型
列出电子的,空穴的类似
| 名称 | 表达式 | 描述 |
|---|---|---|
| A1n | 1430[cm^2/(V*s)] |
A1参数 |
| B1n | -2.2[1] |
B1参数(无量纲) |
| MUln | A1n*(Tl/300[K])^B1n |
MU1参数,晶格散射主导时电子的迁移率 |
| Ain | 4.61e17[1/(V*s*cm)] |
Ai参数(经验拟合常数) 描述掺杂浓度和温度对迁移率的影响 |
| Bin | 1.52e15[1/(K^2*cm^3)] |
Bi 参数(同Ai) |
| MUin | (Ain*(Tl/1[K])^(1.5)/Ntot)/(log(1+Bin*Tl^2/Ntot)-Bin*Tl^2/(Ntot+Bin*Tl^2)) |
MUi 参数,杂质散射的迁移率 |
| Xn | sqrt(6*MUln/MUin) |
X 参数,控制两种散射机制的权重关系 |
| mu_n | MUln*(1.025/(1+(Xn/1.68)^1.43)-0.025) |
电子迁移率,平滑函数,保证在两种散射机制之间过渡连续 |
| Ntot | semi.Naminus+semi.Ndplus |
电离杂质总数 |
1 | 温度 Tl → 晶格散射项 MUl |
操作
主要操作跟官方教程走就行,这里讲一下一些操作的原因
在半导体的设置窗口中,单击以展开离散化栏,从公式列表中选择有限元,对数公式(线性形函数)
当势能差很大(例如在P-N结耗尽区),电子或空穴浓度呈指数分布变化
普通有限元法若直接用线性形函数去近似 $n$ 与 $V$ 的空间分布,就会产生数值扩散或假振荡,因为线性插值函数无法精确捕捉指数曲线
对数公式是一种特殊的有限元离散方法,它在单元级的插值中对浓度采用了对数形式,使得在局部指数变化时仍能保持高精度和数值稳定性
对数有限元形式的线性形函数其实仍然使用一阶单元,但在离散时会对变量进行指数变换(或称对数平均),从而让电荷输运的对称性得到保持,不会因离散误差而破坏电流连续性
右键单击组件1 > 几何 1 并选择线段间隔
线段间隔决定了坐标轴上的区间范围,相当于设定了“模拟器件的物理尺寸”
每个间隔的端点会自动成为几何点,而这些点通常就是金属接触或电势边界的位置,所以线段间隔的定义也直接影响了后续边界条件的指定
插值
Kramer Eq V:平衡偏压(0 V)下的参考电势分布
Kramer Fwd V:正向偏压(+0.5 V)下的参考电势分布
Kramer Rev V:反向偏压(–4 V)下的参考电势分布
Kramer Eq n, Kramer Eq p 等:对应条件下电子与空穴浓度的参考分布
是用来导入文献参考结果的电势分布函数,以便将 COMSOL 的计算结果与理论或参考结果进行对比验证,像是一条真值曲线,用于测试模型是否解得正确
在定义工具栏中单击非局部耦合,然后选择积分
相当于做了一个基准电势归零的操作,让电势曲线的零点始终在边界1处,从而得到相对电势分布
定位到迁移率模型,从列表中选择用户定义,输入”mu_n” “mu_p”
变为变量,不再是常量,迁移率就会随着温度场或掺杂分布变化而自动更新
陷阱辅助复合
硅类半导体载流子复合的主要物理机制,在直接带隙材料(如GaAs)中,电子和空穴可以通过辐射复合(直接跃迁),但在硅这类间接带隙材料中,这种直接跃迁的概率非常低
复制半导体(semi)
方便后面添加第二个研究,不冲突
研究展开研究扩展栏,选中辅助扫描复选框,从扫描类型列表中选择所有组合,添加
| 参数名称 | 参数值列表 | 参数单位 |
|---|---|---|
| bias(器件偏压) | -4 0 0.5 | V |
| sweep(逐渐提高偏压的扫描参数) | 0 1 |
这是给有限元法准备的扫描参数,在后续选择不同电压条件的时候需要考虑第一个还是最后一个
在线结果图的设置窗口中, 定位到 x 轴数据栏,从参数列表中选择表达式,在表达式文本框中键入“x”
默认可能是参数值或者索引,需要把表达式改成x,让COMSOL以几何坐标为横轴绘制物理分布
(原来图上范围为0-5,改完之后变为-2.5~2.5)
图例改成FE是因为FE是有限元法的简称
结果>电势节点,然后单击线结果图1,y轴数据栏在表达式文本框中键入“V-intop1(V)”
把整个器件的电势分布减去某个积分算出来的参考电位,从而得到相对电势
V :电势场,从物理场中求解所得
intop1(...) :积分算符,在定义阶段创建的“非局部耦合>积分”节点生成的,换算成为相对电势
添加研究
为了比较有限元对数形式与有限体积法,需要更改离散方法,并添加第二个研究,用新的选择重新求解模型
FVM内置了物理导向的指数插值,对电势差的敏感性比 FEM 小得多,不需要电压逐渐升高,因此Va的期望值可以直接在辅助扫描中设置
| 参数名称 | 参数值列表 | 参数单位 |
|---|---|---|
| Va (外加电压) | -4 0 0.5 | V |
在后续选择不同电压条件的时候使用列表索引
添加线结果图3、4、5
引入参考文献插值解用于对比结果
GaAs光电二极管
模型定义
模拟一个简单的矩形砷化镓 PIN 结构,顶面上有一个 p 型接触,在底面上有一个 n 型接触
顶部是p⁺ – p – i 结构,底部是 n – n⁺ 结构,中间约0.7$\mu m$为本征层
由于导带和价带的倾斜特性:导带能量在 p 接触端最高,在 n 接触端最低
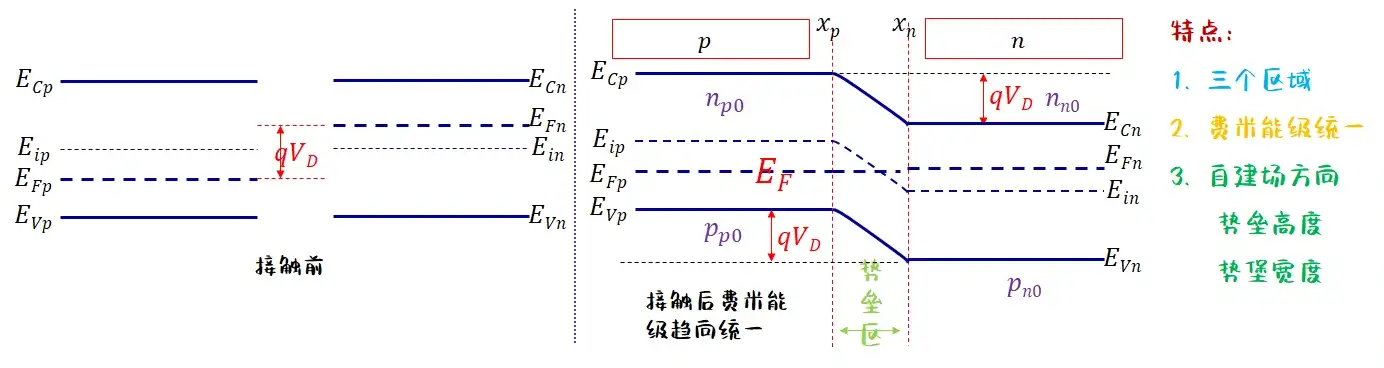
当一个光子被吸收并产生电子—空穴对时,电子会被电场驱动向 n 接触端运动,而空穴则朝相反方向移动到 p 接触端
在该结构中,p 接触端接地,n 接触端施加 2 V 电压,使其处于反向偏置状态(reverse bias)
对于给定波长的入射光,输出电流与光照强度成线性关系
反向偏置不仅会增大能带的倾斜度,还会扩大耗尽层的宽度,从而缩短响应时间,但这也会增加暗电流
半导体接口用于定义器件的掺杂分布和电接触区域
电磁波,频域接口用于定义入射的电磁辐射
光跃迁节点配置两个接口之间的耦合
该模型采用直接带隙模型来计算吸收过程,对于本模型所使用的 GaAs 材料而言,这是一种合理的近似
利用材料内电子空穴对的自发复合寿命,确定导带与价带中具有相同波矢状态的相互作用强度,从而计算自发辐射和受激辐射
频域计算通过引入一个额外的维度来表示,从而可以将某些特性可视化为光子能量的函数,这使得可以绘制自发辐射光谱
光子的吸收不仅在载流子连续性方程中引入了电子和空穴的生成项,还会引起材料极化率的变化
在模型构建树中的多物理场节点下,通过“半导体-电磁波耦合”实现两个接口的自动耦合,将电磁波频域接口中计算得到的电场用作半导体接口中吸收过程的输入,同时根据半导体接口计算出的结果修正电磁波接口中的材料极化率,以反映由载流子行为引起的变化
模型中执行波长扫描,其中入射光的功率保持恒定,波长范围为 875 nm 到 475 nm
砷化镓材料的带隙为1.424 eV,相当于约 872 nm 的波长
参数设置
二维模型,请特别注意涉及面外厚度的参数
| 名称 | 表达式 | 描述 |
|---|---|---|
| w_dom | 5[um] | 宽度 |
| h_dom | 1[um] | 厚度 |
| V_n | 2[V] | n 型接触电压 |
| V_p | 0[V] | p 型接触电压 |
| hbar0 | h_const/(2*pi) | 无弧度单位的hbar |
| lda0 | 870[nm] | 入射波长 |
| f0 | c_const/lda0 | 入射频率 |
| omega0 | 2*pi*1[rad]*f0 |
入射角频率 |
| E_ph | f0*h_const | 入射光子能量 |
| n0 | 3.5 | GaAs折射率(实部) |
| tau | 2[ns] | 自发寿命 |
| d0 | 1[um] | 半导体接口的面外厚度 (波动光学接口中默认为 1 m) |
| Pin | 10[uW] | 面外厚度 d0 = 1 um 时的入射功率 |
波长:870nm,光子能量约为1.425eV,接近带隙,吸收/反射都会很敏感
面外厚度:在二维仿真中,功率单位通常是W/m,引入一个面外厚度使得入射功率可以换算为总功率
自发寿命:代表电子–空穴对平均存在的时间,寿命越长,复合速率越低,说明材料缺陷较少或复合为辐射型,2ns是GaAs的典型辐射寿命
操作
设置掺杂
解析掺杂模型:用数学函数在器件内部定义“本底掺杂”以及主体的 p 区 / n 区的掺杂分布(例如常数、线性、指数或高斯型),常用于描述器件的主体结结构和掺杂梯度
几何掺杂模型:直接在几何区域上画上高掺杂层(例如在器件顶部/底部靠近金属的那一层做 p⁺ / n⁺),用于模拟为了改善金属接触而刻意做的极浅/薄高掺杂层
三个p掺杂区
定义从器件上方(金属接触)到内部的三个连续区域
恒定的 p 型掺杂 → 主体 p 区(保证耗尽区宽度与光吸收)
解析掺杂模型,浓度$N_{A0}=1\times 14cm^{-3}$(较低),代表p主体层或i区延伸部分
p 型掺杂 → 渐变过渡层(连接主体与接触)
解析掺杂模型,浓度提高到$N_{A0}=1\times 18cm^{-3}$,用来建立结区电场的 p 侧
从
(0,0.9*h_dom)开始(顶部10%),与主体层形成一个平滑的掺杂过渡$d_j$代表扩散过渡区域的厚度,用于平滑边界
p⁺ 型掺杂 → 高掺杂接触层(实现低阻欧姆接触)
几何掺杂模型,浓度提高到$N_{A0}=1\times 20cm^{-3}$,属于极高掺杂层
用于与金属接触形成欧姆接触,被定义在器件最上方、厚度约
0.1h_dom的区域
五个掺杂区
| 区域 | 类型 | 掺杂浓度 | 模型类型 |
|---|---|---|---|
| 恒定的 p 型掺杂 | 受主 | 1e14 cm⁻³ | 解析(背景 p) |
| p 型掺杂 | 受主 | 1e18 cm⁻³ | 解析(主体 p) |
| p⁺ 型掺杂 | 受主 | 1e20 cm⁻³ | 几何(接触层) |
| n 型掺杂 | 施主 | 1e18 cm⁻³ | 解析(主体 n) |
| n⁺ 型掺杂 | 施主 | 1e20 cm⁻³ | 几何(接触层) |
中间的 i 区是几乎未掺杂或极轻 p 型,用恒定的 p 型掺杂表示背景掺杂就足够,不需要恒定n型掺杂
材料折射率虚部设为0
在电磁学中
$$
\tilde{n}=n+i \kappa
$$
实部决定光传播速度(折射);虚部$\kappa$决定光吸收
在这个 PIN 光电二极管模型中,光吸收不是通过折射率虚部来建模的,而是由半导体物理接口自身的“光跃迁”节点计算得到的,再设一个非零虚部,反而会重复计算吸收,所以这里设为0
从求解的电场分量列表中选择面外矢量
因为模型是二维(x–y 平面)的,实际的光沿y传播方向
为了在二维模型中表示一个三维平面波的传播,电场当作面外分量(z方向震荡)
这是一种常见的简化,称为 TE 模式(横电模式)
边界 1 和 4 设置为“周期性条件”
由于模型是二维的(只考虑垂直方向变化),相当于假设在水平方向上无限延伸,这样光场不会在侧边泄露,也避免了侧壁反射
映射分布设置
边界3上设为1保持水平方向一致,边界1上设为500表示y方向分为500区间来分析
积分1的定义
非局部积分耦合,在整个半导体域上对各种物理量进行积分
绘图参数
semi.Nd —— 表示施主掺杂浓度
semi.Na —— 表示受主掺杂浓度
因为x轴反转弧长了,所以在绘图时y是从顶部开始



