FunRec推荐系统_召回模型
datawhalechina/fun-rec:推荐系统入门
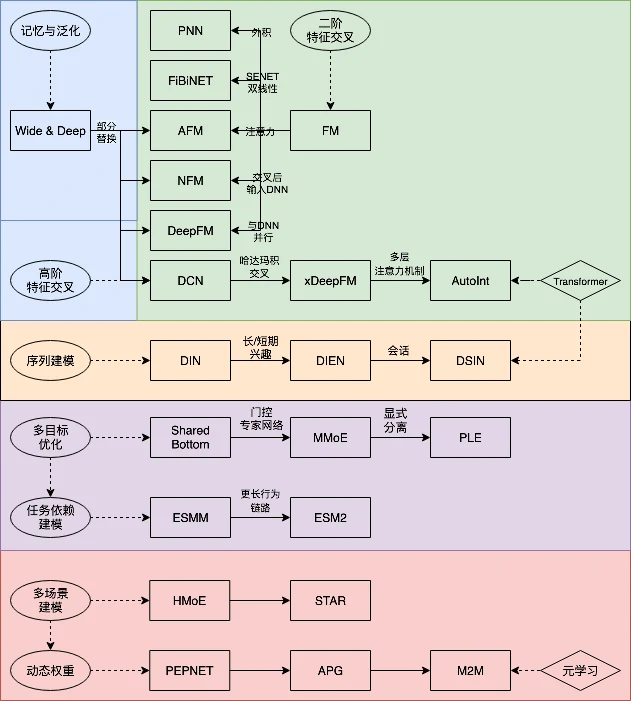
推荐系统
推荐系统的本质,是对关系的量化预测
预测过程需要系统深入理解三个关键要素
- 理解用户:历史记录,喜欢与不喜欢,搜索关键词
- 理解物品:对视频而已,内容属性:时长,制作质量;统计属性:多少人看过,平均评分
- 理解场景:比如一个在地铁上通勤的用户更可能对短视频感兴趣,而在家中休闲的用户则可能愿意观看较长的深度内容
将推荐系统的核心抽象为一个数学函数:接收对用户、物品和场景的理解作为输入,输出一个代表连接可能性的分数
在理想情况下,可以为每个用户计算与所有物品的匹配分数,然后简单地选择分数最高的几个进行推荐,但在真实的工业环境中,这种做法完全不可行
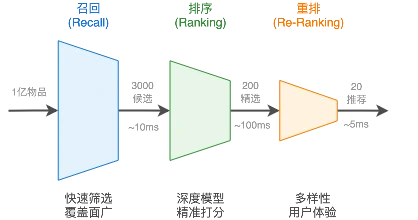
推荐系统工程化面临的核心矛盾:如何在极有限的时间内,从海量的候选中找到最优的推荐结果?
工业界的解决方案是采用分阶段的漏斗式架构,通过“召回-排序-重排”的三层流水线来逐步缩小候选范围,在效率和效果之间找到平衡点
- 召回:不追求高精度而强调覆盖面,利用少量特征,通过协同过滤快速找到品味相似的用户并推荐其偏好内容;或基于内容相似度,召回与近期观看视频相似的内容
- 排序:在召回后候选集极大缩小,这时使用预测函数,融合用户、物品、场景的所有可用特征,为每个候选物品计算精确的预测分数
- 重排:预测分数最高的列表,不一定等于用户体验最佳的列表,考虑多样性、新颖性、公平性等因素,也有可能插入广告等
召回系统:
排序系统:
指标:
hit_rate@K:对每个用户,真实物品出现在 Top-K 的比例HitRate@K = 被命中的用户数/总用户数
precision@K:对每个用户,Top‑K 推荐中属于真实正样本的比例Precision@K = Top-K 中相关物品数/K
ndcg@K:排得越靠前,得分越高
| 指标 | 关心点 | 是否看排序 | 适合评估什么 |
|---|---|---|---|
| HitRate@K | 有没有命中 | ❌ | 召回覆盖能力 |
| Precision@K | 命中比例 | ❌ | 推荐列表纯度 |
| NDCG@K | 排名质量 | ✅ | 排序是否合理 |
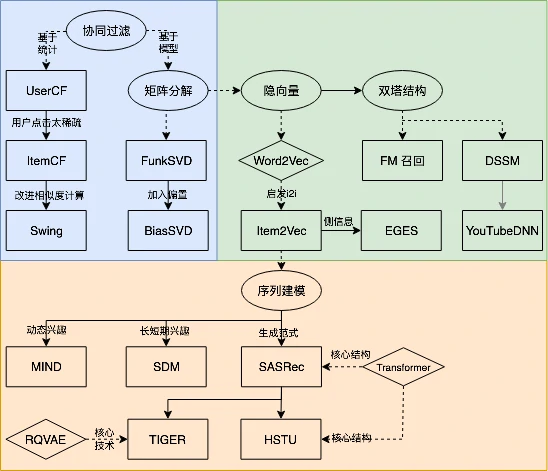
召回模型
协同过滤:基于用户或物品相似性进行建模,包括 ItemCF(含Swing)、UserCF、矩阵分解(向量化表示,含FunkSVD/BiasSVD)
向量召回:把用户和物品映射到向量空间,用向量检索完成大规模召回,包括双塔(DSSM)、YouTube DNN、EGES
序列召回:把用户看成随时间演化的状态,用最近行为预测下一步
协同过滤
核心思想基于一个朴素的假设:相似的用户会喜欢相似的物品
首先收集用户的历史行为数据(如评分、点击、购买记录),然后计算用户之间或物品之间的相似度,最后基于这些相似度为用户生成推荐
根据计算相似度的对象不同,协同过滤可以分为两种基本类型(邻域法):
基于物品的协同过滤(Item-based CF):推荐与用户历史偏好物品相似的其他物品
ItemCF在工业界应用广泛,因物品规模更小、属性更稳定,维护成本较低
Swing 算法利用用户-物品二部图结构提升相似度计算的鲁棒性,是 ItemCF 的改进方法
基于用户的协同过滤(User-based CF):寻找兴趣相似的用户并推荐其喜欢的物品
UserCF能够挖掘潜在兴趣、提升新颖性,但受限于用户规模大、兴趣变化快和行为稀疏等问题,在工业场景中应用受限
矩阵分解(Matrix Factorization, MF):现代CF,直接建模用户-物品交互矩阵,通过学习用户和物品的低维向量表示来预测偏好,实现了U2I的直接召回,属于模型法协同过滤,为后续向量召回奠定基础
ItemCF
ItemCF的思路建立在一个简单的假设上:用户的兴趣具有一定的连贯性,喜欢某个物品的用户往往也会对相似的物品感兴趣
实现流程主要包含两个步骤
步骤一:物品相似度计算
在大多数实际应用场景中通常只有用户是否对物品有过交互行为的数据(如点击、购买、收藏等),而没有具体的评分信息
理论上可以将每个物品表示为一个向量,然后计算向量间的相似度,但当商品数量巨大时,计算所有物品对之间的相似度会变成一个巨大的工程,时间复杂度达到$O(|I|^2)$
因此从用户出发找物品组合,采用更高效的实现方式:
构建用户-物品倒排表:为每个用户维护一个交互过的物品列表
计算物品共现矩阵:创建一个矩阵$C[i][j]$来记录物品$i$和$j$的共同用户数量
计算最终相似度:使用余弦相似度公式计算物品相似度
$$
w_{ij} = \frac{C[i][j]}{\sqrt{|N(i)| \cdot |N(j)|}}
$$
$|N(i)|$表示与物品$i$有交互的用户总数,分母是对共同用户数的标准化,防止热门商品占据绝对优势
$C[i][j]$是两个物品的共现次数
算法复杂度分析
相比暴力计算有显著的效率提升:
- 暴力方法:遍历$|U|$个用户,$O(|I|^2 \cdot |U|)$
- 优化方法:每个用户交互$|N(u)|$个物品,只计算有共同用户的物品对,$O(\sum_{u} |N(u)|^2)$
定义$\sum_{u} |N(u)| = R$(总交互数),且用户平均交互物品数$\bar{m} = R/|U|$,那么$\sum_{u} |N(u)|^2\approx \sum_{u} \bar m^2 = |U|\cdot \bar m^2$
总复杂度可以表示为$O(R \cdot \bar{m})$
现实推荐数据的典型特征:
- $\bar m\ll|I|$(用户只看极少数物品)
- 交互矩阵极度稀疏
优化方法效率远高于暴力计算,只计算真正有意义的物品对,避免了大量无效计算
步骤二:候选物品推荐
获得物品相似度矩阵后就可以预测用户对未接触物品的喜好程度了
选取用户最近交互的物品作为兴趣种子,为每个种子物品找到最相似的若干个候选物品,快速生成大量候选集合
用用户$u$过去看过的所有物品$j\in N(u)$,按它们和目标物品 $i$ 的相似度加权,得到用户对物品 $i$ 的兴趣评分
$$
\color{red} p(u, i) = \sum_{j \in N(u)} w_{ij} \cdot r_{uj}
$$
$w_{ij}$是物品之间的相似度,$r_{uj}$表示用户对物品$j$的兴趣强度(可以是简单的1,也可以根据交互时间、类型等设置不同权重)
最终系统对所有候选物品按兴趣分数排序,选择Top-N物品作为ItemCF通道的推荐结果
拓展:处理评分数据的相似度计算
余弦相似度适用于隐式反馈场景(如点击、浏览),但在某些应用中还有显式评分数据(如5星评分、点赞数等),对于这类数据,可以使用更精细的相似度计算方法
当有评分数据时,皮尔逊相关系数能更好地捕获物品间的相似性模式:
$$
w_{ij} = \frac{\sum_{u \in U_{ij}}(r_{ui} - \bar r_i)(r_{uj} - \bar r_j)}{\sqrt{\sum_{u \in U_{ij}}(r_{ui} - \bar r_i)^2}\sqrt{\sum_{u \in U_{ij}}(r_{uj} - \bar r_j)^2}}
$$
- $U_{ij}$:同时给物品 $i$ 和 $j$ 打过分的用户
- $r_{ui}$:用户 $u$ 对物品 $i$ 的评分
- $\bar r_i$:物品 $i$ 的平均评分
核心优势:皮尔逊相关系数通过中心化处理,能够
- 消除不同物品评分分布的差异(有些物品普遍评分高,有些偏低)
- 关注用户评分的相对趋势而非绝对数值
- 更好地识别“用户对两个物品评分模式一致”的相似性
基于皮尔逊相似度,可以预测用户对未接触物品的评分:
$$
\hat r_{u,j} = \bar r_j + \frac{\sum_{k \in S_j} w_{jk},\left( r_{u,k} - \bar r_{k} \right)}{\sum_{k \in S_j} w_{jk}}
$$
虽然皮尔逊在理论上更“优雅”,但在大规模系统中有问题:
- 计算复杂,需要均值、平方、归一化,且对每个物品对都要算
- 对稀疏数据不稳定,$U_{ij}$很小,相关系数噪声大
工业界更常见的是简化的余弦相似度,并通过其他方式(如加权、归一化)来处理评分差异
举例
预测用户1对物品5的评分
| 用户1 | 用户2 | 用户3 | 用户4 | 用户5 | |
|---|---|---|---|---|---|
| 物品1 | 5 | 3 | 4 | 3 | 1 |
| 物品2 | 3 | 1 | 3 | 3 | 5 |
| 物品3 | 4 | 2 | 4 | 1 | 5 |
| 物品4 | 4 | 3 | 3 | 5 | 2 |
| 物品5 | ? | 3 | 5 | 4 | 1 |
以计算物品5和1之间的相似度为例
$$
\bar r_{item5} = (3+5+4+1)/4=3.25 \\
\bar r_{item1} = (3+4+3+1)/4 = 2.75
$$
向量减去均值
$$
\text{item5}:(-0.25, 1.75, 0.75, -2.25) \quad \text{item1}: (0.25, 1.25, 0.25, -1.75)
$$
计算皮尔逊相似度
$$
\text{sim}(item5,item1)=\cos((-0.25, 1.75, 0.75, -2.25),(0.25, 1.25, 0.25, -1.75))=0.96946
$$
计算物品间的相似度矩阵
1
2
3
4
5
6
7
8import numpy as np
item_data = {
'item1': {'user1': 5, 'user2': 3, 'user3': 4, 'user4': 3, 'user5': 1},
'item2': {'user1': 3, 'user2': 1, 'user3': 3, 'user4': 3, 'user5': 5},
'item3': {'user1': 4, 'user2': 2, 'user3': 4, 'user4': 1, 'user5': 5},
'item4': {'user1': 4, 'user2': 3, 'user3': 3, 'user4': 5, 'user5': 2},
'item5': {'user2': 3, 'user3': 5, 'user4': 4, 'user5': 1},
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22import pandas as pd
similarity_matrix = pd.DataFrame(
np.identity(len(item_data)), # 生成一个 n × n 的单位矩阵
index=item_data.keys(),
columns=item_data.keys(),
)
# 遍历每条物品-用户评分数据
for i1, users1 in item_data.items():
for i2, users2 in item_data.items():
if i1 == i2: # 跳过同一个物体
continue
vec1, vec2 = [], []
for user, rating1 in users1.items():
rating2 = users2.get(user, -1) # 判断是否用户是否也打过分
if rating2 == -1:
continue
vec1.append(rating1)
vec2.append(rating2)
similarity_matrix[i1][i2] = np.corrcoef(vec1, vec2)[0][1]
print(similarity_matrix)1
2
3
4
5
6item1 item2 item3 item4 item5
item1 1.000000 -0.476731 -0.123091 0.532181 0.969458
item2 -0.476731 1.000000 0.645497 -0.310087 -0.478091
item3 -0.123091 0.645497 1.000000 -0.720577 -0.427618
item4 0.532181 -0.310087 -0.720577 1.000000 0.581675
item5 0.969458 -0.478091 -0.427618 0.581675 1.000000从user1交互过的物品中,找到与item5最相似的2个物品
1
2
3
4
5
6target_user = 'user1'
target_item = 'item5'
num = 2
sim_items = similarity_matrix[target_item].sort_values(ascending=False)[1:num+1].index.tolist()
print(f'与物品{target_item}最相似的{num}个物品为:{sim_items}')1
与物品item5最相似的2个物品为:['item1', 'item4']
预测用户1对物品5的评分
1
2
3
4
5
6
7
8
9
10
11
12
13
14target_user_mean_rating = np.mean(list(item_data[target_item].values()))
weighted_scores = 0.
corr_values_sum = 0.
for item in sim_items:
corr_value = similarity_matrix[target_item][item]
user_mean_rating = np.mean(list(item_data[item].values()))
weighted_scores += corr_value * (item_data[item][target_user] - user_mean_rating)
corr_values_sum += corr_value
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
print(f'用户{target_user}对物品{target_item}的预测评分为:{target_item_pred}')1
用户user1对物品item5的预测评分为:4.6
1 | from funrec import run_experiment |
数据集:ml-latest-small,仅用ratings.csv,输入userId,movieId以及rating
用 rating_threshold 过滤正样本,只保留正反馈,生成二元标签 label=1
1 | +---------------+--------------+----------------+---------------+ |
Swing
ItemCF 虽然简单有效,但在工业场景中存在明显不足:热门物品因高频占据主导,随机点击等噪声行为会干扰相似度计算,且不同类型的用户行为被一视同仁,难以区分真实兴趣与偶然行为,也无法刻画物品的替代性和互补性关系
Swing 算法从用户–物品二部图结构出发,不再单纯依赖共现次数,而是通过挖掘更具鲁棒性的共同购买关系来过滤噪声,更准确地刻画物品之间的真实关联,实现可以分为两个主要步骤:
步骤一:用户-物品二部图构建
首先将用户与物品的交互数据转化为一个二部图,一边是所有用户节点,另一边是所有物品节点,如果用户对某个物品发生了点击、购买等行为,就在对应的用户节点与物品节点之间添加一条边,为后续的相似度计算提供了结构化的数据基础
步骤二:物品相似度计算
计算任意一对物品 $ i $ 与 $ j $ 的相似度
设 $ U_{i} $ 和 $ U_{j} $ 分别表示与物品 $ i $ 和 $ j $ 有过交互的用户集合,$I_{u}$表示用户$ u $交互过的所有物品集合
首先找到同时与物品 $ i $ 和 $ j $ 相连的用户集合 $ U_{i} \cap U_{j} $,然后对集合中的每一对用户$(u, v)$统计他们的其他共同购买行为,如果用户 $ u $ 与 $ v $ 的其他交互行为重合较少(即 $ \left|I_{u} \cap I_{v}\right| $ 较小),则认为他们在共同选择物品 $ i $ 和 $ j $ 上的行为更具特异性,应该为这对物品贡献更高的相似度得分
Swing score 的基础计算公式为:
$$
s(i, j) = \sum_{u \in U_i \cap U_j} \sum_{v \in U_i \cap U_j} \frac{1}{\alpha + |I_u \cap I_v|}
$$
其中$\alpha$是平滑系数,用来防止分母过小导致数值不稳定
一个具体例子:
用户$A,B,C$,物品$h,t,r,p$

假设$\alpha = 1$,看用户与物品之间的连线计算数量
- 用户对$[A, B]$的贡献分数为$\frac{1}{1 + 4} = \frac{1}{5}$
- 用户对$[B, C]$的贡献分数为$\frac{1}{1 + 2} = \frac{1}{3}$
- 用户对$[A, C]$的贡献分数为$\frac{1}{1 + 2} = \frac{1}{3}$
物品$h,p$交集有$[A, B]$,$[A, C]$,$[B,C]$,所以swing score为 $s(h, p) = \frac{1}{5} + \frac{1}{3} + \frac{1}{3} = \frac{13}{15}$
物品$h,t(r)$的交集只有用户对$[A, B]$,所以swing score为 $s(h, t) = s(h, r) = \frac{1}{5}$
用户权重调整
为了降低活跃用户对计算结果的过度影响引入用户权重$w_u = \frac{1}{\sqrt{|I_u|}}$,控制单个节点(用户)在图结构中的能量输出规模
最终公式为
$$
\color{red} s(i, j) = \sum_{u \in U_i \cap U_j} \sum_{v \in U_i \cap U_j} w_u \cdot w_v \cdot \frac{1}{\alpha + |I_u \cap I_v|}
$$
Swing算法的核心在于Swing Score的计算,它通过分析用户-物品二部图中的swing结构来度量物品相似度
1 | def calculate_swing_similarity(item_users, user_items, user_weights, item_i, item_j, alpha=1.0): |
1 | run_experiment('swing') |
1 | +---------------+--------------+----------------+---------------+ |
UserCF
UserCF基于一个简单假设:具有相似历史行为的用户,未来偏好也相似
尽管实践中更偏向 ItemCF,但 UserCF 提出的用户向量化思想为后续的矩阵分解模型奠定了基础
实现过程可以分解为两个核心步骤
步骤一:用户相似度计算
假设用户$u$和用户$v$分别对应物品集合$N(u)$和$N(v)$(即他们各自有过行为的物品)
杰卡德相似系数:
如果系统只记录用户是否对物品有过行为(比如是否点击、购买),而没有具体的评分,这个系数是个不错的选择
$$
w_{uv} = \frac{|N(u) \cap N(v)|}{|N(u) \cup N(v)|}
$$
分子是两人共同喜欢的物品数量,分母是两人喜欢的物品总数(去重后)
余弦相似度:
将每个用户看成一个向量,计算向量间的夹角
$$
w_{uv} = \frac{|N(u) \cap N(v)|}{\sqrt{|N(u)|\cdot|N(v)|}}
$$
余弦相似度已经考虑了用户活跃度的差异
皮尔逊相关系数
有评分数据时
$$
w_{uv} = \frac{\sum_{i \in I}(r_{ui} - \bar r_u)(r_{vi} - \bar r_v)}{\sqrt{\sum_{i \in I}(r_{ui} - \bar r_u)^2}\sqrt{\sum_{i \in I}(r_{vi} - \bar r_v)^2}}
$$
和之前ItemCF不一样的是,这里的平均数计算的是每个用户的
皮尔逊系数通过中心化处理,有效消除了个人评分习惯的差异
通常选择相似度最高的K个用户作为“邻居”
步骤二:候选物品推荐
有了相似用户,下一步就是利用他们的偏好来预测目标用户对未交互过的物品的兴趣
简单加权平均
$$
\hat r_{u,p} = \frac{\sum_{v \in S_u} w_{uv} , r_{v,p}}{\sum_{v \in S_u} w_{uv}}
$$
$\hat r_{u,p}$是预测的用户$u$对物品$p$的评分,$S_u$是邻居用户集合,$w_{uv}$是相似度权重,$r_{v,p}$是邻居$v$对物品$p$的实际评分
如果考虑消除个人评分习惯影响可以加入偏置修正
$$
\hat r_{u,p} = \bar r_{u} + \frac{\sum_{v \in S_u} w_{uv} , (r_{v,p} - \bar r_{v})}{\sum_{v \in S_u} w_{uv}}
$$
优化策略
UserCF看起来很简单,但有个类似物品对的问题:当用户数量很大时,计算所有用户对之间的相似度会非常耗时,时间复杂度达到$O(|U|^2)$,同样的思路构建物品倒排表
- 构建倒排表:为每个物品维护一个用户列表,记录哪些用户对这个物品有过行为,这样就可以通过物品快速找到相关用户
- 稀疏矩阵计算:创建一个矩阵$C[u][v]$来记录用户$u$和$v$的共同物品数量
- 计算最终相似度:矩阵给出了余弦相似度公式的分子,再除以分母$\sqrt{|N(u)||N(v)|}$得到了用户相似度
- 线上召回
召回的具体过程:系统为目标用户找到最相似的K个用户作为“相似用户集合”(通常K=50-200),收集这些相似用户交互过的所有物品作为候选集合,并计算目标用户对候选物品的兴趣分数
$$
p(u, i) = \sum_{v \in S_u \cap N(i)} w_{uv} \cdot r_{vi}
$$
这里的计算和ItemCF一样,不再多赘述
优化后的时间复杂度约为$O(R \cdot \bar n)$,其中$R$是总的用户-物品交互记录数,$\bar n$是每个物品的平均用户数
举例
| 物品1 | 物品2 | 物品3 | 物品4 | 物品5 | |
|---|---|---|---|---|---|
| 用户1 | 5 | 3 | 4 | 4 | ? |
| 用户2 | 3 | 1 | 2 | 3 | 3 |
| 用户3 | 4 | 3 | 4 | 3 | 5 |
| 用户4 | 3 | 3 | 1 | 5 | 4 |
| 用户5 | 1 | 5 | 5 | 2 | 1 |
基于皮尔逊相关系数,计算用户1与用户2的相似度
$$
\bar r_{user1}=4,\ \bar r_{user2}=2.25 \rightarrow \text{user1}:(1,-1, 0,0) \quad \text{user2}: (0.75,-1.25,-0.25,0.75)
$$
计算这俩新向量的余弦相似度,得到皮尔逊相似度$0.852$
根据相似用户,用户2对物品5的评分是3,用户3对物品5的打分是5,可以计算出 用户1 对物品5的最终得分是
$$
P_{user1, item5}=\bar r_{user1}+\frac{\sum_{k=1}^{2}\left(w_{user1,user k}\left(r_{userk, item5}-\bar r_{userk}\right)\right)}{\sum_{k=1}^{2} w_{user1, userk}}=4+\frac{0.85*(3-2.4)+0.7*(5-3.8)}{0.85+0.7}=4.87
$$
数据准备
1
2
3
4
5
6
7
8import numpy as np
user_data = {
'user1': {'item1': 5, 'item2': 3, 'item3': 4, 'item4': 4},
'user2': {'item1': 3, 'item2': 1, 'item3': 2, 'item4': 3, 'item5': 3},
'user3': {'item1': 4, 'item2': 3, 'item3': 4, 'item4': 3, 'item5': 5},
'user4': {'item1': 3, 'item2': 3, 'item3': 1, 'item4': 5, 'item5': 4},
'user5': {'item1': 1, 'item2': 5, 'item3': 5, 'item4': 2, 'item5': 1},
}使用字典来建立用户-物品的交互表
由于现实场景中,用户对物品的评分比较稀疏,如果直接使用矩阵进行存储,会存在大量空缺值,故此处使用了字典
基于皮尔逊相关系数,计算用户相似性矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24# 初始化相似性矩阵
import pandas as pd
similarity_matrix = pd.DataFrame(
np.identity(len(user_data)),
index=user_data.keys(),
columns=user_data.keys(),
)
# 遍历每条用户-物品评分数据
for u1, items1 in user_data.items():
for u2, items2 in user_data.items():
if u1 == u2:
continue
vec1, vec2 = [], []
for item, rating1 in items1.items():
rating2 = items2.get(item, -1)
if rating2 == -1:
continue
vec1.append(rating1)
vec2.append(rating2)
# 计算不同用户之间的皮尔逊相关系数
similarity_matrix[u1][u2] = np.corrcoef(vec1, vec2)[0][1]
print(similarity_matrix)1
2
3
4
5
6user1 user2 user3 user4 user5
user1 1.000000 0.852803 0.707107 0.000000 -0.792118
user2 0.852803 1.000000 0.467707 0.489956 -0.900149
user3 0.707107 0.467707 1.000000 -0.161165 -0.466569
user4 0.000000 0.489956 -0.161165 1.000000 -0.641503
user5 -0.792118 -0.900149 -0.466569 -0.641503 1.000000计算用户1最相似的n个用户
1
2
3
4
5target_user = 'user1'
num = 2
# 由于最相似的用户为自己,去除本身
sim_users = similarity_matrix[target_user].sort_values(ascending=False)[1:num+1].index.tolist()
print(f'与用户{target_user}最相似的{num}个用户为:{sim_users}')1
与用户user1最相似的2个用户为:['user2', 'user3']
预测用户1对物品5的评分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15weighted_scores = 0.
corr_values_sum = 0.
target_item = 'item5'
# 基于皮尔逊相关系数预测用户评分
for user in sim_users:
corr_value = similarity_matrix[target_user][user]
user_mean_rating = np.mean(list(user_data[user].values()))
weighted_scores += corr_value * (user_data[user][target_item] - user_mean_rating)
corr_values_sum += corr_value
target_user_mean_rating = np.mean(list(user_data[target_user].values()))
target_item_pred = target_user_mean_rating + weighted_scores / corr_values_sum
print(f'用户{target_user}对物品{target_item}的预测评分为:{target_item_pred:.4f}')1
用户user1对物品item5的预测评分为:4.8720
1 | from funrec import run_experiment |
1 | +---------------+--------------+----------------+---------------+ |
矩阵分解
UserCF 和 ItemCF 虽然直观易懂,但在真实场景中都会受到数据稀疏性的限制:大多数用户只与很少的物品发生过交互
这使得相似度既难以可靠计算,即便找到邻居,覆盖的物品也十分有限
邻域方法通常先计算相似度、再进行推荐,这种两阶段流程缺乏对整体交互数据的全局建模
转向另一种思路:不再显式计算相似度,而是通过学习用户和物品的隐向量表示,让相似性在向量空间中自然体现
矩阵分解正是这一思想的代表,也标志着协同过滤从传统统计方法走向机器学习方法
矩阵分解的核心想法建立在两个关键假设上:
- 低秩假设:看似复杂的评分矩阵实际上只由少数几个隐含因素主导,比如“面向男性vs面向女性”、“严肃vs逃避现实”等维度
- 隐向量假设:用户和物品都可以表示为这些隐含因素构成的向量,用户向量刻画偏好,物品向量刻画特征
基础模型FunkSVD
基本思想:把复杂的用户-物品评分矩阵分解成两个简单的矩阵——用户特征矩阵和物品特征矩阵
假设有$m$个用户和$n$个物品,想要用$K$个隐含因子来描述它们,那么用户$u$可以用一个$K$维向量$p_u$来表示,物品$i$也可以用一个$K$维向量$q_i$来表示,预测用户$u$对物品$i$的评分就是这两个向量的内积:
$$
\hat r_{ui} = p_u^T q_i = \sum_{k=1}^{K} p_{u,k} \cdot q_{i,k}
$$
$p_{u,k}$表示用户$u$在第$k$个隐含因子上的偏好程度,$q_{i,k}$表示物品$i$在第$k$个隐含因子上的特征强度
现在问题变成了:如何找到这些隐含因子?
采用一个很自然的思路——让预测评分尽可能接近真实评分,也就是要最小化所有已知评分的预测误差
$$
\min_{P,Q} \frac{1}{2} \sum_{(u,i)\in \mathcal{K}} \left( r_{ui} - p_u^T q_i \right)^2
$$
$\mathcal{K}$表示所有已知评分的用户-物品对,$r_{ui}$是用户$u$对物品$i$的真实评分
使用梯度下降法,先计算预测误差$e_{ui} = r_{ui} - p_u^T q_i$,然后沿着误差减小的方向更新参数:
$$
p_{u,k} \leftarrow p_{u,k} + \eta \cdot e_{ui} \cdot q_{i,k}\\
q_{i,k} \leftarrow q_{i,k} + \eta \cdot e_{ui} \cdot p_{u,k}
$$
在实际应用中通常还会加入L2正则化来防止过拟合
$$
\min_{P,Q} \frac{1}{2} \sum_{(u,i)\in \mathcal{K}} \left( r_{ui} - p_u^T q_i \right)^2 + \lambda \left( |p_u|^2 + |q_i|^2 \right)
$$
核心代码
FunkSVD的核心在于学习用户和物品的隐向量表示,使用Embedding层来表示这些隐向量,并通过内积计算预测评分:
1 | # === 用户塔 === |
embedding_dim对应公式中的隐含因子数量$K$
user_factors对应$p_u$,item_factors对应$q_i$
通过训练,模型会自动学习最优的隐向量表示,使预测评分尽可能接近真实评分
训练和评估
1 | from funrec import run_experiment |
数据集ml-1m_recall_pos_neg_data:来自ml-1m
- 正样本:用户在真实时间序列中下一次真实交互的电影
- 负样本:在保持用户历史不变的情况下,随机替换成的电影(可能没看过)
输入特征:user_id、movie_id(embedding dim=8)
训练loss = binary_crossentropy
用户/物品 embedding 做点积 + sigmoid 输出
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
- hit_rate@5/10:每个用户的真实正样本里,是否有被推荐进 Top‑K
- precision@5/10:Top‑K 推荐中真实正样本所占比例
- ndcg@5/10:考虑位置的排序指标(越靠前越高)
基本没有推荐上
改进模型BiasSVD
基础模型虽然简洁,但不同用户的评分习惯差异很大
BiasSVD在基础模型的基础上引入了偏置项,让预测公式变成:
$$
\hat r_{ui} = \mu + b_u + b_i + p_u^T q_i
$$
新增三个项
- $\mu$:所有评分的全局平均值,反映了整个系统的评分水平
- $b_u$:用户$u$的个人偏置,反映了该用户的打分习惯
- $b_i$:物品$i$的偏置,反映了该物品相对于平均水平是受欢迎还是不受欢迎
相应地,优化目标也要调整:
$$
\min_{P,Q,b_u,b_i} \frac{1}{2} \sum_{(u,i)\in \mathcal{K}} \left( r_{ui} - \mu - b_u - b_i - p_u^T q_i \right)^2 + \lambda \left( |p_u|^2 + |q_i|^2 + b_u^2 + b_i^2 \right)
$$
在参数更新时,除了用户和物品的隐向量,还需要更新偏置项
$$
b_u \leftarrow b_u + \eta \left( e_{ui} - \lambda b_u \right)\\
b_i \leftarrow b_i + \eta \left( e_{ui} - \lambda b_i \right)
$$
这种改进看似简单,但效果显著,通过分离出系统性偏差,模型能够更准确地捕捉用户和物品之间的真实交互模式,从而提供更精准的推荐
1 | # === 用户塔 === |
与FunkSVD相比,BiasSVD的关键区别在于:
- 用户和物品都增加了独立的偏置Embedding(
user_bias和item_bias) - 添加了全局偏置项(
global_bias),对应公式中的 $\mu$ - 最终预测使用
Add层将四个部分相加:$\mu + b_u + b_i + p_u^T q_i$
训练和评估
1 | run_experiment('biassvd') |
同样使用ml-1m_recall_pos_neg_data,输入user_id和movie_id
- 用户塔:
user_factors + user_bias(embedding) - 物品塔:
item_factors + item_bias(embedding) - 交互:
user_factors · item_factors - 预测:
global_bias + user_bias + item_bias + interaction - 最后接
sigmoid输出点击概率
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
相比刚刚的好一些
总结
| 方法 | 建模对象 | 相似性来源 | 学习方式 | 是否显式相似度 | 是否有向量表示 | 是否含 Bias | 主要解决什么问题 | 典型使用阶段 |
|---|---|---|---|---|---|---|---|---|
| UserCF | 用户–用户 | 用户行为重叠 | 统计共现 | 是 | 否 | 否 | 找兴趣相似的用户 | 教学 / 原型 |
| ItemCF | 物品–物品 | 物品被同一用户点击 | 统计共现 | 是 | 否 | 否 | 稳定、可缓存的相似物品 | 传统召回 |
| Swing | 物品–物品 | 高质量用户共现 | 加权统计 | 是(加权) | 否 | 否 | 稀疏数据下的相似度可靠性 | 大规模召回 |
| FunkSVD | 用户–物品 | 向量内积 | 优化目标学习 | 否 | 是 | 否 | 隐式兴趣建模、Embedding 召回 | Embedding 召回 |
| BiasSVD | 用户–物品 | 向量内积 + 偏置 | 优化目标学习 | 否 | 是 | 是 | 拟合系统性偏好、绝对打分 | 评分 / 精排 |
向量召回
矩阵分解奠定了推荐系统中向量化建模的基础,但矩阵分解是线性模型,表达能力有限,主要依赖用户–物品交互矩阵,在超大规模场景下面临数据稀疏以及计算与存储压力
向量召回延续矩阵分解的向量表示思想,用更复杂的模型(DNN)学习向量,融合多源特征,提升表达能力
加上NLP领域的嵌入(Embedding)技术,将离散符号映射到连续向量空间,向量距离具备语义意义(Word2Vec)
向量召回借鉴该思想,用户和物品共享向量空间,距离表示相似度,推荐问题转化为向量检索
向量召回技术主要沿着两条路径发展
- I2I(Item-to-Item)召回:用“物品向量”去检索“相似物品向量”
- U2I(User-to-Item)召回:用“用户向量”去检索“物品向量”
I2I召回
所有I2I召回方法的本质都是在回答同一个问题:如何更好地定义和利用“序列”来学习物品之间的相似性
Word2Vec
Word2Vec是序列建模的理论基础
主要包含两种模型架构:
- Skip-Gram:用中心词 → 预测上下文,对低频词更友好,推荐系统广泛采用 Skip-gram 视角
- CBOW(Continuous Bag of Words):用上下文 → 预测中心词,对高频词友好
Skip-Gram模型
给定文本序列中位置$t$的中心词$w_t$,模型的目标是最大化其上下文窗口内所有词语的出现概率
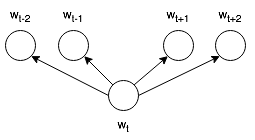
中心词$w_t$预测上下文词$w_{t+j}$的条件概率定义为(softmax格式)
$$
P(w_{t+j} | w_t) = \frac{e^{v_{w_{t+j}}^T v_{w_t}}}{\sum_{k=1}^{|V|} e^{v_{w_k}^T v_{w_t}}}
$$
其中$v_{w_i}$表示词$w_i$的向量表示,$V$是词汇表,分子中的内积$v_{w_{t+j}}^T v_{w_t}$衡量了中心词与上下文词的相似度
负采样优化
在 Word2Vec 中,直接计算 softmax 分母需要遍历整个词表,计算代价极高,为此引入了负采样(Negative Sampling)来进行优化,从多分类 → 多个二分类,其目标函数为:
$$
\color{red}\log \sigma(v_{w_{t+j}}^T v_{w_t}) + \sum_{i=1}^{k} \mathbb E_{w_i \sim P_n(w)} \log \sigma(-v_{w_i}^T v_{w_t})
$$
其中$\color{purple}\sigma(x) = \frac{1}{1 + e^{-x}}$是sigmoid函数(二分类问题常用),$k$是负样本数量,$P_n(w)$是负采样分布
负采样的直观解释是:对于真实的词对,希望增加它们的相似度;对于随机采样的负样本词对,希望降低它们的相似度
Item2Vec
Item2Vec(Barkan and Koenigstein, 2016)的核心洞察在于发现了用户行为数据与文本数据的结构相似性
在文本中,一个句子由多个词语组成,词语之间的共现关系反映了语义相似性
在推荐系统中,每个用户的交互历史可以看作一个“句子”,其中包含的物品就是“词语”
这种映射关系可以表示为:
- 词语 → 物品
- 句子 → 用户交互序列
- 词语共现 → 物品共同被用户交互
Item2Vec直接采用Word2Vec的Skip-Gram架构,但在序列构建上有所简化
给定数据集$\mathcal{S} = {s_1, s_2, \ldots, s_n}$,其中每个$s_i$包含用户$i$交互过的所有物品,Item2Vec将每个用户的交互历史视为一个集合而非序列,忽略了交互的时间顺序
优化目标函数与Word2Vec保持一致:
$$
\color{red}\mathcal L = \sum_{s \in \mathcal{S}} \sum_{l_{i} \in s} \sum_{-m \leq j \leq m, j \neq 0} \log P(l_{i+j} | l_{i})
$$
其中$l_i$表示物品,$m$是上下文窗口大小,$P(l_{i+j} | l_{i})$采用与Word2Vec相同的softmax形式计算
Item2Vec的实现可以直接调用gensim库(Řehůřek and Sojka, 2010)的Word2Vec模型,核心在于将用户交互序列作为训练语料,训练完成后,每个物品都得到一个稠密的向量表示
1 | from gensim.models import Word2Vec |
训练和评估
1 | from funrec import run_experiment |
数据集ml_latest_small_youtubednn:ml-latest-small 的 ratings.csv 与 movies.csv
将 ratings 与 movies 按 movieId 合并,得到包含 userId, movieId, genres, timestamp 的行为日志
基于该日志统计并构建 feature_dict,并按时间为每个用户构造历史序列hist_movie_id_list(语料库),训练集用滑窗生成多条序列样本,测试集取最后一次行为做评估
Item2Vec使用了序列形式的数据,但训练目标只关心是否共现,不关心先后顺序
U1:手机 → 手机壳 → 钢化膜 → 充电线 → 移动电源 (标准购买路径)
U2:手机 → 蓝牙耳机 → 手机壳 → 充电线 (跳跃 + 回退)
U3:手机 → 游戏手柄 → 电竞耳机 (冷启动 + 小众)
Item2Vec 会从所有序列中抽共现对
1 | (手机, 手机壳) |
顺序在模型中是弱化甚至被对称化的
Item2Vec 会倾向于把 手机壳 / 钢化膜 / 充电线 / 移动电源 拉得很近,把游戏手柄漂的比较远,小众兴趣被头部物品淹没
在config中embedding_external=True,训练不走TensorFlow 的 model.fit 监督流程,使用外部 embedding(gensim.Word2Vec)在序列上做自监督表示学习
通过 Word2Vec 学到每个 movieId 的向量表示,用户向量用其历史序列中物品向量的均值表示,推荐时用用户向量与全量物品向量计算相似度,取 Top‑K 作为召回结果并计算指标
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
EGES
Item2Vec 证明了序列建模在推荐系统中的有效性,但其设计较为简单,也存在明显不足
- 将用户行为视为无序集合,忽略时序信息,难以刻画真实的行为模式
- 严重依赖历史交互数据,面对新物品时无法学习有效表示
EGES(wang, 2018)针对这些问题进行了改进:
- 基于会话构建更精细的商品关系图,更准确地建模用户行为
- 引入商品的辅助信息,缓解冷启动问题
构建商品关系图
EGES的第一个创新是将物品序列的概念从简单的用户交互扩展为更精细的会话级序列
在固定时间窗口内,当两个商品在用户行为序列中连续出现时,便在它们之间建立一条有向边,其权重由该转移关系在所有用户历史中出现的频率决定
.webp)
相比将整个用户历史视为一个序列,这种基于会话的商品图能够更准确地刻画用户在短时间内的连续兴趣转移
在此基础上,EGES 在商品图上进行采用带权随机游走策略生成训练序列,转移概率由边权重决定:
$$
\begin{split}P(v_j|v_i) = \begin{cases}
\frac{M_{ij}}{\sum_{j=1}^{|N_+(v_i)|}M_{ij}} & \text{if } v_j \in N_+(v_i) \
0 & \text{if } e_{ij} \notin E
\end{cases}\end{split}
$$
其中$M_{ij}$表示节点$v_i$到节点$v_j$的边权重,$N_+(v_i)$表示节点$v_i$的邻居集合
通过随机游走过程,可以生成大量的商品序列用于后续的embedding学习
融合辅助信息解决稀疏性问题
引入商品的辅助信息(如类别、品牌、价格区间等)来增强商品的向量表示
GES的核心思想是将商品本身的Embedding与其各种属性的Embedding进行平均聚合
$$
H_v=\frac{1}{n+1} \sum_{s=0}^n{W_v^s}
$$
其中$W_v^s$表示商品$v$的第$s$种属性的向量表示,$W_v^0$表示商品ID的向量表示
这种方法虽然有效缓解了冷启动问题,但它假设所有类型的辅助信息对商品表示的贡献是相等的,这显然不符合实际情况
EGES的核心创新在于认识到不同类型的辅助信息应该有不同的重要性
对于具有$n$种辅助信息的商品$v$,EGES为其维护$n+1$个向量表示:一个商品ID的向量表示,以及$n$个属性的向量表示
商品的最终向量表示通过加权聚合得到
$$
H_v =\sum_{j}\left(\frac{e^{a_{v}^{j}}}{\sum_{k} e^{a_{v}^{k}}}\right) W_{v}^{j} = \frac{\sum_{j=0}^n e^{a_v^j} W_v^j}{\sum_{j=0}^n e^{a_v^j}}
$$
其中$a_v^j$是可学习的权重参数,这种设计体现了不同类型的辅助信息对不同商品的重要性
核心代码
EGES的核心在于商品特定注意力层(ItemSpecificAttentionLayer),它为每个商品学习一组特征权重
1 | def call(self, inputs, item_indices): |
这里的attention_weights是一个形状为$|V| \times (n+1)$的参数矩阵,其中$|V|$是商品总数,$n+1$特征数量(商品ID + $n$种辅助信息)
对于每个商品,模型会学习到一组特定的权重,自动发现哪些特征对该商品更重要,这种商品特定的注意力机制是EGES相比简单平均聚合的关键优势
冷启动商品的处理
对于无任何用户行为的新商品,既无法学习 item ID 向量,也没有对应的注意力权重
EGES 采用 mean pooling 策略,将商品的各类辅助特征向量(如类目、品牌、价格区间等)直接取平均,构造商品表示
虽然忽略了属性重要性的差异,但能有效利用内容信息,使冷启动商品仍可参与向量相似度召回
训练优化
EGES采用与Word2Vec类似的负采样策略,但损失函数经过了优化:
$$
\color{red}L(v,u,y) = -[y\log(\sigma(H_v^TZ_u)) + (1-y)\log(1-\sigma(H_v^TZ_u))]
$$
其中$y$是标签(1表示正样本,0表示负样本),这里仍然是自监督标签,不是人工标注
$H_v$是商品$v$的向量表示,$Z_u$是上下文节点$u$的向量表示,$H_v^TZ_u$衡量商品$v$和上下文商品$u$是否“应该有关联”
EGES在淘宝的实际部署效果显著
1 | run_experiment('eges') |
数据集ml-1m_recall_data:ml-1m下的 movies.dat
获得用户的历史序列 hist_movie_id
把历史序列当成图的路径 → 随机游走 → 得到 (movie_id, context_id)(正负样本对)
为什么EGES 不属于“序列召回”?
因为有向序列只是用于“构图”,不会作为模型输入序列去建模时间顺序
A → B → C → D 模型看到的只是 (A, B), (B, C), (C, D),路径结构在这里消失了,方向信息没有形成状态差异
同样的例子:
U1:手机 → 手机壳 → 钢化膜 → 充电线 → 移动电源 (标准购买路径)
U2:手机 → 蓝牙耳机 → 手机壳 → 充电线 (跳跃 + 回退)
U3:手机 → 游戏手柄 → 电竞耳机 (冷启动 + 小众)
EGES能够在购买手机后推荐游戏手柄,给出小众但合理的扩展
但和Item2Vec一样给出的都是静态 item embedding,无法知道现在处于什么阶段
genre_id 是 movie_id 对应的类别(从特征字典映射出来)
输入(movie_id, context_id, genre_id),把 movie_emb 和 genre_emb 组合成一个物品表示,并自动学习特征重要性,再用物品表示和 context_emb 做点积
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
Airbnb
Airbnb作为全球最大的短租平台,面临着与传统电商不同的挑战
房源不是标准化商品,用户的预订行为远比点击浏览稀疏,而且地理位置成为了一个关键因素
Airbnb需要的不仅仅是相似性,而是能够真正促进最终预订转化的推荐,其重新定义了“序列”的概念(Grbovic and Cheng, 2018),采用基于会话的序列构建策略
面向业务的序列构建
- 会话切分机制:不再把用户所有历史点击简单串联,而是按点击会话(Click Sessions)构建序列;当相邻点击间隔超过 30 分钟时,视为新的会话,从而更准确刻画用户在单一搜索场景下的连续意图
- 行为权重差异化:不同用户行为的信号强度不同,预订相比普通点击更能反映真实偏好,因此在模型训练中赋予更高权重
全局上下文机制
为了强化模型对最终转化行为的学习,Airbnb设计了全局上下文机制
在传统的Skip-Gram模型中,只有在滑动窗口内的物品才被视为上下文,但这种局部窗口无法充分利用最终预订这一强烈的正向信号
Airbnb让用户最终预订的房源(booked listing)与序列中的每一个浏览房源都形成正样本对进行训练,无论它们在序列中的距离有多远
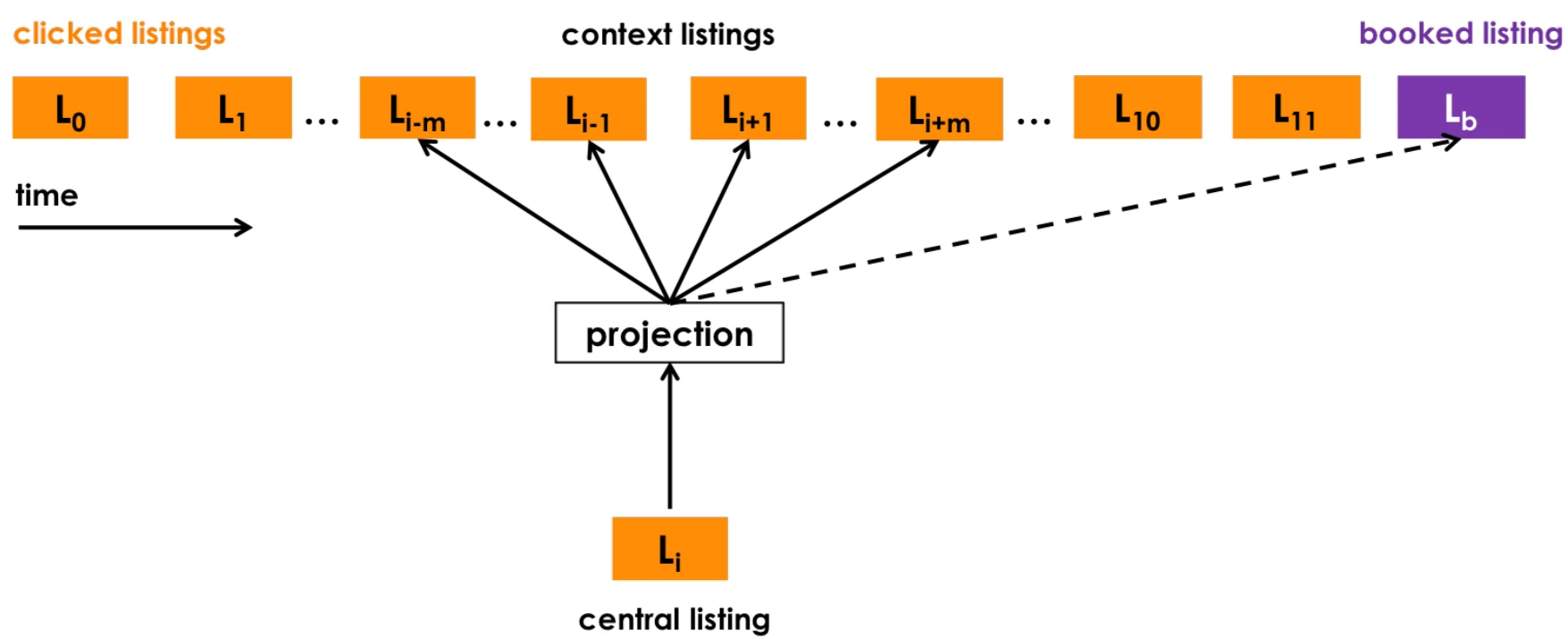
针对有预订行为的会话(booked sessions),Airbnb修改了优化目标函数,增加了全局上下文项:
$$
\color{red}\underset{\theta}{\text{argmax}} \sum_{(l,c) \in \mathcal D_p} \log \frac{1}{1 + e^{-v_c^T v_l}} + \sum_{(l,c) \in \mathcal D_n} \log \frac{1}{1 + e^{v_c^T v_l}} + \log \frac{1}{1 + e^{-v_{l_b}^T v_l}}
$$
前两项是标准的Skip-Gram目标函数:
第一项最大化正样本对$(l,c)$的相似度,其中$l$是目标房源,$c$是滑动窗口内的上下文房源;
第二项最小化负样本对的相似度
关键的创新在于第三项,$l_b$表示用户在该会话中最终预订的房源,预订房源为序列中的每个房源都提供了额外的学习信号
市场感知的负采样
传统负采样通常从全量房源中随机选择负样本,但在 Airbnb 场景下,用户的预订行为高度受地理位置约束,跨市场的负样本过于“容易区分”,会导致模型过度依赖地理特征而忽略房源本身差异
Airbnb 引入了同市场负采样:在负样本中加入与正样本处于同一城市或地区的房源,迫使模型在相同市场内学习更细粒度的房源差异,从而提升推荐精度,对应的损失项为:
$$
\sum_{(l, l_m^-) \in \mathcal D_m} \log \frac{1}{1 + e^{v_{l_m^-}^T v_l}}
$$
其中$l_m^-$表示来自相同市场的负样本
U2I召回
U2I 召回的核心目标是在海量物品中,高效找到与用户兴趣匹配的候选集
其演进过程,本质上是将复杂的用户–物品匹配问题,转化为高效的向量搜索问题
这一转变的关键突破来自于一个统一的架构思想:双塔模型(Two-Tower Model)
无论是经典的因子分解机FM、深度结构化语义模型DSSM,还是YouTube的深度神经网络YouTubeDNN,虽然结构不同,但本质一致:分别将用户和物品编码为向量,通过向量相似度衡量匹配程度
双塔模型
双塔模型将推荐问题拆解为两个相对独立的子问题:
- 用户塔(User Tower):专注于理解用户——处理用户的历史行为、人口统计学特征、上下文信息等,最终输出一个代表用户兴趣的向量$u$
- 物品塔(Item Tower):专注于刻画物品——整合物品的ID、类别、属性、内容特征等,输出一个表征物品特性的向量$v$
在训练完成后,所有物品的向量都可以离线预计算并存储在高效的向量检索系统中(如Faiss、Annoy等)
当用户发起推荐请求时,系统只需实时计算用户向量,然后通过近似最近邻(ANN)搜索获取相似物品
该架构将匹配复杂度从全量匹配$O(U \times I)$转化为向量计算$$O(U + I)$$与近邻搜索
用户与物品的匹配度通常通过点积或余弦相似度计算
$$
score(u, v) = u \cdot v = \sum_{i=1}^{d} u_i v_i
$$
其中$d$是向量维度, 向量空间中的距离反映了用户兴趣与物品特性的匹配程度
FM因子分解机
尽管因子分解机(Factorization Machine, FM) (Rendle, 2010) 提出于深度学习之前,但在思想上可视为双塔模型的早期雏形
FM 的核心思想是:将高维稀疏特征之间的二阶交互,分解为低维向量的内积,从而高效建模用户–物品关系
FM 的预测函数为:
$$
\color{red}\hat y(\mathbf x):=w_{0}+\sum_{i=1}^{n} w_{i} x_{i}+\sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf v_{i}, \mathbf v_{j}\right\rangle x_{i} x_{j}
$$
- $\mathbf x$:用户特征 + 物品特征拼在一起的一个大特征向量
- $x_i$:第 $i$ 个特征的取值,常见0/1
- $w_i$:第 $i$ 个特征的一阶权重,表示每个特征对结果的线性影响
- $\mathbf v_i$:第 $i$ 个特征对应的 $k$ 维隐向量
两个隐向量的内积刻画特征之间的交互强度,只有当两个特征同时出现(都不为 0)时,交互才生效
$$
\left\langle\mathbf v_{i}, \mathbf v_{j}\right\rangle=\sum_{f=1}^{k} v_{i, f} v_{j, f}
$$
原本二阶交互项的计算复杂度为$O(kn^2)$复杂度的二阶交互项,可以通过代数运算重写为(一维的平方展开)
$$
\sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf v_{i}, \mathbf v_{j}\right\rangle x_{i} x_{j} =\sum_{f=1}^{k} \sum_{i=1}^{n} \sum_{j=i+1}^{n} v_{i, f} v_{j, f} x_{i} x_{j}=\sum_{f=1}^{k} \sum_{i<j} v_{i, f} v_{j, f} x_{i} x_{j}=\frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{i=1}^{n} v_{i, f} x_{i}\right)^{2}-\sum_{i=1}^{n} v_{i, f}^{2} x_{i}^{2}\right)
$$
先把所有特征在这个维度上的值加起来,用平方一次性生成所有特征对的交互,减掉不该要的“自己 × 自己”,剩下的就是交互项
该变换将计算复杂度降为$O(kn)$,使 FM 能够高效处理大规模稀疏特征
分解为双塔结构
在召回场景中,同一个用户需要与大量候选物品进行匹配,而用户侧特征在这一过程中是固定不变的
从 FM 的二阶交互形式可以看到,其本质包含三类关系:
| 交互类型 | 是否随用户变 | 是否随物品变 | 在召回中地位 |
|---|---|---|---|
| 用户 × 用户 | ❌ | ❌ | 常数,直接忽略 |
| 物品 × 物品 | ❌ | ✅ | 物品偏置,可离线 |
| 用户 × 物品 | ✅ | ✅ | 核心匹配信号 |
将特征集合划分为用户侧特征集和物品侧特征集后,将FM重新组织,只保留对排序有影响的部分(去除用户×用户项)
$$
score_{FM} = \sum_{t \in I} w_{t} x_{t} + \frac{1}{2} \sum_{f=1}^{k}\left(\left(\sum_{t \in I} v_{t, f} x_{t}\right)^{2} - \sum_{t \in I} v_{t, f}^{2} x_{t}^{2}\right) + \sum_{f=1}^{k}\left( {\sum_{u \in U} v_{u, f} x_{u}}{\sum_{t \in I} v_{t, f} x_{t}} \right)
$$
物品一阶项 + 物品内部二阶交互项 + 用户物品交互项
可以将整个匹配分数重新组织为两个向量的内积形式
$$
\color{red}score_{FM} = V_{item} \cdot V_{user}^T
$$
通过这种重新组织,得到了FM的双塔表示
- 用户向量:$V_{user} = [1; \sum_{u \in U} v_{u} x_{u}]$
- 物品向量:$V_{item} = [\sum_{t \in I} w_{t} x_{t} + \frac{1}{2} \sum_{f=1}^{k}((\sum_{t \in I} v_{t, f} x_{t})^{2} - \sum_{t \in I} v_{t, f}^{2} x_{t}^{2}); \sum_{t \in I} v_{t} x_{t}]$
用户向量包含一个常数项1和用户特征的聚合表示;
物品向量则包含物品的内部交互信息和物品特征的聚合表示,可离线计算;
这样的分解揭示了一个重要原理:即使是复杂的特征交互模式,也可以通过合适的向量表示和简单的内积运算来实现
核心代码
FM召回的双塔实现关键在于如何将数学推导转化为实际的向量表示
用户塔构建了包含常数项和特征聚合的向量:
1 | def build_user_tower(): |
SumPooling通常表示在“特征维度”上聚合,但保留 embedding 维度
物品塔则更为复杂,需要计算一阶线性项和FM交互项:
1 | def build_item_tower(): |
SumScalarLayer通常表示结束 embedding维度,回到标量打分空间
最终通过内积计算匹配分数
1 | fm_score = Dot(axes=1)([item_vector, user_vector]) # [batch_size, 1] |
这种设计使得物品向量可以离线预计算,用户向量实时计算,从而支持高效的召回检索
训练和评估
1 | from funrec import run_experiment |
数据集ml-1m_recall_pos_neg_data(MovieLens 1M)
标签:label(1/0)[负采样]
用户侧:user_id, age, occupation, zip
物品侧:movie_id, genres
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
DSSM
虽然 FM 通过向量分解高效建模特征交互,但其本质仍是线性模型,对复杂的非线性用户–物品关系表达能力有限
深度结构化语义模型(Deep Structured Semantic Model, DSSM) (Huang et al., 2013) 引入深度神经网络分别对用户和物品进行建模,以非线性变换替代线性映射,显著增强了双塔模型的特征表达与表示学习能力
其核心思想是通过深度神经网络将用户和物品映射到共同的语义空间中,通过向量间的相似度计算来衡量匹配程度
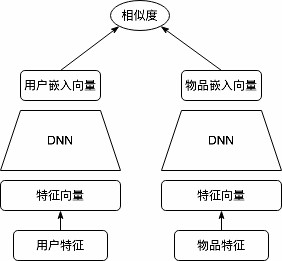
DSSM 采用双塔结构,用户塔与物品塔分别由独立的 DNN 构成
与 FM 的线性建模不同,DSSM 在塔内引入非线性变换以增强特征表达,而用户与物品之间仅在最终通过向量内积进行交互
多分类训练范式
DSSM将召回任务视为一个极端多分类问题,将物料库中的所有物品看作不同的类别
模型的目标是最大化用户对正样本物品的预测概率:
$$
P(y|x,\theta) = \frac{e^{s(x,y)}}{\sum_{j\in M}e^{s(x,y_j)}}
$$
- $s(x,y)$:用户$x$和物品$y$的相似度分数
- $P(y|x,\theta)$:匹配概率
- $M$:整个物料库
由于物料库规模庞大,直接计算这个softmax在计算上不可行,因此实际训练时采用负采样技术,为每个正样本采样一定数量的负样本来近似计算
双塔模型的细节
(Yi et al., 2019)等对双塔结构的细节进行了分析
Yi X, Yang J, Hong L, et al. Sampling-bias-corrected neural modeling for large corpus item recommendations[C]//Proceedings of the 13th ACM conference on recommender systems. 2019: 269-277.
向量归一化:对用户塔和物品塔输出的Embedding进行L2归一化
$$
u \leftarrow \frac{u}{||u||_2}, \quad v \leftarrow \frac{v}{||v||_2}
$$
归一化的主要作用在于解决向量点积不具备度量性质的问题
原始点积既不满足三角不等式,也无法作为稳定的距离度量,可能导致相似性排序与几何直觉不一致
对于三个点$A=(10,0)$、$B=(0,10)$、$C=(11,0)$,使用点积计算会得到$\text{dist}(A,B) < \text{dist}(A,C)$,但这与直观的几何距离不符
在向量归一化后,点积与欧式距离之间建立了等价关系:
$$
||u - v|| = \sqrt{2-2\langle u,v \rangle}
$$
对单位向量而言,最大化点积等价于最小化欧式距离
这种转换的关键意义在于训练与检索的一致性:
模型训练阶段使用归一化后的点积作为相似度目标,而线上 ANN 检索系统通常基于欧式距离进行近邻搜索。二者在数学上等价,从而保证了离线训练学到的向量关系能够在线上检索阶段被正确保留,避免训练–服务不一致问题
温度系数调节
在归一化后的向量计算内积后,除以温度系数$\tau$:
$$
s(u,v) = \frac{\langle u,v \rangle}{\tau}
$$
这里的温度系数$\tau$看起来是个简单的除法操作,但实际上它对模型的训练效果有着深远的影响
从数学角度来看,温度系数本质上是在缩放logits,进而改变Softmax函数的输出分布形状
$\tau < 1$相似度的差异会被放大,这意味着模型会对高分样本给出更高的概率,预测变得更加“确定”
相反$\tau > 1$分布会变得更加平滑,模型的预测也更加保守
核心代码
DSSM的实现核心在于构建独立的用户塔和物品塔,每个塔都是一个深度神经网络:
1 | # 拼接用户侧和物品侧特征 |
关键的向量归一化和相似度计算:
1 | # L2归一化:确保训练与检索的一致性 |
这种设计使得用户和物品的表示完全独立,支持离线预计算物品向量并存储在ANN索引中,实现毫秒级的召回响应
1 | run_experiment('dssm') |
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
YouTubeDNN
YouTube深度神经网络推荐系统 (Covington et al., 2016) 代表了双塔模型演进的一个重要里程碑
YouTubeDNN在架构上延续了双塔设计,但引入了一个关键的思想转变:将召回任务重新定义为“预测用户下一个会观看的视频”
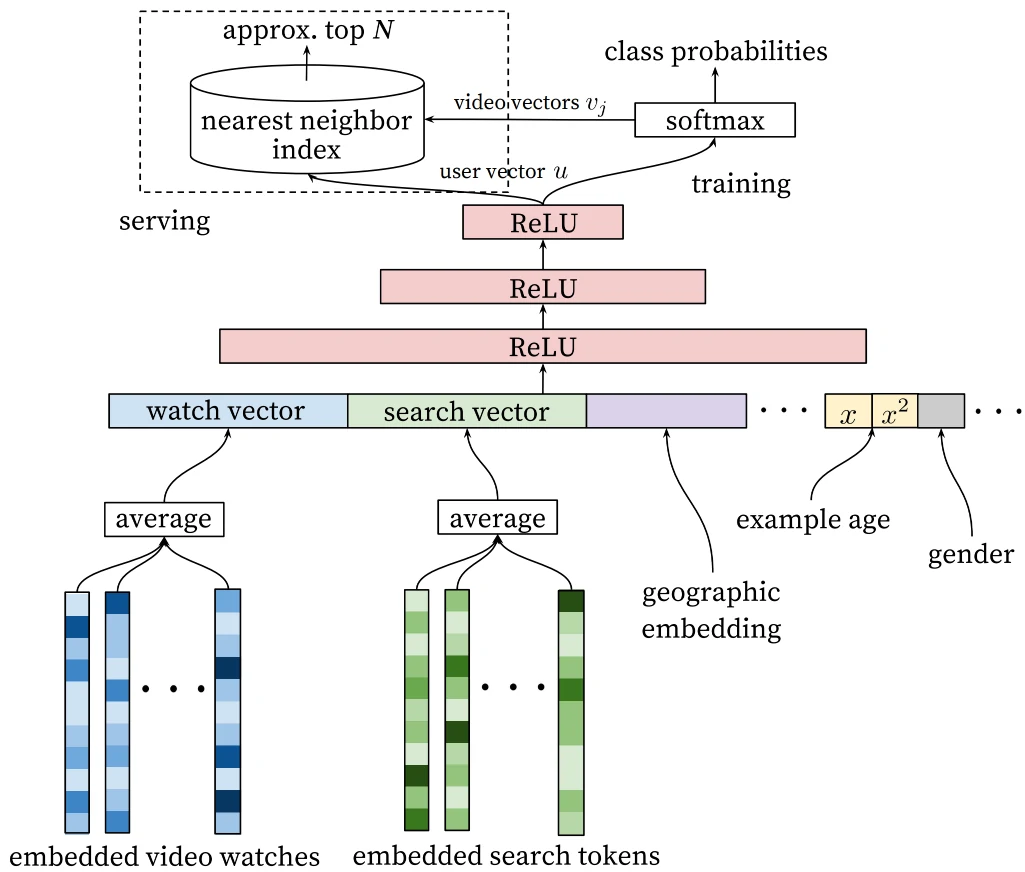
YouTubeDNN 采用了一种非对称双塔结构
用户塔融合了观看历史、搜索行为和人口统计等多源特征,其中历史观看视频的 ID 经嵌入层映射后通过平均池化进行聚合,并引入时间相关因素(Example Age)以建模内容新鲜度的影响
本质是把“用户最近看过的一堆视频”压缩成一个兴趣向量
物品塔结构较为简单,本质上是一个大规模可学习的嵌入矩阵,每个视频对应一个向量,从而避免了复杂的物品特征工程
YouTube 视频数量极大,召回阶段追求速度 + 覆盖,典型的“重用户、轻物品”设计
该模型将“预测用户下一次观看的视频”建模为一个极端多分类问题,形式上类似于 NLP 中的 next-token 预测:
$$
P(w_t=i|U,C) = \frac{e^{v_i \cdot u}}{\sum_{j \in V} e^{v_j \cdot u}}
$$
这里$w_t$表示用户在时间$t$观看的视频,$U$是用户特征,$C$是上下文信息,$V$是整个视频库
由于视频库规模庞大,直接计算全量 Softmax 代价过高,训练阶段采用 Sampled Softmax (1 个正样本 + K 个负样本)进行近似与加速
关键的工程技巧
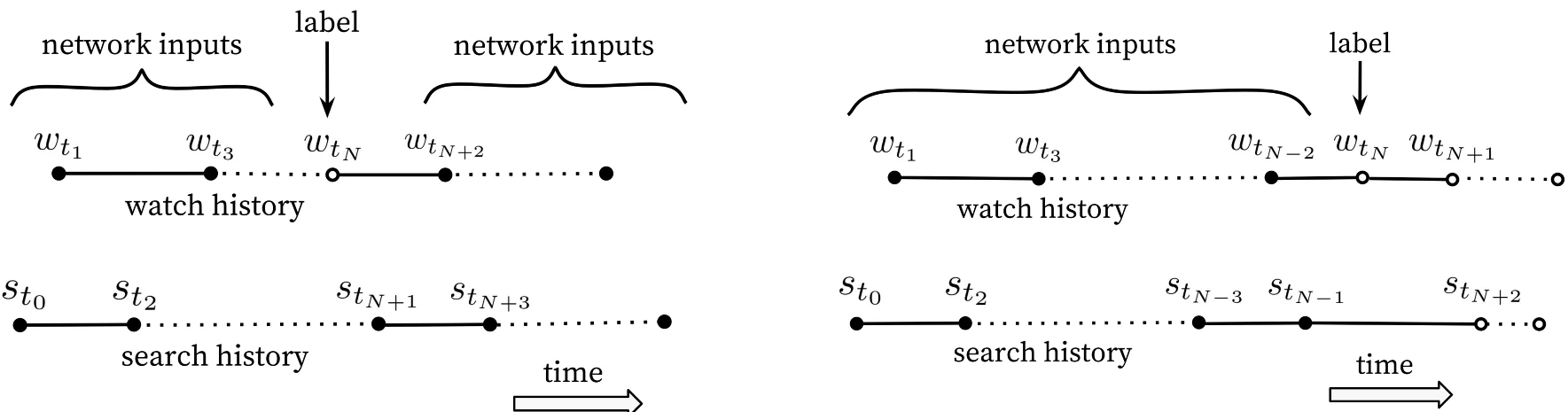
非对称的时序分割:不同于随机划分验证集的做法,YouTubeDNN 采用严格的时序分割策略
对每个预测目标,仅使用其发生之前的用户行为作为输入特征,从而避免未来信息泄露(类似Attention Mask)
基于时间回滚的样本构造方式更符合真实的推荐场景,也更贴合视频消费中存在的顺序性与不对称性
虽然这里考虑了历史,但YouTubeDNN不属于序列召回,是因为在考虑历史特征时只是简单的pooling
负采样策略:为了高效处理数百万类别的Softmax,模型采用重要性采样技术,每次只对数千个负样本进行计算,将训练速度提升并保持有效的区分能力
用户样本均衡:为每个用户生成固定数量的训练样本,防止高活跃用户在训练中占据主导,从而提升对中低活跃用户与长尾兴趣的建模效果
YouTubeDNN 的核心价值在于其工程化的系统设计:训练阶段使用复杂的多分类目标和丰富的用户特征,服务阶段通过离线预计算物品向量、在线生成用户向量,并结合高效的 ANN 检索完成召回,在训练复杂度与线上效率之间取得了良好平衡
这一范式至今仍是大规模召回系统的重要参考
核心代码
YouTubeDNN的用户塔设计体现了“非对称”的思想,它整合了多种用户特征和历史行为序列:
1 | # 整合用户特征和历史行为序列 |
这里不用BN是避免引入batch依赖,对 embedding 表示稳定性不友好
物品塔则采用简化设计,直接使用物品Embedding表:
1 | # 物品Embedding表(从特征列配置中获取) |
训练时采用Sampled Softmax优化,将百万级的多分类问题转化为高效的采样学习
1 | # 构建采样softmax层 |
这种设计的核心优势在于:用户塔可以根据业务需求灵活扩展特征和模型复杂度,而物品塔保持简洁高效,易于离线预计算和实时检索
训练和评估
1 | run_experiment('youtubednn') |
数据集ml-1m_recall_data
特征包括user_id/age/occupation/zip/movie_id/hist_movie_id,max_seq_len=50
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
总结
向量召回的核心贡献在于将推荐系统从“匹配计算”转变为“向量搜索”,通过将用户与物品映射到同一向量空间,把推荐问题统一为相似度搜索问题,从全量匹配优化为高效近邻检索,实现了从$O(U \times I)$到$O(U + I)$的复杂度优化
I2I召回的演进脉络:I2I 召回源于 NLP 领域的 Word2Vec,并沿着“序列语义深化”的方向持续演进
- Item2Vec 将词序列建模思想迁移到用户行为序列,验证了序列共现在推荐中的有效性
- EGES 通过引入商品关系图与辅助属性,缓解了数据稀疏与冷启动问题
- Airbnb 则进一步将业务目标融入序列构建与负采样策略,实现了从相似性优化向转化目标优化的转变
| 模型 | 核心思想 | 关键特点 | 主要价值 |
|---|---|---|---|
| Word2Vec | 通过上下文共现学习向量 | Skip-gram / CBOW 局部上下文预测 |
“向量表示+相似度搜索”方法论起点 |
| Item2Vec | 用户行为序列 ≈ 词序列 | 仅建模物品共现关系 不依赖用户特征 |
验证序列建模在推荐中的可行性 |
| EGES | 图结构 + 多源信息融合 | 引入商品关系图与属性 embedding 缓解稀疏与冷启动 |
提升长尾与冷启动物品表示质量 |
| Airbnb I2I | 业务目标驱动的序列建模 | 会话切分 上下文感知 市场感知负采样 |
从“相似性召回”走向“转化目标召回” |
U2I召回的技术路径:U2I 召回以双塔模型为核心架构,体现了可分解的系统设计思想
- FM 通过向量分解形式刻画用户–物品交互,为双塔结构提供了理论基础
- DSSM 引入深度网络提升了表示能力,并确立了大规模多分类训练与工程化部署范式
- YouTubeDNN 则通过 next-item 预测任务重构训练目标,并结合时序分割与采样优化,使双塔模型在超大规模推荐场景中具备可行性
| 模型 | 核心思想 | 关键特点 | 主要价值 |
|---|---|---|---|
| 双塔模型 | 映射到同一向量空间 | 用户塔 + 物品塔可分解 向量检索 |
高效候选生成,实时配合ANN |
| FM | 用户–物品交互的向量分解 | 显式建模二阶特征交互 线性结构 |
奠定双塔模型的数学基础 |
| DSSM | 深度双塔相似度学习 | DNN 替代线性映射 多分类 / softmax 训练 |
建立工业级双塔训练与部署范式 |
| YouTubeDNN | next-item 预测 | 非对称双塔 时序分割 用户样本均衡 |
证明双塔模型可在超大规模场景落地 |
序列召回
协同过滤和向量召回将用户的历史行为汇总成一个静态表示(比如一个向量),然后基于这个表示进行推荐
但是用户的行为其实是有时间顺序的,而且这个顺序往往包含了重要的信息,如果只是简单地把这些行为加起来或者平均,就丢失了这种时间顺序的信息
序列召回的核心思想在于显式利用用户行为的时间顺序进行建模,相较于静态表示方法,序列召回能够更准确、全面地理解用户兴趣
两类具有代表性的方法:
- 多兴趣用户表示方法:通过多个向量或动态结构来更好地刻画用户的复杂兴趣模式,如 MIND 和 SDM
- 生成式序列预测方法:将推荐问题视为序列建模任务,借鉴 NLP 领域的经验,引入 Transformer 等结构来建模序列依赖关系,如 SASRec 及其后续模型 HSTU 和 TIGER
深化用户兴趣表示
传统的向量召回方法(如双塔模型)通常将用户的历史行为压缩为一个单一的静态向量
这种“平均化”的表示方式虽然计算高效,但难以刻画用户兴趣的复杂性
- 无法表达用户同时存在的多样化兴趣
- 忽略了兴趣的时间特性,难以区分长期稳定的偏好与短期即时需求,例如对摄影的长期关注与临时搜索感冒药所反映的意图差异
MIND
MIND(Multi-Interest Network with Dynamic Routing)(Li et al., 2019)借鉴了胶囊网络中的动态路由机制,将用户历史行为自动聚类为若干兴趣组,并为每一组生成对应的兴趣向量
这些向量分别代表用户在不同兴趣维度上的偏好,使推荐系统能够根据当前场景更有针对性地匹配物品,从而提升对多样化和动态兴趣的建模能力
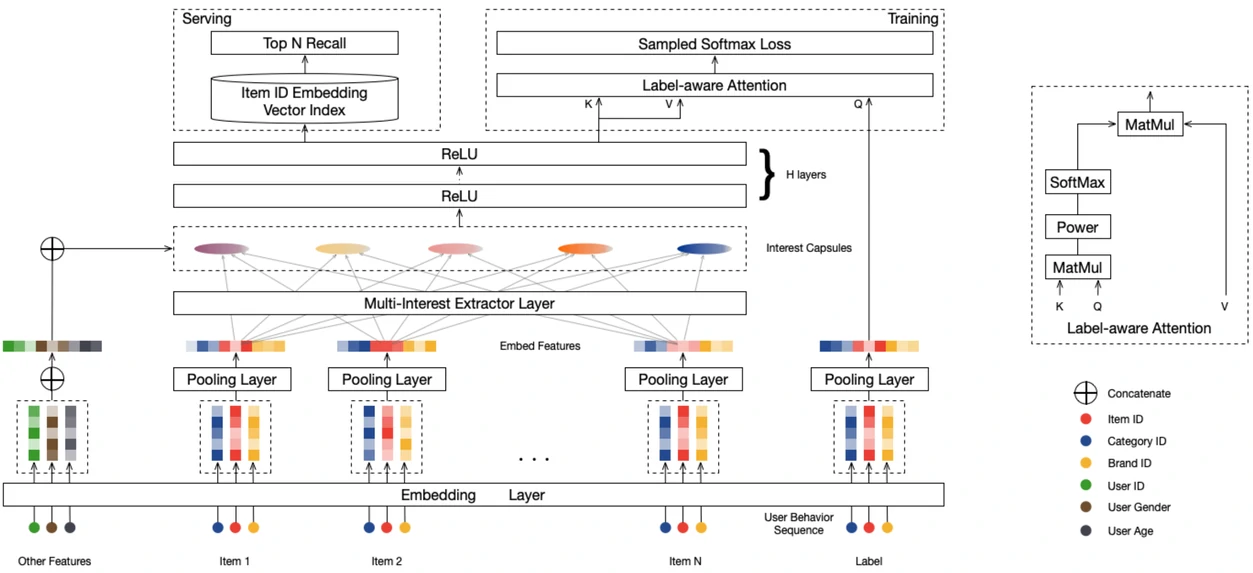
从整体架构来看,除了常规的Embedding层,MIND模型还包含了两个重要的组件:多兴趣提取层和Label-Aware注意力层
多兴趣提取
胶囊网络(Sabour et al., 2017)最初提出于计算机视觉领域,其核心思想是用向量而非标量表示特征,其中向量的方向编码属性信息,长度表示该特征存在的概率。动态路由算法用于确定不同层级胶囊之间的连接强度,通过迭代更新实现对输入特征的软聚类
这种软聚类机制无需预先定义类别数量或明确的边界,而是由数据本身驱动分组过程,正好契合了用户兴趣发现的需求
MIND 模型将胶囊网络的思想引入推荐系统,提出了行为到兴趣(Behavior to Interest,B2I)的动态路由机制:将用户历史行为建模为行为胶囊,将用户的多重兴趣建模为兴趣胶囊,并通过动态路由将相关行为自动聚合到对应的兴趣表示中
针对推荐场景的特点,MIND 对原始动态路由算法进行了若干关键改进:
共享变换矩阵:与原始胶囊网络为每对胶囊使用独立变换矩阵不同,MIND采用共享的双线性映射矩阵$S \in \mathbb R^{d \times d}$
1
2
3
4self.bilinear_mapping_matrix = self.add_weight(
shape=[self.input_units, self.out_units],
initializer=tf.keras.initializers.RandomNormal(stddev=self.init_std),
name="S", dtype=tf.float32)MIND训练的就是$S$矩阵
$S$ 是把“物品行为空间”映射到“兴趣聚合空间”的全局线性规则
这种设计有两个重要考虑
- 用户行为序列长度变化很大,从几十到几百不等,共享矩阵确保了算法的通用性
- 共享变换保证所有兴趣向量位于同一表示空间,便于后续的相似度计算和检索操作
行为与兴趣之间的路由连接强度定义为:
$$
b_{ij} = \boldsymbol u_j^T \boldsymbol S \boldsymbol e_i
$$
其中 $\boldsymbol e_i$ 表示用户历史行为 $i$ 的物品向量,$\boldsymbol u_j$ 表示第 $j$ 个兴趣胶囊的向量,$b_{ij}$ 衡量行为 $i$ 与兴趣 $j$ 的关联程度随机初始化策略:为避免所有兴趣胶囊收敛到相同状态,算法采用高斯分布随机初始化路由系数 $b_{ij}$
这一策略类似于K-Means聚类中的随机中心初始化,确保不同兴趣胶囊能够捕捉用户兴趣的不同方面
1
2
3
4
5
6self.routing_logits = self.add_weight(
shape=[1, self.k_max, self.max_len], # batch维为1,因为对所有用户都一样
initializer=tf.keras.initializers.RandomNormal(stddev=self.init_std), # 不一定0初始化
trainable=False, name="B", dtype=tf.float32)
# routing_logits(b_ij)不参与梯度下降
# S 参与训练,在下一次前向传播计算中,b_ij会被重新计算成不一样的结果如果$b_{ij}$进入训练,结果会变成记忆行为序列中哪个位置的行为匹配哪个兴趣,和具体的行为内容无关了
自适应兴趣数量:考虑到不同用户的兴趣复杂度差异很大,MIND引入了动态兴趣数量机制
$$
K_u’ = \max(1, \min(K, \log_2 (|\mathcal I_u|)))
$$
其中 $|\mathcal I_u|$ 表示用户 $u$ 的历史行为数量,$K$ 是预设的最大兴趣数这种设计为行为较少的用户节省计算资源,同时为活跃用户提供更丰富的兴趣表示
改进后的动态路由过程通过迭代方式进行更新,在每轮迭代中更新路由系数 $b_{ij}$ 和兴趣胶囊向量 $\boldsymbol u_j$,直到收敛
关键的兴趣胶囊向量$\boldsymbol u_j$通过以下步骤计算:
计算路由权重:对于每一个历史行为(低层胶囊$i$),其分配到各个兴趣(高层胶囊 $j$)的权重 $w_{ij}$ 通过对路由系数 $b_{ij}$ 进行Softmax操作得到
$$
w_{ij} = \frac{\exp{b_{ij}}}{\sum_{k=1}^{K_u’} \exp{b_{ik}}}
$$
这里的 $w_{ij}$ 表示行为 $i$ 属于兴趣 $j$ 的“软分配”概率聚合行为以形成兴趣向量:每一个兴趣胶囊的初步向量$\boldsymbol z_j$是通过对所有行为向量$\boldsymbol e_i$进行加权求和得到的,每个行为向量在求和前会先经过共享变换矩阵$\boldsymbol S$的转换
$$
\boldsymbol z_j = \sum_{i\in \mathcal I_u} w_{ij} \boldsymbol S \boldsymbol e_i
$$
该过程本质上实现了对用户行为的软聚类,将相关行为聚合为代表特定兴趣的向量1
behavior_embddings = [B, max_len, d] # 用户按时间排序的一串历史行为 embedding
1
2
3
4# 2. 通过共享的双线性映射矩阵 S 把所有行为投影到兴趣空间
behavior_embdding_mapping = tf.tensordot(
behavior_embddings, self.bilinear_mapping_matrix, axes=1
) # [B, max_len, out_units] 对应Se_i不同的行为序列映射到兴趣空间的结果不一样,也就是从行为序列中建模用户状态
非线性压缩:在完成行为聚合后,模型通过非线性的squash函数对中间向量$\boldsymbol z_j$进行压缩,得到本轮迭代的最终兴趣胶囊向量$\boldsymbol u_j$
squash函数在不改变向量方向的前提下,将其模长约束到$[0, 1)$区间内,使向量长度可解释为兴趣存在的强度,而方向编码具体的兴趣语义
$$
\boldsymbol u_j = \text{squash}(\boldsymbol z_j) = \frac{\left\lVert \boldsymbol z_j \right\rVert ^ 2}{1 + \left\lVert \boldsymbol z_j \right\rVert ^ 2} \frac{\boldsymbol z_j}{\left\lVert \boldsymbol z_j \right\rVert}
$$更新路由系数(Updating Routing Logits):最后根据新生成的兴趣胶囊$\boldsymbol u_j$和行为向量$\boldsymbol e_i$的一致性(通过点积衡量),来更新下一轮迭代的路由系数
$$
b_{ij} \leftarrow b_{ij} + \boldsymbol u_j^T \boldsymbol S \boldsymbol e_i
$$
以上四个步骤会重复进行固定的次数(通常为3次),最终输出收敛后的兴趣胶囊向量集合${\boldsymbol u_j, j=1,…,K_{u}^\prime}$作为该用户的多兴趣表示
| 变量 | 物理意义 |
|---|---|
| $(e_i)$ | 原始行为的物品向量 |
| $(S e_i)$ | 行为在兴趣空间的投影 |
| $(u_j)$ | 当前估计的兴趣向量 |
| ($u_j^T S e_i$) | 行为与兴趣的一致性 |
| ($b_{ij}$) | 到目前为止,这种一致性累计了多少 |
| ($w_{ij}$) | 当前轮的分配概率 |
| 变量 | 是否可训练 | 生命周期 | 物理意义 |
|---|---|---|---|
| $S$ | ✅ | 跨 step / epoch | 行为→兴趣的判定规则 |
| $b_{ij}$ | ❌ | 一次 forward | 行为→兴趣的累计倾向 |
| $u_j$ | ❌ | 一次 forward | 当前用户的兴趣表示 |
核心代码
MIND的核心在于胶囊网络的动态路由实现
在每次迭代中,模型首先通过softmax计算路由权重,然后通过双线性变换聚合行为向量,最后使用squash函数进行非线性压缩
1 | capsule_mask[b, j, i] = |
假设
1 | k_max = 4 # 最大兴趣数 |
有效区域
1 | 兴趣 0 [✔ ✔ ✔ ✘ ✘] |
1 | # 动态路由的核心循环 |
这里的squash函数实现了向量长度的非线性压缩,确保输出向量的模长在$[0, 1)$区间内:
1 | def squash(inputs): |
标签感知的注意力机制
多兴趣提取层会为用户生成多个兴趣向量${u_1,u_2,\cdots,u_K }$,刻画用户在不同行为模式下的潜在兴趣
在训练阶段需要确定哪个兴趣向量与当前目标商品最相关
由于训练时已知用户真实点击的下一个商品,MIND 利用该标签信息,引入标签感知注意力(Label-aware Attention),指导模型在多个兴趣向量中选择最匹配的一项
标签感知注意力以目标商品向量作为查询(Query),以用户的多个兴趣向量作为键和值(Key/Value),计算过程为
$$
v_u = V_u \cdot \text{Softmax}(\text{pow}(V_u^T e_i, p))
$$
其中
$V_u = (u_1, \ldots, u_K)$表示用户的兴趣胶囊矩阵
$e_i$是目标商品 $i$ 的embedding向量
$p$是控制注意力集中度的超参数,决定注意力的“软硬”程度
$p\rightarrow 0$:各兴趣向量权重接近均匀;
$p$ 增大:注意力逐渐集中到与目标商品最相似的兴趣
$p\rightarrow \infty$:退化为硬选择,只保留相似度最高的兴趣向量
实验表明,使用较大的 $p$ 值能够加快模型收敛速度
标签感知注意力直接在由共享映射矩阵$S$和动态路由共同确定的兴趣空间中,利用目标商品embedding和多兴趣表示${ u_j}$进行匹配和选择,通过标签感知得到当前训练样本对应的用户向量$v_u$
MIND模型的训练目标是:最大化$v_u$与正样本商品的相似度,同时最小化与负样本的相似度
由于商品规模巨大,MIND 采用与 YouTubeDNN 相同的 Sampled Softmax,通过采样少量负样本近似完整 softmax 计算,从而降低训练成本
核心是使用目标商品向量作为查询,计算与各个兴趣向量的相似度:
1 | def call(self, inputs, training=None, **kwargs): |
训练和评估
1 | from funrec import run_experiment |
数据集ml-1m_recall_data
用户侧稀疏特征:user_id, age, occupation, zip(group=user_dnn)
目标物品特征:movie_id, genres(group=target_item)
历史序列特征:hist_movie_id, hist_genres(group=raw_hist_seq,会被整理为长度 max_seq_len=50 的序列)
返回:
- user_model:输入用户相关特征,输出多兴趣用户向量
- item_model:输入 movie_id,输出 item embedding
1 | +---------------+--------------+-----------+----------+----------------+---------------+ |
SDM
MIND 通过多兴趣建模有效缓解了用户兴趣过于单一的问题,能够刻画用户在不同主题下的潜在兴趣结构
虽然MIND能捕捉多个兴趣,但并未在结构上显式地区分它们的时效性,对历史行为的建模未引入明确的时间权重
序列深度匹配模型(Sequential Deep Matching,SDM)(Lv et al., 2019) 正是为了解决这一问题而提出的
SDM模型的核心思想是分别建模用户的短期即时兴趣和长期稳定偏好,然后智能地融合它们
.webp)
捕捉短期兴趣
为了精准捕捉短期兴趣,SDM 设计了一套三层结构来处理用户的当前会话序列**(左下角)**
首先,将用户在当前会话中的商品点击序列输入 LSTM 网络,以建模行为之间的时序依赖关系
为什么 SDM 利用 LSTM + Self-Attention,而不是直接用 Transformer?
Transformer更擅长长序列,全局建模以及大规模数据,而对于搜推场景,会话序列其实通常很短,噪声点击很常见
LSTM对随机点击更鲁棒,并且LSTM + Attention参数更少,相比直接使用 Transformer 更适合短会话、高噪声的推荐场景
LSTM 通过遗忘门Forget Gate、输入门Input Gate和输出门Output Gate对信息进行选择性保留与更新,从而在序列建模过程中抑制随机点击等噪声行为,更好地提取与当前意图相关的有效信息
$$
\begin{aligned}
\boldsymbol i \boldsymbol n_{t}^{u} &=\sigma\left(\boldsymbol W_{i n}^{1} \boldsymbol e_{i_{t}^{u}}+\boldsymbol W_{i n}^{2} \boldsymbol h_{t-1}^{u}+b_{i n}\right)
\\
\boldsymbol f_{t}^{u} &=\sigma\left(\boldsymbol W_{f}^{1} \boldsymbol e_{i_{t}^{u}}+\boldsymbol W_{f}^{2} \boldsymbol h_{t-1}^{u}+b_{f}\right) \\
\boldsymbol o_{t}^{u} &=\sigma\left(\boldsymbol W_{o}^{1} \boldsymbol e_{i_{t}^{u}}+\boldsymbol W_{o}^{2} \boldsymbol h_{t-1}^{u}+b_{o}\right) \\
\boldsymbol c_{t}^{u} &=\boldsymbol f_{t}^{u} \boldsymbol c_{t-1}^{u}+\boldsymbol i \boldsymbol n_{t}^{u} \tanh \left(\boldsymbol W_{c}^{1} \boldsymbol e_{i_{t}^{u}}+\boldsymbol W_{c}^{2} \boldsymbol h_{t-1}^{u}+b_{c}\right) \\
\boldsymbol h_{t}^{u} &=\boldsymbol o_{t}^{u} \tanh \left(\boldsymbol c_{t}^{u}\right)
\end{aligned}
$$
- $\boldsymbol e_{i_{t}^{u}}$:第$t$个时间步的商品embedding
- $\sigma$:sigmoid激活函数
- $\boldsymbol W$:权重矩阵,$b$表示偏置向量
每个时间步都输出隐藏状态$\boldsymbol h_{t}^{u} \in \mathbb R^{d \times 1}$,最终得到会话序列的表示
$$
\boldsymbol X^{u} = [\boldsymbol h_{1}^{u}, \ldots, \boldsymbol h_{t}^{u}]
$$
1 | # 1. 序列信息学习层:使用LSTM处理序列依赖 |
在获得序列表示后,SDM 引入多头自注意力机制以刻画短期兴趣的多样性
通过对序列表示$\boldsymbol X^{u}$进行多组线性映射,模型在不同注意力头中并行关注序列的不同兴趣模式,每个注意力头独立计算序列内部的相关性(这里是自注意力),并生成对应的兴趣表示
不需要位置编码是因为LSTM的隐藏状态里已经包含了时序信息
$$
head_{i}^{u}=\operatorname{Attention}\left(\boldsymbol W_{i}^{Q} \boldsymbol X^{u}, \boldsymbol W_{i}^{K} \boldsymbol X^{u}, \boldsymbol W_{i}^{V} \boldsymbol X^{u}\right) = \operatorname{Attention}(Q_i^u,K_i^u,V_i^u)\\
\operatorname{Attention}(Q,K,V) = \operatorname{softmax}(QK^T)V
$$
这里和transformer的注意力机制的区别只在于没有$\sqrt d_k$的分母
因为NLP中的embedding维度通常512/1024,维度大,容易出现数值爆炸,需要除$\sqrt d_k$防止梯度爆炸;推荐系统的embedding维度通常在32/64/128,点积数值可控
其中$Q_{i}^{u}$、$K_{i}^{u}$、$V_{i}^{u}$分别表示第$i$个头的查询、键、值矩阵,$\boldsymbol W_{i}^{Q}$、$\boldsymbol W_{i}^{K}$、$\boldsymbol W_{i}^{V}$是对应的权重矩阵
所有注意力头的输出经过拼接和线性变换后,得到融合多种兴趣信息的序列表示
$$
\hat X^{u}=\text{MultiHead}\left(X^{u}\right)=W^{O} \operatorname{concat}\left(head_{1}^{u}, \ldots, head_{h}^{u}\right)
$$
$W^{O}$是输出权重矩阵
1 | # 2. 多兴趣提取层:多头自注意力捕捉序列内的复杂关系 |
在此基础上 SDM 进一步引入个性化注意力层,利用用户画像向量$\boldsymbol e_u$作为查询(这里不是自注意力),对多头注意力输出进行加权,从而突出与用户长期偏好更一致的会话行为
$$
\begin{aligned}
\alpha_{k} &=\frac{\exp\left(\hat{\boldsymbol h_{k}^{u T}} \boldsymbol e_{u}\right)}{\sum_{k=1}^{t} \exp\left(\hat{\boldsymbol h_{k}^{u T}} \boldsymbol e_{u}\right)} \\
\boldsymbol s_{t}^{u} &=\sum_{k=1}^{t} \alpha_{k} \hat{\boldsymbol h_{k}^{u}}
\end{aligned}
$$
$\hat{\boldsymbol h_{k}^{u}}$是多头注意力输出$\hat{X}^{u}$中第$k$个位置的隐藏状态,$\alpha_{k}$是对应的注意力权重
通过该机制,模型能够在短期会话兴趣的基础上注入用户的个性化信息,最终得到融合长期偏好与短期意图的短期兴趣表示$\boldsymbol{s}_{t}^{u} \in \mathbb{R}^{d \times 1}$
1 | # 3. 用户个性化注意力层:使用用户画像作为查询向量 |
核心代码
SDM的短期兴趣建模采用了三层架构,逐步从原始序列中提取用户的即时兴趣
1 | # 1. 序列信息学习层:使用LSTM处理序列依赖 |
个性化注意力层的实现通过用户画像与序列特征的点积来计算注意力权重:
1 | class UserAttention(tf.keras.layers.Layer): |
捕捉长期兴趣
长期行为蕴含着稳定而丰富的偏好信息,但这类偏好并不依赖严格的时间顺序,更适合从特征维度进行建模
SDM 不再将长期行为视为单一序列,而是按照不同特征类型对历史行为进行拆分,形成多个特征子集**(左上角)**:
$$
\mathcal L^{u}={\mathcal L_{f}^{u} \mid f \in \mathcal F}
$$
包括:
- 交互过的商品ID集合 $\mathcal{L}^{u}_{id}$
- 叶子类别集合 $\mathcal{L}^{u}_{leaf}$
- 一级类别集合 $\mathcal{L}^{u}_{cate}$
- 访问过的商店集合 $\mathcal{L}^{u}_{shop}$
- 交互过的品牌集合 $\mathcal{L}^{u}_{brand}$
1 | # 从不同特征维度对长期行为进行聚合 |
long_history_features 是一个 dict
1 | { |
这种特征维度的分离使模型能够从不同角度理解用户的长期偏好模式
对每个特征子集,模型使用注意力机制计算用户在该维度上的偏好
将特征实体$f^u_k \in \mathcal L^u_f$通过嵌入矩阵转换为向量$\boldsymbol g^u_k$,然后使用用户画像$\boldsymbol e_u$计算注意力权重
$$
\begin{aligned}
\alpha_{k} &=\frac{\exp (\boldsymbol g_{k}^{u T} \boldsymbol e_{u})}{\sum_{k=1}^{|\mathcal L_{f}^{u}|} \exp (\boldsymbol g_{k}^{u T} \boldsymbol e_{u})} \\
\boldsymbol z_{f}^{u} &=\sum_{k=1}^{|\mathcal L_{f}^{u}|} \alpha_{k} \boldsymbol g_{k}^{u}
\end{aligned}
$$
其中$\left|\mathcal L_{f}^{u}\right|$表示特征子集的大小
最终将各特征维度的表示拼接,通过全连接网络得到长期兴趣表示
$$
\begin{aligned}
\boldsymbol z^{u} &=\operatorname{concat}({\boldsymbol z_{f}^{u} \mid f \in \mathcal F}) \\
\boldsymbol p^{u} &=\tanh (\boldsymbol W^{p} \boldsymbol z^{u}+\boldsymbol b)
\end{aligned}
$$
核心代码
长期兴趣的建模采用特征维度聚合的方式,对每个特征维度分别应用注意力机制
1 | # 从不同特征维度对长期行为进行聚合 |
长短期兴趣融合
用户的长期兴趣包含大量稳定偏好信息,但在具体推荐场景中,只有其中一部分与当前决策相关,简单的拼接或加权求和难以准确提取相关信息
SDM设计了门控融合机制,类似LSTM中的门控思想(中间部分),对长期兴趣和短期兴趣进行自适应融合
门控网络接收三个输入:用户画像$\boldsymbol e_{u}$、短期兴趣$\boldsymbol s_{t}^{u}$和长期兴趣$\boldsymbol p^{u}$,生成门控向量$\boldsymbol G_{t}^{u} \in \mathbb R^{d \times 1}$,取值范围在[0,1]
$$
\boldsymbol G_{t}^{u} = \operatorname{sigmoid}(\boldsymbol W^{1} \boldsymbol e_{u}+\boldsymbol W^{2} \boldsymbol s_{t}^{u}+\boldsymbol W^{3} \boldsymbol p^{u}+\boldsymbol b)
$$
门控向量的每一维表示在对应兴趣维度上,模型更应依赖短期兴趣还是长期偏好
最终的用户表示由门控向量对短期兴趣$\boldsymbol s_{t}^{u}$和长期兴趣$\boldsymbol p^{u}$进行逐维加权获得($\odot$表示逐元素乘法):
$$
\boldsymbol o_{t}^{u} = (1-\boldsymbol G_{t}^{u} ) \odot \boldsymbol p^{u}+\boldsymbol G_{t}^{u} \odot \boldsymbol s_{t}^{u}
$$
通过这种逐维的门控融合方式,模型能够在不同兴趣维度上灵活选择长期或短期信息,既保留用户稳定偏好,又突出当前行为意图,从而避免简单融合策略带来的信息干扰,更准确地刻画用户的真实需求
核心代码
1 | class GatedFusion(tf.keras.layers.Layer): |
整个SDM模型的最终实现将三个模块串联起来:
1 | # 短期兴趣建模 |
生成式召回方法
序列召回方法的核心目标是分析用户的历史行为,并将其总结成一个或多个能够代表用户兴趣的向量,好比是为用户拍摄一张静态的“兴趣快照”,用以在海量物品中进行检索
生成式召回不再总结用户兴趣,而是将推荐问题建模为序列预测任务,直接学习物品之间的动态依赖关系,并预测用户在当前状态下最可能交互的下一个物品
SASRec是生成式召回的代表性起点,它首次将 Transformer 架构引入推荐序列建模,通过自注意力机制对用户行为序列进行建模,并以“预测下一个物品 ID”为目标,验证了该范式在召回任务中的有效性
SASRec后续研究主要沿着两个方向进一步深化这一范式:
- 增强输入的信息:HSTU将用户属性、行为类型、时间等多源异构信息统一建模为连续的“事件流”,为模型提供更加丰富的上下文信息
- 增强物品的信息:传统推荐系统中,物品通常用简单的ID来表示,这种方式虽然直观,但缺乏语义信息。TIGER 摒弃了单一物品 ID 表示方式,引入由多个码本组成的“语义 ID”,使物品表示具备更强的语义表达能力,同时适用于序列输入和预测目标
SASRec
在SASRec出现之前,序列推荐方法主要依赖马尔可夫链和 RNN 等模型,但存在明显缺陷
- 马尔可夫链 (Rendle et al., 2010) 通常只建模最近的少量行为,难以利用完整的历史信息;
- RNN虽然理论上能够捕捉长期依赖关系,但其串行计算方式限制了训练效率和并行能力
SASRec (Kang and McAuley, 2018) 的核心出发点在于:在保留完整行为序列信息的同时,高效地建模其中最关键的依赖关系,引入了在自然语言处理领域已被充分验证的 Transformer 架构(Vaswani et al., 2017)
在 SASRec 中,用户行为序列被视为一段“句子”,序列中的物品对应“词语”,模型通过自注意力机制自动学习序列中任意两个物品之间的关联强度,并基于这些全局依赖关系预测用户下一步可能交互的物品
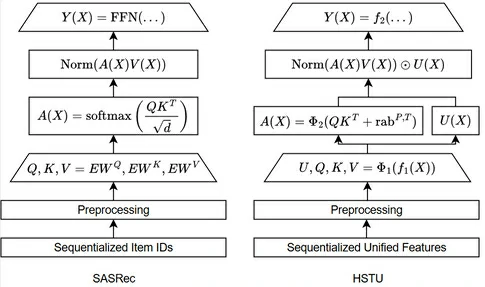
类似于Transformer,SASRec的基本模块如图左所示,主要包含自注意力层和前馈网络层两个组件
自注意力层
对于序列中的每个商品,通过嵌入矩阵 $\bf M\in\mathbb R^{|\mathcal I|\times d}$ 将其映射为d维向量,其中 $|\mathcal I|$ 是商品总数
输入序列的嵌入矩阵记为 $\bf E\in\mathbb R^{n\times d}$,其中 $\bf E_i=\bf M_{s_i}$
由于自注意力机制本身无法感知位置信息,入了可学习的位置Embedding $\bf P\in\mathbb R^{n\times d}$,因此最终的序列输入表示为:
$$
\begin{split}\widehat{\bf E}=\left[
\begin{array}{c}
\bf M_{s_1}+\bf P_{1} \\
\bf M_{s_2}+\bf P_{2} \\
\dots \\
\bf M_{s_n}+\bf P_{n}
\end{array}
\right]\end{split}
$$
SASRec使用自注意力机制来捕捉序列中物品之间的依赖关系,采用了缩放点积注意力:
$$
\text{Attention}(\bf Q,\bf K,\bf V)=\text{Softmax}\left(\frac{\bf Q\bf K^T}{\sqrt{d}}\right)\bf V
$$
$\sqrt{d}$是缩放因子用于稳定训练
这里自注意力机制需要采用因果掩码,不能偷看未来的行为
前馈网络层


 (1).png)