FunRec 推荐系统_精排模型

在完成候选的快速筛选后，精排阶段需要对上千个候选进行更准确的偏好预测，并在可接受的延迟内兼顾效果、泛化性和稳定性

精排模型的发展路径较为清晰，Wide & Deep 将线性模型的记忆能力与深度模型的泛化能力结合，成为常用的基础框架

随着对特征交互的重视，从 FM 到 DeepFM、xDeepFM，再到基于注意力机制的自动交互建模，模型逐步提升了对复杂特征关系的刻画能力

为了刻画用户兴趣的多样性和变化过程，序列建模被引入精排，DIN 关注不同兴趣的匹配，DIEN 建模兴趣的演化，DSIN 进一步利用会话信息，使模型能够更好地理解用户的动态行为

在实际业务中，精排模型往往需要同时优化多个目标，并适配不同场景。通过多目标和多场景建模，结合合理的架构设计和动态权重策略，模型可以在复杂环境中取得更优的整体效果

记忆与泛化

在构建推荐模型时，常常追求两个看似矛盾的目标：记忆(Memorization)与泛化(Generalization)

• 记忆能力：模型能够学习并记住那些在历史数据中频繁共同出现的特征组合。例如，模型记住“买了A的用户，通常也会买B”，这种能力可以精准地捕捉显性、高频的关联，为用户提供与他们历史行为高度相关的推荐
• 泛化能力：模型能学到特征间的深层关系，处理训练时很少见到的特征组合。例如，模型发现“物品A和物品C都是同一类的，用户喜欢这类东西”，那就可以给喜欢A的用户推荐C，哪怕用户以前没见过C，这能让推荐更丰富一些

2016年Google提出Wide & Deep，这个模型的想法很直接：既然需要两种能力，那就设计两个部分，然后让它们一起训练，通过联合训练的方式配合工作

模型的设计思路是把结构分成两块，各自负责不同的事情：

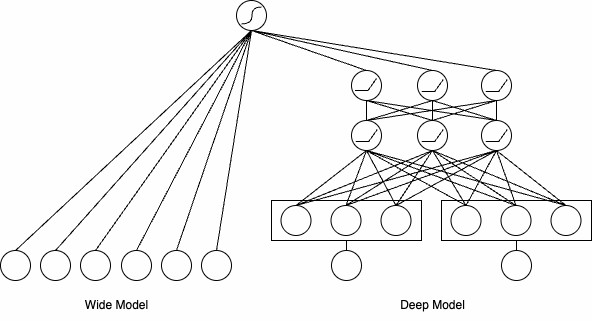
记忆的捷径：Wide部分

Wide部分本质上是一个广义线性模型，比如逻辑回归

它的优势在于结构简单、可解释更强，并且能高效地“记忆”那些显而易见的关联规则。其数学表达形式如下：
$$
y=\mathbf w^T \mathbf x+b
$$
Wide部分的关键在于其输入的特征向量，不仅包含原始特征，更重要的是包含了大量人工设计的交叉特征(Cross-product Features)

交叉特征可以将多个独立的特征组合成一个新的特征，用于捕捉特定的共现模式

核心代码：

为每个特征组合分配一个独立的权重，通过查表操作直接“记住”历史数据中的共现模式

# 遍历所有需要交叉的特征对
for i in range(len(cross_feature_columns)):
    for j in range(i + 1, len(cross_feature_columns)):
        fc_i = cross_feature_columns[i]
        fc_j = cross_feature_columns[j]

        # 获取两个特征的输入
        # feat_i / feat_j 是离散特征的 id
        feat_i = input_layer_dict[fc_i.name]  # [B, 1]
        feat_j = input_layer_dict[fc_j.name]  # [B, 1]

        # 为每个特征对创建独立的权重表
        cross_vocab_size = fc_i.vocab_size * fc_j.vocab_size
        cross_embedding = Embedding(
            input_dim=cross_vocab_size,
            output_dim=1,  # 标量权重，直接记住这对特征的影响
            name=f"cross_{fc_i.name}_{fc_j.name}"
        )

        # 将特征对组合成单一索引并查找权重
        combined_index = feat_i * fc_j.vocab_size + feat_j  # 计算在特征对权重表中的位置
        cross_weight = cross_embedding(combined_index)  # 查表得到这对特征的权重
        cross_weights.append(cross_weight)

# 所有交叉特征权重相加
cross_logits = tf.add_n(cross_weights) # [B, 1]

举例

user_gender        ∈ {0: 女, 1: 男}                vocab_size = 2
user_age_bucket    ∈ {0: 18-24, 1:25-34, 2:35-44}  vocab_size = 3
item_category      ∈ {0: 数码, 1:服饰, 2:食品, 3:家居} vocab_size = 4

cross_feature_columns = [
    user_gender,
    user_age_bucket,
    item_category
]

样本	user_gender	user_age_bucket	item_category
A	男 (1)	25-34 (1)	数码 (0)
B	女 (0)	35-44 (2)	服饰 (1)

input_layer_dict = {
    "user_gender":     [[1], [0]],
    "user_age_bucket": [[1], [2]],
    "item_category":   [[0], [1]]
}

以 user_gender × user_age_bucket 为例

feat_i = user_gender     # [[1], [0]]
feat_j = user_age_bucket # [[1], [2]]

cross_vocab_size = 2 * 3 = 6
cross_embedding = Embedding(input_dim=6, output_dim=1)

计算联合索引

1 * 3 + 1 = 4  → 男 × 25-34
0 * 3 + 2 = 2  → 女 × 35-44
combined_index = [[4], [2]]

需要已经学好的cross_embedding，假设

w2 = -0.3
w4 = +0.8
cross_weight = [[+0.8], [-0.3]]

最终是所有交叉项求和

样本A：
gender × age        : +0.8
gender × category   : +1.2
age × category      : +0.6
--------------------------------
cross_logits(A)     = +2.6

样本B：
gender × age        : -0.3
gender × category   : +0.4
age × category      : -0.2
--------------------------------
cross_logits(B)     = -0.1

学习复杂关系：Deep部分

Deep 部分是一个标准的前馈神经网络(DNN)，主要负责模型的泛化能力

相比依赖人工特征交叉的 Wide 部分，Deep 部分能够自动学习特征之间的高阶、非线性关系

工作流程如下：将高维稀疏的类别特征(如用户 ID、物品 ID)先通过嵌入层映射为低维稠密向量，再将这些向量输入 DNN 进行建模。嵌入向量能够表达特征的潜在语义，是模型实现泛化的关键

例如，《流浪地球》和《三体》的电影ID在嵌入空间中的距离，可能会比《流浪地球》和《熊出没》更近

随后，这些嵌入向量与其他数值特征拼接在一起，被送入多层神经网络中进行前向传播：
$$
a^{(l+1)}=f(W^{(l)}a^{(l)}+b^{(l)})
$$
其中，$a^{(l)}$是第$l$层的激活值，$W^{(l)}$和$b^{(l)}$是该层的权重和偏置，$f$是激活函数(如ReLU)

通过逐层抽象，DNN能够发掘出数据中隐藏的复杂模式，从而对未曾见过的特征组合也能做出合理的预测

核心代码：

# 1. 特征嵌入：将稀疏的类别特征转换为稠密向量
group_feature_dict = {}
for group_name, _ in group_embedding_feature_dict.items():
    group_feature_dict[group_name] = concat_group_embedding(
        group_embedding_feature_dict, group_name, axis=1, flatten=True
    )  # 按group_name拼接多个特征向量

# 2. 深度神经网络：逐层学习特征的非线性组合
deep_logits = []
for group_name, group_feature in group_feature_dict.items():
    # 构建多层神经网络
    deep_out = DNNs(
        units=dnn_units,  # 例如 [64, 32]
        activation="relu",  # ReLU激活函数
        dropout_rate=dnn_dropout_rate
    )(group_feature)

    # 输出层：将深度特征映射为预测分数
    deep_logit = tf.keras.layers.Dense(1, activation=None)(deep_out)
    deep_logits.append(deep_logit)

group_embedding_feature_dict是一个按特征组组织 embedding 的字典

group_embedding_feature_dict = {
    "user": {
        "user_id":      user_id_embedding,      # [B, D]
        "user_gender":  gender_embedding,        # [B, D]
        "user_age":     age_embedding            # [B, D]
    },
    "item": {
        "item_id":      item_id_embedding,       # [B, D]
        "item_category":category_embedding       # [B, D]
    }
}

group_feature_dict = {
    "user": Tensor[B, 3*D],
    "item": Tensor[B, 2*D]
}

两者结合

Wide & Deep模型通过联合训练，将两部分的输出结合起来进行最终的预测。其预测概率如下：
$$
P(Y=1|\mathbf x)=\sigma(\mathbf w_{wide}^T[\mathbf x,\phi(\mathbf x)]+\mathbf w_{deep}^T a^{(lf)}+b)
$$
$\sigma$是Sigmoid函数，$[\mathbf{x}, \phi(\mathbf{x})]$代表Wide部分的输入(包含原始特征和交叉特征)，$a^{(lf)}$是Deep部分最后一层的输出向量，$\mathbf{w}{wide}$，$\mathbf{w}{deep}$和$b$是最终预测层的权重和偏置

模型的梯度在反向传播时会同时更新Wide和Deep两部分的所有参数

由于两部分处理的特征类型不同，它们通常会采用不同的优化器

• Wide部分的输入特征非常稀疏，常使用带L1正则化的FTRL(Ferreira and Soares, 2025)等优化器，L1正则化可以产生稀疏的权重，相当于自动进行特征选择，让模型只“记住”重要的规则(惩罚某系参数置0)
• Deep部分的参数是稠密的，更适合使用像AdaGrad(Duchi et al., 2011)或Adam(Kingma and Ba, 2014)优化器

核心代码

# Wide部分：线性特征 + 交叉特征
linear_logit = get_linear_logits(input_layer_dict, feature_columns)
cross_logit = get_cross_logits(input_layer_dict, feature_columns)

# Deep部分：多个特征组的深度网络输出
deep_logits = []
for group_name, group_feature in group_feature_dict.items():
    deep_out = DNNs(units=dnn_units, activation="relu", dropout_rate=dnn_dropout_rate)(
        group_feature
    )
    deep_logit = tf.keras.layers.Dense(1, activation=None)(deep_out)
    deep_logits.append(deep_logit)

# 联合训练：将Wide和Deep的输出相加
wide_deep_logits = add_tensor_func(deep_logits + [linear_logit, cross_logit]) # list相加

# 最终预测：通过sigmoid函数输出点击概率
output = tf.keras.layers.Dense(1, activation="sigmoid")(wide_deep_logits)

Wide & Deep模型的意义不只是提供了一个新的网络结构，更重要的是给出了一个思路：怎么把记忆能力和泛化能力结合起来

该模型不仅成为了许多推荐业务的基线模型，更为后续精排模型的发展提供了重要的参考

特征交叉

Wide部分需要人工设计交叉特征，这种手工设计的方式不仅费时费力，还很难覆盖所有有用的特征组合

能否让模型自己学会做特征交叉呢？最直接的想法是让模型自动捕捉所有特征对之间的交互关系

但是推荐系统的特征动辄成千上万，如果每两个特征都要学一个参数，参数量会爆炸

而且推荐数据本身就很稀疏，大部分特征组合根本没有足够的样本来训练

关键是要找到一种巧妙的方法，既能自动学习特征交叉，又不会让参数太多

二阶特征交叉

FM: 从召回到精排

在召回时，FM主要解决的是“如何快速从海量物品中找到候选集”的问题

但在精排阶段问题是：如何自动学习特征之间的交叉关系，而不用手工一个个去设计

FM的核心思想发挥作用：给每个特征学一个向量表示，然后用向量内积来捕捉特征间的关系

为了捕捉特征间的交互关系，一个直接的想法是在线性模型的基础上增加所有特征的二阶组合项，即多项式模型：
$$
y = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^n w_{ij} x_i x_j
$$
这个模型存在两个致命缺陷：

• 参数数量会达到$O(n^2)$的级别，在特征数量庞大的推荐场景下难以承受
• 在数据高度稀疏的环境中，绝大多数的交叉特征$x_i x_j$在训练集中从未共同出现过，导致其对应的权重$w_{ij}$无法得到有效学习

FM 模型巧妙地解决了这个问题，它将交互权重分解为两个低维隐向量的内积$w_{ij}=\langle\mathbf v_i,\mathbf v_j\rangle$，模型的预测公式就演变为：
$$
y = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^n \langle\mathbf v_i,\mathbf v_j\rangle x_i x_j
$$
其中$\mathbf v_i,\mathbf v_j$ 分别是特征 $i$ 和特征 $j$ 的 $k$ 维隐向量(Embedding)，$k$ 是一个远小于特征数量 $n$ 的超参数

FM 的核心在于参数共享，相比直接为每一对特征学习独立的交叉权重 $w_{ij}$(复杂度为$O(n^2) $)，FM 只需为每个特征学习一个 $k$ 维隐向量，总参数量降低为 $O(nk)$

这种设计显著缓解了数据稀疏问题，即使特征 $i$ 和 $j$ 在训练样本中从未同时出现过，模型也能通过它们与其他特征的共现关系学到各自的隐向量，从而对二者的交叉效应进行合理预测

另外通过数学重写，FM 的二阶交叉项计算复杂度可从$O(kn^2)$优化到线性的$O(kn)$，使其在工业界得到了广泛应用

# FM层的核心计算：0.5 * ((sum(v))^2 - sum(v^2))
# inputs: [batch_size, field_num, embedding_size]

# 先求和再平方：(∑v_i)^2
square_of_sum = tf.square(
    tf.reduce_sum(inputs, axis=1, keepdims=True)
)  # [B, 1, D]

# 先平方再求和：∑(v_i^2)
sum_of_square = tf.reduce_sum(
    inputs * inputs, axis=1, keepdims=True
)  # [B, 1, D]

# FM二阶交互项
cross_term = 0.5 * tf.reduce_sum(
    square_of_sum - sum_of_square, axis=2
)  # [B, 1]

AFM：注意力加权的交叉特征

FM 对所有特征交叉给予了相同的权重，但实际上不同交叉组合的重要性是不同的

AFM(Xiao et al., 2017) 在 FM 的基础上引入注意力机制，为不同的特征交叉分配不同权重，使模型能够重点关注更有价值的交互

AFM 将所有成对特征的隐向量进行元素积(Hadamard Product)，得到保留向量信息的二阶交叉表示而不是像 FM 那样直接求内积，为后续的注意力计算提供了输入，这一步称为成对交互层(Pair-wise Interaction Layer)
$$
\color{purple}f_{PI}(\mathcal E)
= \sum_{(i,j)\in\mathcal R_x}
(\mathbf v_i \odot \mathbf v_j) x_i x_j
$$
$\mathcal E$ 表示输入样本中所有非零特征的embedding向量集合，$\mathcal R_x$ 表示输入样本中所有非零特征的索引对集合

AFM 使用一个小型注意力网络来学习每个交叉特征 $(v_i \odot v_j)$ 的重要性得分 $a_{ij}$
$$
\begin{aligned}
a_{ij}’ &= \textbf h^T \text{ReLU}(\textbf{W} (\mathbf v_i \odot \mathbf v_j) x_i x_j + \textbf{b}) \\
a_{ij} &= \frac{\exp(a_{ij}’)}{\sum_{(i,k) \in \mathcal R_x} \exp(a_{ik}’)}
\end{aligned}
$$
其中 $\textbf{W}$ 是注意力网络的权重矩阵，$\textbf{b}$ 是偏置向量，$\textbf{h}$ 是输出层向量

$\textbf{h}$是attention projection 向量[B, attention_factor, 1]，表示“什么样的交叉是重要的”这一判断标准

相当于一个不带激活的线性层，把输入映射成 1 维输出，几乎等价于Dense(1, use_bias=False)

得分 $a_{ij}$ 经过 Softmax 归一化后，被用作加权求和的权重，与原始的交叉特征向量相乘，最终汇总成一个向量，这个过程被称为注意力池化层(Attention-based Pooling)
$$
\color{red} f_{Att} = \sum_{(i,j) \in \mathcal R_x} a_{ij} (\mathbf v_i \odot \mathbf v_j) x_i x_j
$$
最终，AFM 将一阶线性部分与经过注意力加权的二阶交叉结果结合，输出预测结果
$$
\hat y_{afm}(x) = w_0 + \sum_{i=1}^n w_i x_i + \textbf{p}^T f_{Att}
$$
其中 $\textbf{p}$ 是一个投影向量，用于将最终的交叉结果映射为标量

通过引入注意力机制，AFM 不仅提升了模型的表达能力，还通过可视化注意力权重 $a_{ij}$ 赋予了模型更好的可解释性，可以洞察哪些特征交叉对预测结果的贡献最大

核心代码

# 1. 计算所有特征对的元素积交互
# num_pairs = n(n-1)/2
# group_pairwise: [batch_size, num_pairs, embedding_dim]
group_pairwise = pairwise_feature_interactions(
    group_feature, drop_rate=dropout_rate
) 

# 2. 注意力权重计算：h^T · ReLU(W · (v_i ⊙ v_j) + b) 
# 这个过程是FM没有的
weighted_inputs = tf.matmul(
    group_pairwise, attention_weight
) + attention_bias  # [B, num_pairs, attention_factor]

activation = tf.nn.relu(weighted_inputs)
# attention_projection是一个可学习的投影向量，用来把交互特征压缩成一个标量注意力分数
projected = tf.matmul(activation, attention_projection)  # [B, num_pairs, 1]

# 3. Softmax归一化得到注意力权重
attention_weights = tf.nn.softmax(projected, axis=1)

# 4. 加权求和：∑ a_ij · (v_i ⊙ v_j)
attention_output = tf.reduce_sum(
    tf.multiply(group_pairwise, attention_weights), axis=1
)  # [B, D]

相比FM对所有特征交叉一视同仁，AFM通过注意力机制自动识别重要的交互模式，提升了模型的表达能力和可解释性

NFM: 交叉特征的深度学习

NFM(Neural Factorization Machine) (He and Chua, 2017) 通过进一步利用特征交叉信息，在 FM 的基础上引入了深度网络。它将 FM 中得到的二阶交叉结果(以哈达玛积向量表示)作为输入，送入 DNN，从而学习更高阶、非线性的特征关系

其核心思想是：FM 学到的二阶交叉本身就是高质量特征，可作为 DNN 的输入，由深度网络自动建模这些交叉特征之间的复杂组合关系

NFM 的结构可以分为两个部分：先做特征交叉，再用深度网络学习

关键创新是引入“特征交叉池化层”(Bi-Interaction Pooling Layer)，把所有特征对的交叉信息汇总成一个向量，然后送给后面的神经网络去学习更复杂的模式。具体的计算过程如下：
$$
\color{purple}f_{BI}(V_x) = \sum_{i=1}^n \sum_{j=i+1}^n (\mathbf v_i \odot \mathbf v_j) x_i x_j
$$
其中 $V_x = {x_1 v_1, x_2 v_2, …, x_n v_n}$ 是输入样本中所有非零特征的 Embedding 向量集合，$\odot$ 仍然是元素积操作

这个操作的结果是一个与 Embedding 维度相同的向量，有效地编码了所有的二阶特征交叉信息

与FM中的变换类似，这一层的计算同样可以被优化到线性时间复杂度，非常高效：
$$
f_{BI}(V_x) = \frac{1}{2} \left[\left(\sum_{i=1}^n x_i \mathbf v_i\right)^2 - \sum_{i=1}^n (x_i \mathbf v_i)^2\right].
$$

虽然这里变为Hadamard Product，但是优化的方式是通用的，这里平方不是点积平方，而是逐元素平方

得到特征交叉池化层的输出向量 $f_{BI}(V_x)$ 后，NFM 将其送入一个标准的多层前馈神经网络(MLP)，输出$z_L$

最后，NFM 将一阶线性部分与 DNN 部分的输出结合起来，得到最终的预测结果：
$$
\hat y_{NFM}(x) = w_0 + \sum_{i=1}^n w_i x_i + \textbf h^T z_L
$$
其中 $\textbf h$ 是预测层的权重向量

维度	AFM	NFM
数学形式	线性映射 → 1 维	线性映射 → 1 维
输入对象	单个交叉向量	DNN 最终表示
输出语义	重要性分数	预测分数
是否参与 softmax	是	否
是否是模型输出	否	是
本质角色	Attention scorer	Prediction head

通过这种方式，NFM 巧妙地将 FM 的二阶交叉能力与 DNN 的高阶非线性建模能力结合在了一起

FM 可以被看作是 NFM 在没有隐藏层时的特例，这表明 NFM 是对 FM 的一个自然扩展和深度化

核心代码

# 双交互池化层：1/2 * ((∑v_i)^2 - ∑(v_i^2))
# inputs: [batch_size, num_features, embedding_dim]

# (∑v_i)^2：先求和再平方
sum_of_embeds = tf.reduce_sum(inputs, axis=1)  # [B, D]
square_of_sum = tf.square(sum_of_embeds)  # [B, D]

# ∑(v_i^2)：先平方再求和
square_of_embeds = tf.square(inputs)  # [B, N, D]
sum_of_square = tf.reduce_sum(square_of_embeds, axis=1)  # [B, D]

# 双交互池化输出
bi_interaction = 0.5 * (square_of_sum - sum_of_square)  # [B, D]

# 送入深度神经网络
dnn_output = DNNs(
    units=[64, 32], activation="relu", use_bn=True, dropout_rate=0.1
)(bi_interaction)

PNN: 多样化的乘积操作

PNN (Qu et al., 2016) 的核心动机很直接：单一的内积或元素积难以充分刻画特征交互，因此引入多种“乘积”操作，让模型更全面地建模特征之间的关系

PNN 的关键组件是乘积层(Product Layer)，该层以特征 Embedding 为输入，一方面保留线性信息，另一方面显式建模特征之间的二阶交互，并将两部分结果送入后续的全连接网络进行高阶非线性学习

PNN 的乘积层会产生两部分信号

一部分是线性信号 $\mathbf l_z$，本质上就是对所有特征 Embedding 的一次线性变换，可视为一个普通的全连接层
$$
\mathbf l_z^n = \sum_{i=1}^N\sum_{k=1}^M (\mathbf W_z^n)_{i,k} \mathbf f_i^k
$$
其中 $\mathbf f_i$ 是特征 $i$ 的 Embedding 向量，$\mathbf W_z^n$ 是第 $n$ 个神经元对应的线性信号权重矩阵，$N$ 为特征字段数量，$M$ 为 Embedding 维数

---

另一部分是二次信号 $\mathbf l_p$，用于刻画特征间的交互。根据交互方式不同，PNN 有两种主要变体

• IPNN (Inner Product-based Neural Network):

  使用特征 Embedding 之间的内积来计算二次信号
  $$
  \mathbf l_p^n = \sum_{i=1}^N \sum_{j=1}^N (\textbf W_p^n)_{i,j} \langle \mathbf f_i, \mathbf f_j \rangle
  $$
  $\mathbf W_p^n \in \mathbb R^{M \times M}$ 是第 $n$ 个神经元对应的权重矩阵，计算的复杂度是 $O(N^2)$，$N$ 为特征字段数量，复杂度太高

  利用将交互权重矩阵分解为向量外积的形式，$\textbf W_p^n$ 分解为 $\theta_n \theta_n^T$
  $$
  \mathbf l_p^n = \sum_{i=1}^N \sum_{j=1}^N \theta_i^n \theta_j^n \langle \mathbf f_i, \mathbf f_j \rangle = \sum_{i=1}^N \sum_{j=1}^N \langle \theta_i^n \mathbf f_i, \theta_j^n \mathbf f_j \rangle = \langle \sum_{i=1}^N \theta_i^n \mathbf f_i, \sum_{j=1}^N \theta_j^n \mathbf f_j \rangle = \left|\sum_{i=1}^N \theta_i^n \mathbf f_i\right|^2
  $$
  通过这个变换，所有内积对的加权和转变成了先对 Embedding 进行加权求和，然后计算一次向量的 L2 范数平方，复杂度成功地从 $O(N^2M)$ 降低到了 $O(NM)$
  $$
  \mathbf l_p = \left(\left|\sum_{i=1}^N \theta_i^1 \mathbf f_i\right|^2, \left|\sum_{i=1}^N \theta_i^2 \mathbf f_i\right|^2, \ldots, \left|\sum_{i=1}^N \theta_i^n \mathbf f_i\right|^2\right)
  $$

• OPNN (Outer Product-based Neural Network):

  使用特征 Embedding 之间的外积来捕捉更丰富的交互信息

  如果对所有外积对进行加权求和$\sum_{i=1}^N \sum_{j=1}^N \mathbf{f}_i \mathbf{f}_j^T$，计算复杂度太高$O(N^2M^2)$

  OPNN 采用了一种称为“叠加”(superposition)的近似方法来大幅降低复杂度

  先将所有特征的 Embedding 向量相加，然后再计算一次外积
  $$
  \sum_{i=1}^N \sum_{j=1}^N \mathbf f_i \mathbf f_j^T = (\sum_{i=1}^N \mathbf f_i)(\sum_{j=1}^N \mathbf f_j)^T
  $$
  计算量得到了节省$O(M(M+N)) = O(NM)+O(M^2)$
  $$
  \mathbf l_p = \left(\langle\mathbf W_p^1, (\sum_{i=1}^N \mathbf f_i)(\sum_{j=1}^N \mathbf f_j)^T\rangle, \langle\mathbf W_p^2, (\sum_{i=1}^N \mathbf f_i)(\sum_{j=1}^N \mathbf f_j)^T\rangle, \ldots, \langle\mathbf W_p^n, (\sum_{i=1}^N \mathbf f_i)(\sum_{j=1}^N \mathbf f_j)^T\rangle\right)
  $$

在得到线性信号 $l_z$ 和经过优化的二次信号 $l_p$ 后，PNN 将它们合并，并送入后续的全连接层进行高阶非线性变换
$$
\begin{aligned}
\mathbf l_1 &= \text{ReLU}(\mathbf l_z + \mathbf l_p + \mathbf b_1) \\
\mathbf l_2 &= \text{ReLU}(\mathbf W_2 \mathbf l_1 + \mathbf b_2) \\
\hat y &= \sigma(\textbf W_3 \mathbf l_2 + b_3)
\end{aligned}
$$
PNN 的独特之处在于，它将“乘积”操作(无论是内积还是外积)作为了网络中的一个核心计算单元，认为这种操作比传统 DNN 中简单的“加法”操作更能有效地捕捉类别型特征之间的交互关系

---

核心代码

以IPNN的优化实现为例

# 线性信号：直接对特征embedding做全连接
concat_embed = tf.concat(inputs, axis=1)  # [B, N*D]
lz = tf.matmul(concat_embed, linear_w)  # [B, units]

# 内积优化：||∑(θ_i · f_i)||^2 代替 ∑∑<θ_i·f_i, θ_j·f_j>
lp_list = []
for i in range(units):
    # 对每个特征加权：θ_i · f_i
    delta = tf.multiply(
        concat_embed, tf.expand_dims(inner_w[i], axis=1)
    )  # [B, N, D]

    # 求和后计算L2范数平方：||∑(θ_i · f_i)||^2
    delta = tf.reduce_sum(delta, axis=1)  # [B, D]
    lp_i = tf.reduce_sum(tf.square(delta), axis=1, keepdims=True)  # [B, 1]
    lp_list.append(lp_i)

# 拼接线性信号和内积信号
lp = tf.concat(lp_list, axis=1)  # [B, units]
product_output = tf.concat([lz, lp], axis=1)  # [B, 2*units]

FiBiNET: 特征重要性与双线性交互

PNN 用了多种乘积操作来做特征交互，但默认所有特征的重要性相同

FiBiNET (Feature Importance and Bilinear feature Interaction Network) (Huang et al., 2019) 针对这一不足，引入特征重要性建模机制，在交互之前先学习各特征的权重，再有针对性地进行特征交互

FiBiNET 的创新主要体现在两个核心模块上：SENET 特征重要性学习机制和双线性交互层

SENET 特征重要性学习

FiBiNET 引入 SENET(Squeeze-and-Excitation Network)(Hu et al., 2018) 机制，用于自适应学习不同特征的重要性权重。与传统方法对所有特征一视同仁不同，SENET 能根据当前任务自动调整各特征的关注程度

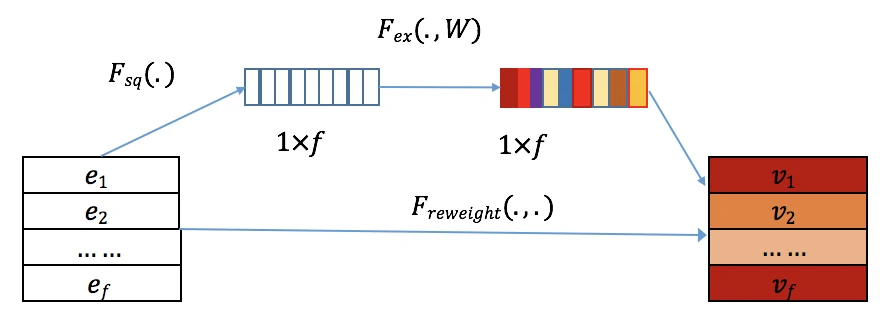
SENET 的工作流程分为三个步骤：

1. Squeeze (挤压): 对每个特征的 embedding 向量做全局平均池化，将高维向量压缩为一个标量表示
   $$
   \mathbf z_i = F_{\text{sq}}(\mathbf e_i) = \frac{1}{k} \sum_{t=1}^k \mathbf e_i(t)
   $$

2. Excitation (激活): 通过一个小型两层神经网络，建模特征之间的依赖关系，输出每个特征的重要性权重
   $$
   \mathbf A = F_{\text{ex}}(\mathbf Z) = \sigma_2(\mathbf W_2 \sigma_1(\mathbf W_1 \mathbf Z))
   $$
   其中 $\mathbf W_1 \in \mathbb R^{f \times \frac{f}{r}}$ 和 $\mathbf W_2 \in \mathbb R^{\frac{f}{r} \times f}$ 是可学习的权重矩阵，$r$ 是缩减率超参数

3. Re-weight (重新加权): 利用学到的权重对原始 embedding 进行缩放，突出重要特征，抑制次要特征
   $$
   \mathbf V = F_{\text{ReWeight}}(\mathbf A, \mathbf E) = [\mathbf a_1 \cdot \mathbf e_1, \mathbf a_2 \cdot \mathbf e_2, \ldots, \mathbf a_f \cdot \mathbf e_f]
   $$

经过 SENET 处理后，模型获得了一组带有重要性信息的特征嵌入表示

双线性交互层

在获得原始嵌入 $\mathbf E$ 和经过 SENET 加权的嵌入，FiBiNET 接下来要解决如何更好地建模特征交互的问题

不同于 FM 的内积或 PNN 的元素积，FiBiNET 采用双线性交互，引入一个可学习的变换矩阵$\mathbf W \in \mathbb R^{k \times k}$
$$
\mathbf p_{ij} = \mathbf v_i \cdot \mathbf W \circ \mathbf v_j
$$
其中 $\circ$ 表示哈达玛积，这种双线性变换相比于简单的内积或元素积，能够捕捉到更加丰富和细致的特征交互信息

FiBiNET 同时对原始嵌入 $\mathbf{E}$ 和加权嵌入 $\mathbf{V}$ 进行双线性交互，并将这些交互结果与深度网络输出共同用于预测

通过这种方式，FiBiNET 不仅解决了”哪些特征更重要”的问题，还通过双线性交互提升了二阶特征交叉的表达能力

核心代码

# 1. SENET特征重要性学习
# inputs: [batch_size, num_features, embedding_dim]

# Squeeze：全局平均池化
squeeze = tf.reduce_mean(inputs, axis=-1)  # [B, N]

# Excitation：两层全连接网络
excitation = tf.matmul(squeeze, w1)  # [B, reduction_size]
excitation = tf.nn.relu(excitation)
excitation = tf.matmul(excitation, w2)  # [B, N]
excitation = tf.nn.sigmoid(excitation)

# Re-weight：应用注意力权重
excitation = tf.expand_dims(excitation, axis=2)  # [B, N, 1]
senet_output = tf.multiply(inputs, excitation)  # [B, N, D]

# 2. 双线性交互：v_i · W ⊙ v_j
interaction_outputs = []
for i in range(num_features):
    for j in range(i+1, num_features):
        # 对特征i应用变换矩阵
        vi_transformed = tf.matmul(inputs[:, i, :], W_list[idx])  # [B, D]
        # 与特征j做元素积
        interaction = tf.multiply(vi_transformed, inputs[:, j, :])  # [B, D]
        interaction_outputs.append(interaction)

DeepFM: 低阶高阶的统一建模

DeepFM (Guo et al., 2017) 是在 Wide & Deep 架构上的直接改进，用 FM 模型替代了需要大量人工特征工程的 Wide 部分，从而实现了真正的端到端训练

DeepFM 的一个关键设计：FM 组件和 Deep 组件共享同一套特征 Embedding

模型可以在同一表示空间中同时学习低阶和高阶特征交互，不仅减少了参数冗余，也提升了训练效率

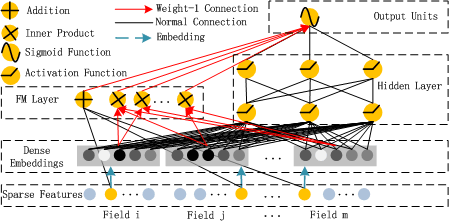
DeepFM 由两个并行组件构成：

• FM 组件: 负责学习一阶特征和二阶特征交叉，其输出的计算方式与标准 FM 完全相同，用于捕捉低阶交互关系
  $$
  y_{FM} = \langle w, x \rangle + \sum_{i=1}^{n} \sum_{j=i+1}^{n}\left\langle\mathbf v_{i}, \mathbf v_{j}\right\rangle x_{i} x_{j}
  $$

• Deep 组件: 以 FM 中使用的 Embedding 向量作为输入，将各特征的 Embedding 拼接后送入前馈神经网络，学习高阶、非线性的特征交互模式
  $$
  a^{(l+1)} = \sigma(\textbf W^{(l)} a^{(l)} + \textbf b^{(l)})
  $$
  其中 $l$ 是层深度，$\sigma$ 是激活函数，$\textbf W^{(l)}$、$\textbf b^{(l)}$分别是第 $l$ 层的权重和偏置，最后输出为
  $$
  y_{Deep} = \textbf W^{|H|+1} \cdot a^{|H|} + \textbf b^{|H|+1}
  $$
  其中 $H$ 是隐藏层数量

最终，DeepFM 将 FM 部分和 Deep 部分输出的 logit 直接相加，并通过 Sigmoid 函数得到点击率预测
$$
\hat y = \sigma(y_{FM} + y_{Deep})
$$
DeepFM 的核心思路很简单：用 FM 自动学习低阶特征交互，用 DNN 学习高阶特征交互，并通过共享 Embedding 将两者紧密结合

相比 Wide & Deep，DeepFM 显著减少了人工特征工程的依赖，使模型更加简洁且易于扩展

核心代码

# 获取共享的特征embedding
# concat_feature: [batch_size, num_features, embedding_dim]
concat_feature = concat_group_embedding(
    group_embedding_feature_dict, group_name, axis=1, flatten=False
) # 这里不flatten是为了FM，需要显示计算特征交叉

# 1. FM组件：学习二阶特征交叉
fm_output = FM()(concat_feature)  # [B, 1]

# 2. DNN组件：学习高阶非线性特征交叉
# 将embedding展平作为DNN输入
flatten_feature = tf.keras.layers.Flatten()(concat_feature)  # [B, N*D]
dnn_output = DNNs(
    units=[64, 32, 1],  # 多层神经网络
    activation="relu",
    dropout_rate=0.1
)(flatten_feature)  # [B, 1]

# 3. 联合训练：将FM和DNN的输出相加
deepfm_logits = tf.add(fm_output, dnn_output)  # [B, 1]
output = tf.keras.layers.Dense(1, activation="sigmoid")(deepfm_logits)

DeepFM通过共享Embedding实现了端到端训练，FM组件捕捉低阶交叉，DNN组件学习高阶模式，两者互补形成高效的特征学习能力

总结

模型	二阶交叉方式	是否区分重要性	是否建模高阶
FM	内积	❌	❌
AFM	Hadamard + Attention	✅	❌
NFM	Hadamard + DNN	❌	✅
PNN	内积 / 外积	❌	✅
FiBiNET	双线性交互	✅	✅
DeepFM	FM + DNN	❌	✅

虽然有些方法建模了高阶，但它们并不是显示地建模高阶，都是利用FM显示建模二阶，利用 DNN 隐式建立高阶模型

对比NFM和DeepFM

维度	NFM	DeepFM
显式二阶交叉	有	有
高阶交叉来源	二阶交叉的非线性组合	原始特征的隐式交叉
是否保留原始特征	否	是
交叉空间	固定（二阶）	自由（≥3 阶）

• NFM 的深度是“交叉后再加深”
• DeepFM 的深度是“保留原始信息再自动交叉”

高阶特征交叉

深度网络虽然能学到高阶交互，但不知道它具体学到了什么，也不清楚这些交互是怎么影响预测的

能不能像 FM 处理二阶交叉那样，设计出能够明确捕捉高阶交叉的网络结构？

DCN: 残差连接的高阶交叉

Deep & Cross Network (DCN) (Wang et al., 2017) 用Cross Network替代了Wide & Deep模型中需要人工构造特征的 Wide 部分，实现了显式、高效的高阶特征交叉建模

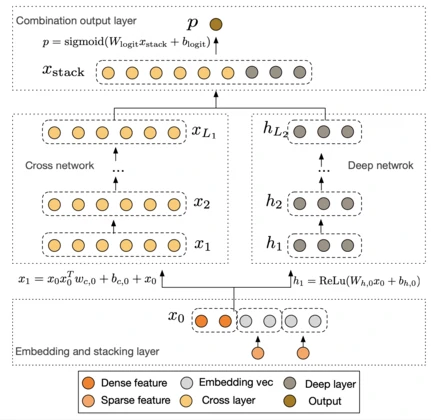
DCN 的整体结构由两条并行分支组成：

• Cross Network：显式建模特征交叉
• Deep Network：学习隐式的高阶非线性关系

两者共享同一套 Embedding 作为输入

首先，模型将稀疏的类别特征转换为低维稠密的Embedding向量，并与数值型特征拼接在一起，形成统一的输入向量$\mathbf x_0$
$$
\mathbf x_0 = [\mathbf x_{\text{embed}, 1}^T, \ldots, \mathbf x_{\text{embed}, k}^T, \mathbf x_{\text{dense}}^T]
$$
这个初始向量会被同时送入Cross Network和Deep Network

Cross Network是DCN的核心创新，它由多个交叉层堆叠而成，其精妙之处在于每一层的计算都会与原始输入$\mathbf x_0$的直接交互
$$
\mathbf x_{l+1} = \mathbf x_0 \mathbf x_l^T \mathbf w_l + \mathbf b_l + \mathbf x_l
$$

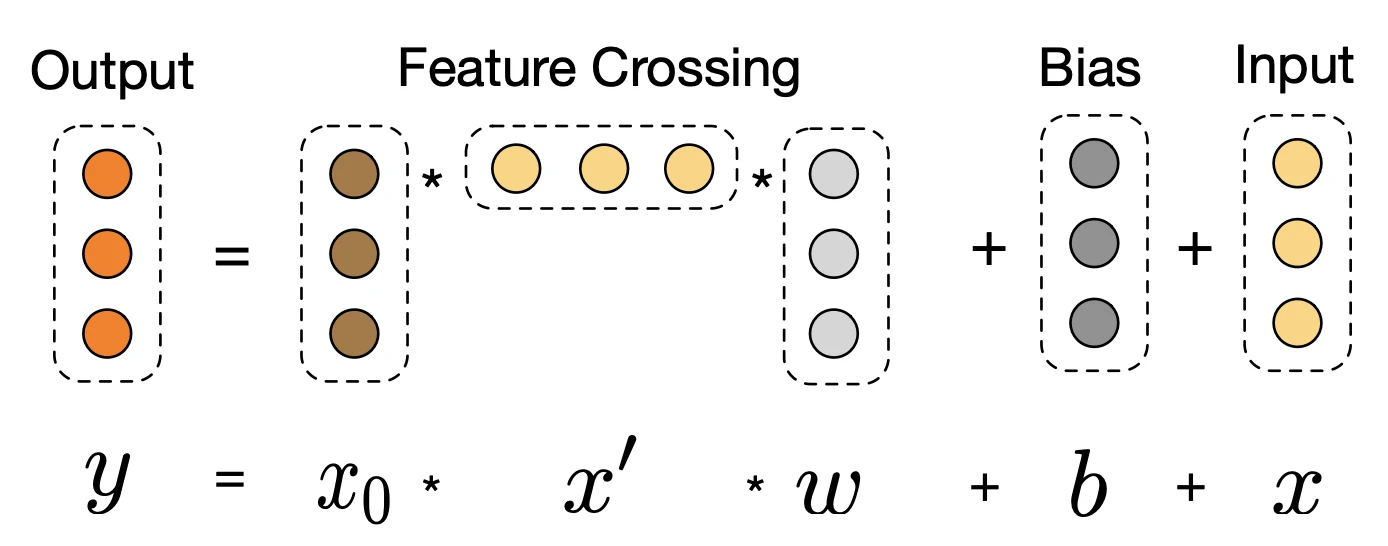
这一结构可以看作一种带显式交叉项的残差网络：

• $\mathbf x_l$：残差连接，保证信息稳定传递
• $\mathbf x_0 \mathbf x_l^T \mathbf w_l$：显式特征交叉项

例如：在第一层($l=0$)，$\mathbf x_1$ 包含了与 $\mathbf x_0$ 相关的二阶交叉项；在第二层($l=1$)，由于 $\mathbf x_1$ 已经包含了二阶信息，它与 $\mathbf x_0$ 的再次交叉就会产生三阶的交叉项

因此，Cross Network 的深度直接决定了可建模的最高交叉阶数

这种设计使得参数量只随着输入维度呈线性增长，非常高效

与Cross Network并行的Deep Network部分是一个标准的全连接神经网络，用于隐式地学习高阶非线性关系，其结构与DeepFM中的DNN部分类似

最后模型将Cross Network的输出 $\mathbf x_{L_1}$ 和Deep Network的输出 $\mathbf h_{L_2}$ 拼接起来，通过一个逻辑回归层得到最终的预测概率

# Cross Network的交叉层：x_{l+1} = x_0 * (x_l^T * w_l) + b_l + x_l
# 输入 x_0: [batch_size, feature_dim]

x_l = x_0  # 初始化为原始输入
for i in range(num_cross_layers):
    # 计算 x_l^T * w_l：得到一个标量权重
    xlw = tf.matmul(x_l, w_l)  # [B, 1]

    # 计算 x_0 * (x_l^T * w_l)：交叉项
    cross_term = tf.multiply(x_0, xlw)  # [B, D]

    # 残差连接：x_{l+1} = cross_term + b_l + x_l
    x_l = cross_term + b_l + x_l  # [B, D]

xDeepFM: 向量级别的特征交互

DCN 虽然能够显式构建高阶特征交叉，但其交叉发生在元素级别(bit-wise)，Embedding向量中的每个元素都单独和其他特征的元素交互，这样就把Embedding向量拆散了，没有把它当作一个完整的特征来看待

为此，xDeepFM 提出了压缩交互网络(Compressed Interaction Network, CIN)(Lian et al., 2018) ，以向量级别(vector-wise)的方式进行显式特征交叉

xDeepFM 由三部分并行组成：

• 线性部分：建模一阶特征
• DNN 部分：学习隐式、高阶非线性交互
• CIN 部分：学习显式、向量级的高阶特征交叉

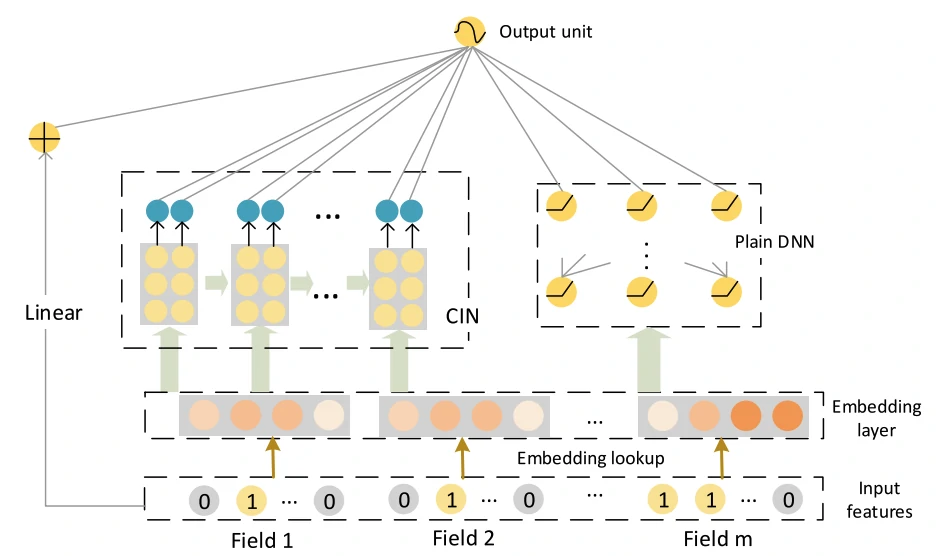
CIN 的输入是一个特征域级别的 Embedding 矩阵
$$
\mathbf X_0 \in \mathbb R^{m \times D}
$$

• $m$：特征域(Field)数量
• $D$：Embedding 维度
• 第$i$行$\mathbf e_i$：第 $i$ 个特征域的 Embedding 向量

CIN 通过多层堆叠来显式建模高阶交叉，第 $k$ 层的输出 $\mathbf X_k$ 为上一层的输出 $\mathbf X_{k-1}$ 和最原始的输入 $\mathbf X_0$

1. 模上一层输出的$H_{k-1}$个向量与原始输入层的 $m$ 个向量之间，两两做Hadamard Product

   这个操作会产生 $H_{k-1} \times m$ 个交互向量，每个向量的维度仍然是 $D$

2. 为了生成第 $k$ 层的第 $h$ 个新特征向量 $\mathbf X_{h,\ast}^k$，模型对所有交互向量进行加权求和
   $$
   \mathbf X_{h,\ast}^k = \sum_{i=1}^{H_{k-1}} \sum_{j=1}^{m} \mathbf W_{i,j}^{k,h} (\mathbf X_{i,\ast}^{k-1} \circ \mathbf X_{j,\ast}^0)
   $$
   其中：

   • $\mathbf X_k \in \mathbb R^{H_k \times D}$ ：CIN 第 $k$ 层的输出，包含了 $H_k$ 个特征向量的集合(称为“特征图”)，$H_k$ 是第 $k$ 层特征图的数量

   • $\mathbf X_{i,\ast}^{k-1}$：第 $k-1$ 层输出的第 $i$ 个 $D$ 维向量

   • $\mathbf X_{j,\ast}^0$ ：原始输入矩阵的第 $j$ 个 $D$ 维向量(即第 $j$ 个特征域的Embedding)

   • $\circ$：哈达玛积，实现了向量级别的交互，保留了 $D$ 维的向量结构

   • $\mathbf W_{k,h} \in \mathbb R^{H_{k-1} \times m}$：参数矩阵，它为每一个由 $(\mathbf X_{i,\ast}^{k-1}, \mathbf X_{j,\ast}^0)$ 产生的交互向量都提供了一个权重，通过加权求和的方式，将 $H_{k-1} \times m$ 个交互向量的信息“压缩”成一个全新的 $D$ 维向量 $\mathbf X_{h,*}^k$

在计算出每一层(从第$1$层到第$T$层)的特征图 $\mathbf X_k$ 后，CIN会对每个特征图的所有向量在维度$D$上进行求和池化(Sum Pooling)，得到一个池化后的向量 $\mathbf p_k \in \mathbb R^{H_k}$

将所有层的池化结果拼接，形成 CIN 的最终输出
$$
\mathbf p^+ = [\mathbf p_1, \mathbf p_2, \ldots, \mathbf p_T]
$$
该向量显式包含二阶到$T+1$阶的向量级交叉特征

最终，xDeepFM将线性部分、DNN部分和CIN部分的输出结合起来，通过一个Sigmoid函数得到最终的预测结果
$$
\hat y = \sigma(\mathbf w_\text{linear}^T \mathbf a + \mathbf w_\text{dnn}^T \mathbf x_\text{dnn}^k + \mathbf w_\text{cin}^T \mathbf p^+ + \mathbf b)
$$
通过CIN网络，xDeepFM把向量级别的显式交互和元素级别的隐式交互结合到了一起，为高阶特征交互提供了一个更好的解决方案

# CIN层的向量级别交互
# inputs: [batch_size, field_num, embed_dim]

cin_layers = [inputs]  # X^0：原始输入
pooled_outputs = []

for layer_size in cin_layer_sizes: # cin_layer_sizes = [H1, H2, H3]
    # 获取上一层输出 X^{k-1} 和原始输入 X^0
    x_k_minus_1 = cin_layers[-1]  # [B, H_{k-1}, D]
    x_0 = cin_layers[0]  # [B, m, D]

    # 扩展维度以便进行广播计算
    x_k_minus_1_expand = tf.expand_dims(x_k_minus_1, axis=2)  # [B, H_{k-1}, 1, D]
    x_0_expand = tf.expand_dims(x_0, axis=1)  # [B, 1, m, D]

    # 向量级别的哈达玛积交互
    z_k = tf.multiply(x_k_minus_1_expand, x_0_expand)  # [B, H_{k-1}, m, D]

    # 压缩：通过线性变换将 H_{k-1}*m 个交互向量压缩为 H_k 个
    z_k_reshape = tf.reshape(z_k, [batch_size, -1, embed_dim])  # [B, H_{k-1}*m, D]
    x_k = dense_layer(tf.transpose(z_k_reshape, [0, 2, 1]))  # [B, D, H_k]
    x_k = tf.transpose(x_k, [0, 2, 1])  # [B, H_k, D]

    cin_layers.append(x_k)

    # 求和池化：将向量维度聚合为标量
    pooled_outputs.append(tf.reduce_sum(x_k, axis=-1))  # [B, H_k]

# 拼接所有层的输出
cin_output = tf.concat(pooled_outputs, axis=1)  # [B, sum(H_k)]

AutoInt: 自注意力的自适应交互

DCN 通过残差结构实现了元素级别的显式高阶特征交叉，xDeepFM 通过 CIN 实现了向量级别的显式高阶交叉，但二者都有一个共同局限：高阶特征交互的构建方式是预先固定的

• DCN：每一层都必须与原始输入交叉
• CIN：交互对象和交互形式由网络结构提前定义

能否让模型自动决定“哪些特征要交互、交互强度有多大”？

AutoInt (Automatic Feature Interaction) (Song et al., 2019) 借鉴 Transformer 的核心思想，引入 多头自注意力机制，在训练过程中自适应地学习任意阶数的特征交互，而不依赖固定的交互公式或人工设计的结构

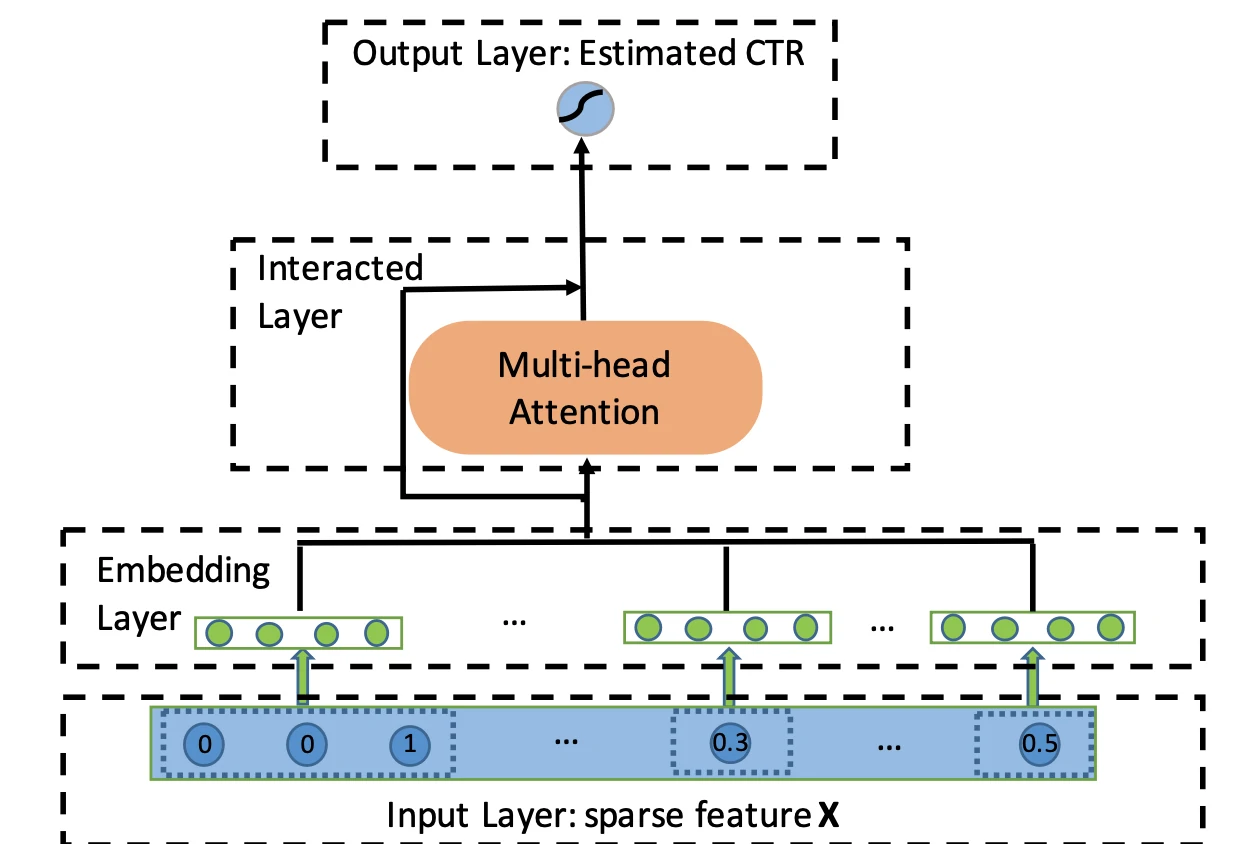
AutoInt 首先将所有特征(类别型与数值型)映射为同一维度的嵌入向量$\mathbf e_m \in \mathbb R^d$，其中 $m$ 代表第 $m$ 个特征域

所有特征嵌入共同构成自注意力层的输入，角色上等价于 Transformer 中的 token embeddings

多头自注意力机制

AutoInt 的核心是其交互层，该层由多头自注意力机制构成

对于任意两个特征的嵌入向量 $\mathbf e_m$ 和 $\mathbf e_k$，自注意力机制会计算它们之间的相关性得分，这个过程在每个”注意力头” (head) $h$ 中独立进行
$$
\alpha_{m,k}^{(h)} = \frac{\exp(\psi^{(h)}(\mathbf e_m, \mathbf e_k))}{\sum_{l=1}^{M}\exp(\psi^{(h)}(\mathbf e_m, \mathbf e_l))}
$$
其中相似度函数通常采用缩放点积注意力
$$
\psi^{(h)}\left(\mathbf e_{\mathbf m}, \mathbf e_{\mathbf k}\right)=\left\langle\mathbf W_{\text {Query }}^{(h)} \mathbf e_{\mathbf m}, \mathbf W_{\text {Key }}^{(h)} \mathbf e_{\mathbf k}\right\rangle
$$
在得到注意力权重后，模型对 Value 向量进行加权求和，生成一个新的、融合了其他特征信息的表示
$$
\mathbf {\tilde e_m^{(h)}} = \sum_{k=1}^{M} \alpha_{m,k}^{(h)} (\mathbf{W}_{\text{Value}}^{(h)} \mathbf{e}_k)
$$
该表示本质上是由模型自动学习得到的“特征组合结果”

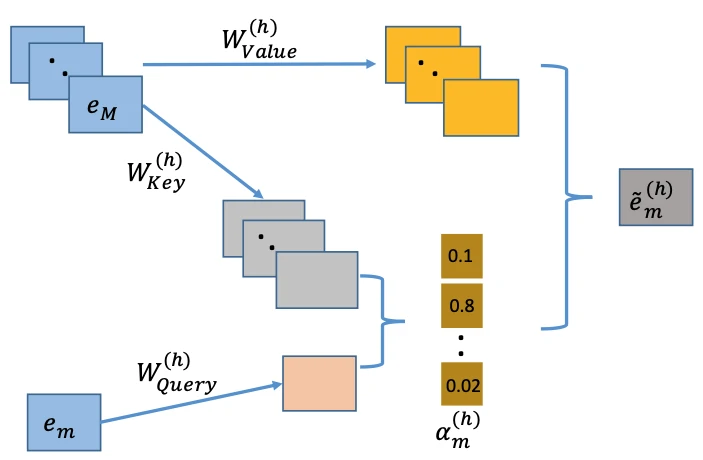
多层交互与高阶特征学习

“多头”机制允许模型在不同的子空间中并行地学习不同方面的特征交互，各注意力头的输出被拼接，形成更丰富的表示：
$$
\mathbf{\tilde e_m} = \mathbf{\tilde e_m^{(1)}} \oplus \mathbf{\tilde e_m^{(2)}} \oplus \cdots \oplus \mathbf{\tilde e_m^{(H)}}
$$
为了稳定训练并保留原始信息，引入残差连接：
$$
\mathbf{e_m^{\text{Res}}}= \text{ReLU}(\mathbf e_m + \mathbf W_{\text{Res}} \mathbf{\tilde{e}_m)}
$$
AutoInt 的关键创新在于其高阶特征交互的构建方式

通过堆叠多个这样的交互层，AutoInt 能够显式地构建任意高阶的特征交互，每一层的输出都代表了更高一阶的、自适应学习到的特征组合

与 DCN、xDeepFM 不同，AutoInt 中的高阶交互：

• 不依赖固定公式
• 不依赖预设结构
• 而是由注意力权重动态决定

所有层输出的特征表示被拼接后，送入逻辑回归层进行预测
$$
\hat y=\sigma\left(\mathbf w^{\mathrm T}\left(\mathbf e_{1}^{\mathbf{Res}} \oplus \mathbf e_{2}^{\mathbf{Res}} \oplus \cdots \oplus \mathbf e_{\mathbf{M}}^{\text {Res}}\right)+b\right)
$$
AutoInt 的优势总结

• 交互方式灵活：模型自主决定交互关系
• 可解释性强：注意力权重可直接反映特征重要性
• 高阶能力自然：层数即交叉阶数

# 多头自注意力层的前向传播
# inputs: [batch_size, num_features, embed_dim]

head_outputs = []
for i in range(num_heads):
    # 计算Query、Key、Value矩阵
    query = tf.einsum('bfe,ea->bfa', inputs, query_weights[i])  # [B, N, d']
    key = tf.einsum('bfe,ea->bfa', inputs, key_weights[i])      # [B, N, d']
    value = tf.einsum('bfe,ea->bfa', inputs, value_weights[i])  # [B, N, d']

    # 计算注意力得分：Query和Key的点积
    attention_score = tf.matmul(query, key, transpose_b=True)  # [B, N, N]

    # Softmax归一化得到注意力权重
    attention_weights = tf.nn.softmax(attention_score, axis=-1)  # [B, N, N]

    # 加权求和：用注意力权重对Value进行聚合
    head_output = tf.matmul(attention_weights, value)  # [B, N, d']
    head_outputs.append(head_output)

# 拼接多个注意力头的输出
multi_head_output = tf.concat(head_outputs, axis=-1)  # [B, N, d'*H]

# 残差连接：保留原始信息
residual_input = tf.tensordot(inputs, residual_weights, axes=[[2], [0]])
output = tf.keras.layers.ReLU()(multi_head_output + residual_input)

总结

DCN：用 Cross Layer 构造显式的多项式特征交叉

关键公式：
$$
\mathbf x_{l+1} = \mathbf x_0 \mathbf x_l^T \mathbf w_l + \mathbf b_l + \mathbf x_l
$$

• 显式多项式交叉，阶数完全可控，参数效率高（低秩），在bit-wise维度上交互

• 交叉形式固定（外积结构），表达多样性有限

xDeepFM：在 embedding 级别显式构造高阶交叉

关键模块CIN：
$$
\mathbf X^{(k)} = f(\mathbf X^{(k-1)}\circ \mathbf X^{(0)})
$$

• 显式、逐阶构造交叉；交叉粒度在 vector-level；可枚举
• 计算和显存开销大

AutoInt：用 Self-Attention 自动学习特征交叉权重

关键机制：
$$
\text{Attention}(Q,K,V) = \text{softmax}\left (\frac{QK^T}{\sqrt d} \right)V
$$

• 自动选择交叉关系；不需要人工设定交叉结构
• 交叉阶数不直观；解释性弱于 DCN / xDeepFM

维度	DCN	xDeepFM	AutoInt
交叉方式	多项式	枚举式	注意力
是否显式	是	是	半显式
阶数可控	强	强	弱
表达自由度	中	高	高
参数效率	高	中	中
可解释性	高	中	中偏低

序列建模

无论是二阶交叉的FM、AFM，还是高阶交叉的DCN、xDeepFM，它们的核心目标都是从一个静态的特征集合中挖掘出有价值的信息

这些模型存在一个共同的局限：它们大多将用户的历史行为看作无序的，如同用户的兴趣是一个静态的表示

传统的特征交叉模型难以捕捉这种蕴含在行为顺序中的、随时间变化的意图

序列建模不再将用户历史看作一堆静态特征的集合，而是将其视为一个动态的序列，介绍工业界在序列建模方向上的三个代表性模型：DIN、DIEN和DSIN

DIN:局部激活的注意力机制

在传统的深度学习模型(即Embedding&MLP范式)中，通常的做法是将用户所有的历史行为(如点击过的商品ID)对应的Embedding向量通过池化(Pooling)操作，压缩成一个固定长度的向量来代表该用户

这个固定长度的用户向量，很快就成为了表达用户多样兴趣的瓶颈

为了增强表达能力而粗暴地增加向量维度，又会带来参数量爆炸和过拟合的风险

DIN的核心思想：局部激活 (Local Activation)

深度兴趣网络(Deep Interest Network, DIN)(Zhou et al., 2018)发现，用户的某一次具体点击行为，通常只由其历史兴趣中的一部分所“激活”，所以用户的兴趣表示不应该是固定的，而应是根据当前的候选广告(Candidate Ad)不同而动态变化的

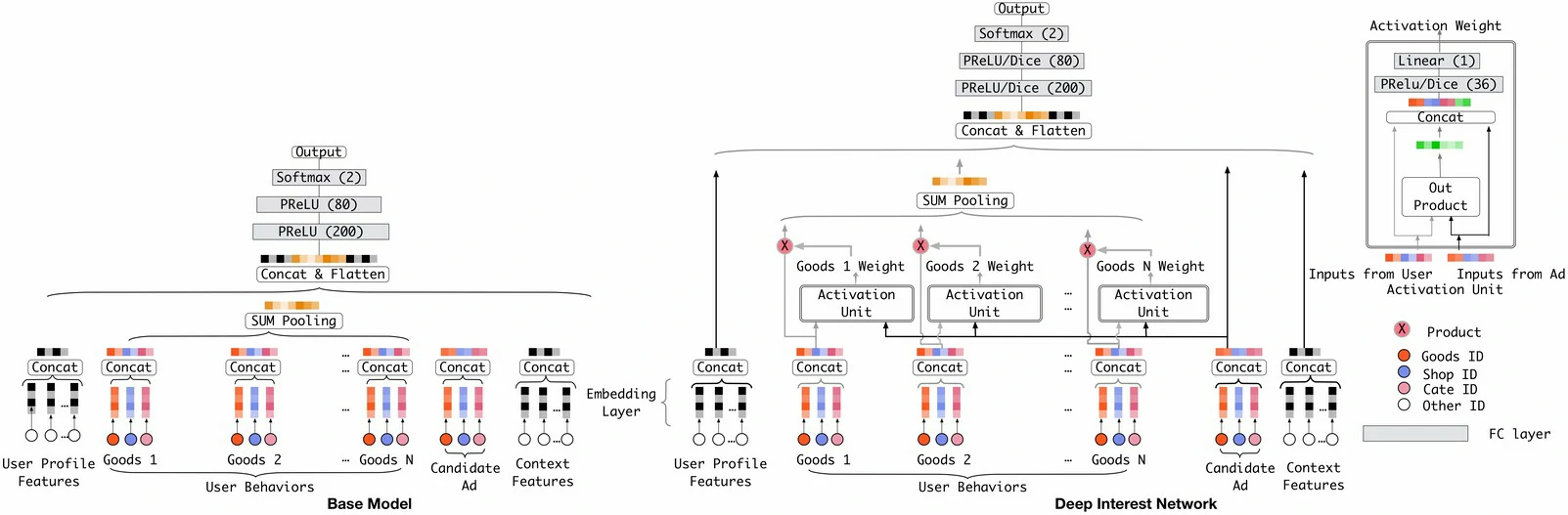
为了实现“局部激活”这一思想，DIN引入了局部激活单元(Local Activation Unit)，其本质就是注意力机制

与基准模型对用户历史行为 Embedding 做简单池化不同，DIN 会根据候选广告对历史行为进行加权求和，从而得到与当前广告相关的用户兴趣表示

具体来说，对于一个给定的用户$U$和候选广告$A$，用户的兴趣表示向量$\boldsymbol v_{U}(A)$定义为
$$
\boldsymbol v_{U}(A)=f(\boldsymbol v_{A},\boldsymbol e_{1},\boldsymbol e_{2},\ldots,\boldsymbol e_{H})=\sum_{j=1}^{H}a(\boldsymbol e_{j},\boldsymbol v_{A})\boldsymbol e_{j}=\sum_{j=1}^{H}w_{j}\boldsymbol e_{j}
$$

• $\boldsymbol e_{j}$表示用户的第$j$个历史行为 Embedding

• $\boldsymbol v_{A}$ 是候选广告A的Embedding向量

• $a(\boldsymbol e_{j}, \boldsymbol v_{A})$ 是一个激活单元(通常是一个小型前馈神经网络)，用于计算历史行为与广告之间的相关性权重$\boldsymbol w_{j}$

  该权重刻画了历史行为在当前广告场景下的重要程度，与广告越相关的历史行为，其对应权重越大，在最终兴趣表示中贡献也越高

DIN 学到的用户兴趣表示不再是固定向量，而是随候选广告动态变化的

需要注意的是，DIN 中的注意力权重未使用 Softmax 归一化，$\sum \boldsymbol w_{j}$不一定等于1，这种设计可以保留用户兴趣的绝对强度信息：当大量历史行为与广告高度相关时，加权后的兴趣向量模长更大；反之则更小

这样不仅能刻画兴趣的方向，还能反映兴趣的强弱

# DIN注意力层的核心计算
# query: 候选广告 [batch_size, 1, embedding_dim]
# keys: 历史行为序列 [batch_size, seq_len, embedding_dim]

query = tf.squeeze(query, axis=1)  # [B, H]
length = tf.shape(keys)[-2]
query = tf.expand_dims(query, axis=1)  # [B, 1, H]

# 构建多角度交互特征：query, keys, query-keys, query*keys
att_inputs = tf.concat([
    tf.tile(query, [1, length, 1]),  # 重复query以匹配序列长度
    keys,                             # 历史行为
    query - keys,                     # 差异特征
    query * keys                      # 元素积特征
], axis=-1)  # [B, L, 4*H]

# 通过前馈网络计算注意力分数
hidden_layer = ffn_layer(att_inputs)  # [B, L, hidden_units]
scores = tf.keras.layers.Dense(1)(hidden_layer)  # [B, L, 1]

# 应用mask并进行加权求和(注意：不使用softmax归一化)
attention_weights = scores * mask  # [B, L, 1]
user_interest = tf.reduce_sum(keys * attention_weights, axis=1)  # [B, H]

DIEN:兴趣的演化建模

DIN 虽然成功捕捉了用户兴趣的多样性和局部激活特性，但它将用户历史行为视为无序集合，忽略了行为之间的时序依赖。而在真实场景中，用户兴趣不仅是多样的，更是在不断演化的

深度兴趣演化网络(Deep Interest Evolution Network, DIEN)(Zhou et al., 2019)被提出

DIEN 的核心观点是：不应只建模“行为”，而应建模行为背后随时间演化的“潜在兴趣状态”

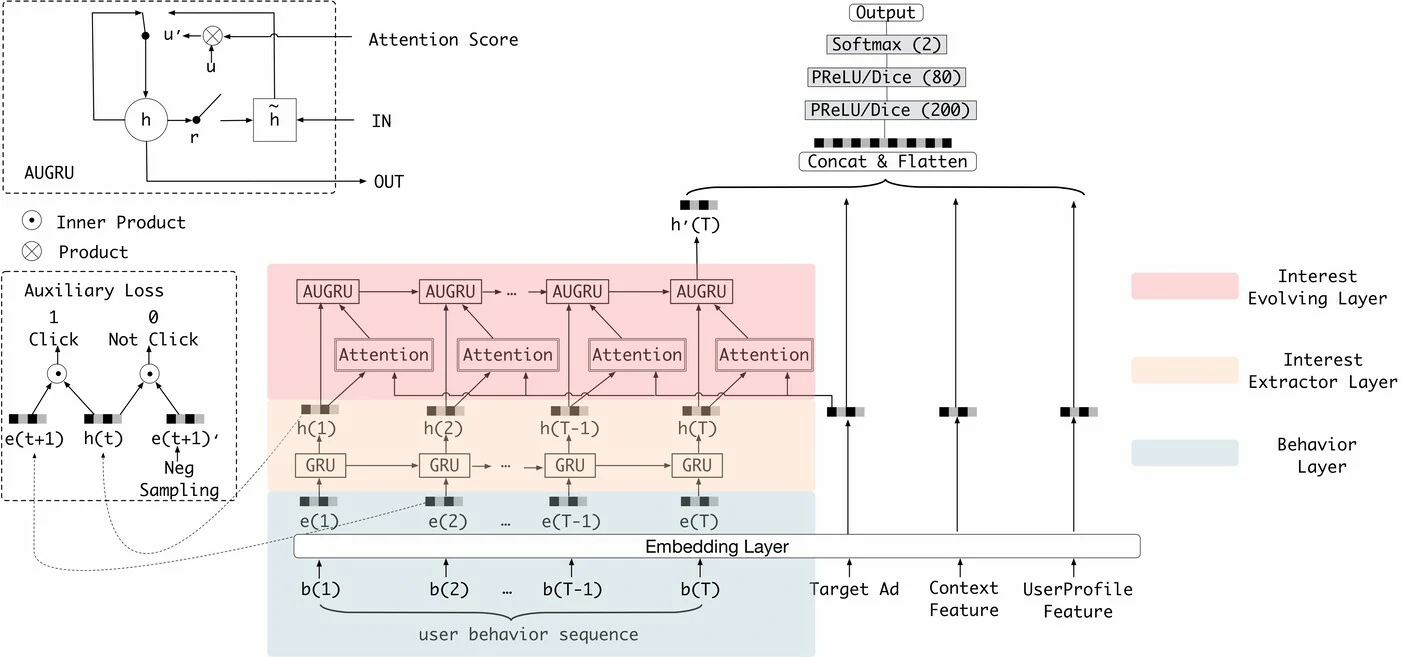
基于这一思想，DIEN 采用了一个两阶段结构

第一阶段：兴趣提取层 (Interest Extractor Layer)

该阶段的目标是：从原始行为序列中抽取更能表示潜在兴趣的兴趣状态序列

DIEN 使用 GRU 按时间顺序对用户行为 Embedding 序列${\boldsymbol e_1, \boldsymbol e_2, \dots, \boldsymbol e_T}$进行建模，得到隐状态$\boldsymbol h_t$，但仅依靠 GRU 的隐状态不足以精确刻画“兴趣”

DIEN 引入了关键创新：辅助损失(Auxiliary Loss)，其假设是：用户在时刻$t$的兴趣状态，直接决定了其在$t+1$时刻的行为

用$t$时刻的兴趣状态$\boldsymbol h_t$去预测用户在$t+1$时刻的真实行为$\boldsymbol e_{t+1}$，并通过负采样构造二分类损失：
$$
L_{aux}=-\frac{1}{N}\left(\sum_{i=1}^{N}\sum_{t=1}^{T}\log\sigma(\boldsymbol h^i_t,\boldsymbol e^i_{b[t+1]})+\log(1-\sigma(\boldsymbol h^i_t,\boldsymbol{\hat e^i_{b[t+1]}}))\right)
$$
该辅助损失与主任务 CTR 损失共同优化：
$$
L = L_{target} + \alpha L_{aux}
$$
这一额外监督信号在每个时间步约束 GRU，使其隐状态更贴近真实的潜在兴趣表示，而不仅仅是行为序列的编码

# 兴趣提取层的辅助损失计算
# interest_states: [batch_size, seq_len, hidden_units]
# pos_behaviors: [batch_size, seq_len, embedding_dim] 正样本行为
# neg_behaviors: [batch_size, seq_len, embedding_dim] 负样本行为

# 用t时刻的兴趣预测t+1时刻的行为
current_interests = interest_states[:, :-1, :]      # [B, T-1, H]
next_pos_behaviors = pos_behaviors[:, 1:, :]        # [B, T-1, D]
next_neg_behaviors = neg_behaviors[:, 1:, :]        # [B, T-1, D]

# 拼接兴趣和行为，送入MLP预测
pos_input = tf.concat([current_interests, next_pos_behaviors], axis=-1)
neg_input = tf.concat([current_interests, next_neg_behaviors], axis=-1)

# 预测正负样本的概率
pos_probs = auxiliary_mlp(pos_input)  # [B, T-1, 1]
neg_probs = auxiliary_mlp(neg_input)  # [B, T-1, 1]

# 二元交叉熵损失
aux_loss = -tf.reduce_mean(
    tf.math.log(pos_probs + 1e-8) + tf.math.log(1 - neg_probs + 1e-8)
)

第二阶段：兴趣演化层 (Interest Evolving Layer)

经过第一阶段，模型获得了兴趣状态序列$\boldsymbol h_1, \boldsymbol h_2, \dots, \boldsymbol h_T$

第二阶段的目标，就是对这个兴趣序列的演化过程进行建模

现实中，用户兴趣常伴随兴趣漂移，即在不同兴趣点之间切换

如果直接用标准 GRU 建模，历史中不相关的兴趣可能会干扰当前兴趣的演化

DIEN 设计了带注意力更新门的AUGRU(Attention-based GRU)，将 DIN 的注意力思想引入 GRU 的更新过程

注意力得分$a_t$由$t$时刻的兴趣状态$\boldsymbol h_t$和候选广告$\boldsymbol e_a$共同决定
$$
a_t = \frac{\exp(\boldsymbol h_t W \boldsymbol e_a)}{\sum_{j=1}^T\exp(\boldsymbol h_j W \boldsymbol e_a)}
$$
该注意力分数用于缩放 GRU 的更新门 $\boldsymbol{\tilde u’_t} = a_t \cdot \boldsymbol u’_t$

并据此更新隐状态：
$$
\boldsymbol h_t’ = (1 - \boldsymbol{\tilde u_t’}) \circ \boldsymbol h_{t-1}’ + \boldsymbol{\tilde u_t’} \circ \boldsymbol{\tilde h_t’}
$$
通过这种方式，AUGRU 在兴趣演化的每一步都会参考当前候选广告

与广告相关的兴趣被强化并持续传递，不相关的历史兴趣则被抑制，从而有效缓解兴趣漂移问题，使模型聚焦于与当前推荐任务最相关的兴趣演化路径

# AUGRU的前向传播
# interest_states: [batch_size, seq_len, hidden_units]
# target_item_embedding: [batch_size, embedding_dim]

# 1. 计算双线性注意力分数
# h_t * W * e_a
h_W = tf.tensordot(interest_states, bilinear_weight, axes=[[2], [0]])
target_expanded = tf.expand_dims(target_item_embedding, axis=1)
attention_scores = tf.reduce_sum(h_W * target_expanded, axis=2)  # [B, T]
attention_scores = tf.nn.softmax(attention_scores, axis=1)  # [B, T]

# 2. 逐步处理序列
hidden_state = tf.zeros([batch_size, hidden_units])
for t in range(seq_len):
    current_input = interest_states[:, t, :]     # [B, H]
    current_attention = attention_scores[:, t]   # [B]

    # 标准GRU计算
    update_gate = tf.nn.sigmoid(
        dense_input_update(current_input) + dense_hidden_update(hidden_state)
    )  # [B, H]

    reset_gate = tf.nn.sigmoid(
        dense_input_reset(current_input) + dense_hidden_reset(hidden_state)
    )  # [B, H]

    candidate_state = tf.nn.tanh(
        dense_input_candidate(current_input) +
        dense_hidden_candidate(reset_gate * hidden_state)
    )  # [B, H]

    # 关键：用注意力分数缩放更新门
    attention_expanded = tf.expand_dims(current_attention, axis=1)
    attention_expanded = tf.tile(attention_expanded, [1, hidden_units])
    attention_update_gate = attention_expanded * update_gate  # [B, H]

    # 更新隐藏状态
    hidden_state = (1 - attention_update_gate) * hidden_state + \
                   attention_update_gate * candidate_state

DSIN:从行为序列到会话序列

从 DIN 到 DIEN，模型对用户兴趣的理解从“静态相关”发展到“动态演化”，但它们仍将用户行为视为一条连续序列，在真实场景中，这一假设并不总是成立

用户行为往往呈现明显的会话结构：

在一个会话(Session)内，用户通常围绕单一意图进行集中操作；而在不同会话之间，兴趣点可能发生显著变化，呈现出会话内同质、会话间异质的特点。若直接用 RNN 建模这种带有明显“断层”的长序列，模型需要额外学习兴趣突变，建模效率和效果都会受限

深度会话兴趣网络(Deep Session Interest Network, DSIN)(Feng et al., 2019) 将“会话”作为分析用户行为的基本单元，并采用一种分层的思想来建模

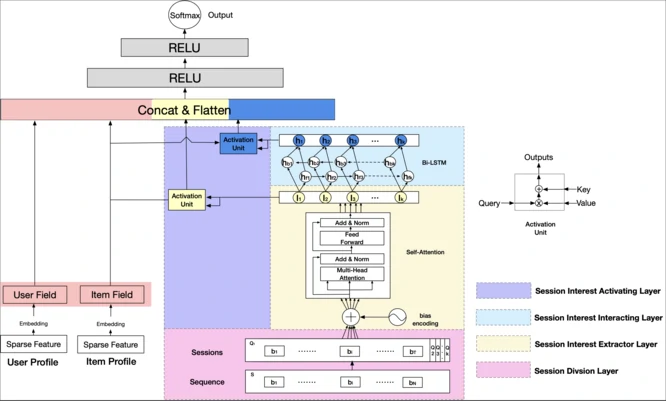
DSIN的技术实现：分层建模

DSIN 的整体结构可以分为四个层次

1. 会话划分层(Session Division Layer)

   这是模型的第一步，也是DSIN的基础。根据行为发生的时间间隔(如超过 30 分钟)，将原始用户行为长序列 $\mathbf S$ 切分为多个独立的会话短序列
   $$
   \mathbf Q = [\mathbf Q_1, \mathbf Q_2, …, \mathbf Q_K]
   $$
   这一层显式引入会话边界，使后续建模不再被长序列中的兴趣突变干扰

2. 会话兴趣提取层 (Session Interest Extractor Layer)

   该层的目标是：为每个会话提取一个核心兴趣表示

   然会话内意图相对集中，但不同历史行为的重要性仍不相同，DSIN 采用 自注意力机制(Self-Attention) 对会话内行为进行建模，捕捉行为之间的关联关系，并聚合关键信息，为每个会话 $\mathbf Q_k$ 生成一个兴趣向量 $\mathbf I_k$

3. 会话兴趣交互层 (Session Interest Interacting Layer)

   在上一层的基础上，模型得到的是一个更高层次的序列——会话兴趣序列：
   $$
   \mathbf I_1, \mathbf I_2, …, \mathbf I_K
   $$
   该序列反映了用户兴趣在更长时间尺度上的变化

   DSIN 使用 双向 LSTM(Bi-LSTM)对该序列建模，捕捉不同会话之间的演进关系，输出带上下文信息的会话兴趣表示
   $$
   [\mathbf H_1, \mathbf H_2, …, \mathbf H_K]
   $$

4. 会话兴趣激活层 (Session Interest Activating Layer)

   最后，DSIN 延续 DIN 的“局部激活”思想，引入候选广告$\mathbf X_I$,对会话兴趣进行注意力加权

   DSIN分别对会话兴趣提取层和交互层的输出都进行了激活
   $$
   \mathbf U^{I} = \sum_{k=1}^{K} a_{k}^{I} \mathbf I_{k} \qquad \mathbf U^{H} = \sum_{k=1}^{K} a_{k}^{H} \mathbf H_{k}
   $$
   最终，将这两个激活后的向量拼接，得到用户的最终兴趣表示

DSIN 通过引入会话这一中间层次，将原本复杂的长序列建模问题分解为两个更清晰的子问题：

• 会话内信息聚合(Self-Attention)
• 会话间信息传递(Bi-LSTM)

# 1. 会话兴趣提取：使用多头自注意力聚合会话内信息
# session_embeddings: [batch_size, sess_max_count, sess_max_len, embedding_dim]

session_interests = []
for sess_idx in range(sess_max_count):
    # 获取单个会话的embedding
    session_emb = session_embeddings[:, sess_idx, :, :]  # [B, L, D]

    # 多头自注意力捕获会话内物品之间的关系
    attention_output = tf.keras.layers.MultiHeadAttention(
        num_heads=att_head_num,
        key_dim=att_embedding_size,
        dropout=dropout_rate
    )(session_emb, session_emb)  # [B, L, d_model]

    # 平均池化得到会话级表示
    session_interest = tf.reduce_mean(attention_output, axis=1)  # [B, d_model]
    session_interests.append(session_interest)

# 构建会话兴趣向量的序列
session_interests = tf.stack(session_interests, axis=1)  # [B, K, d_model]

# 2. 会话兴趣交互：使用双向LSTM建模会话间的时序关系
# 构建上下文信息的会话兴趣序列
session_interactions = tf.keras.layers.Bidirectional(
    tf.keras.layers.LSTM(
        d_model // 2,
        return_sequences=True,
        dropout=dropout_rate
    ) # [B, K, d_model//2]
)(session_interests) # [B, K, d_model]

# 3. 会话兴趣激活：基于目标物品激活相关会话
# 扩展目标物品embedding以匹配会话维度
target_expanded = tf.expand_dims(target_item_embedding, axis=1)  # [B, 1, D]
target_repeated = tf.tile(target_expanded, [1, sess_max_count, 1])  # [B, K, D]

# 拼接会话特征 H_k 和目标物品
combined_H = tf.concat(
    [session_interactions, target_repeated], axis=-1
)  # [B, K, d_model + D]

# 计算注意力权重
attention_scores_H = tf.keras.layers.Dense(
    1, activation='tanh'
)(combined_H)
attention_weights_H = tf.nn.softmax(attention_scores_H, axis=1)  # [B, K, 1]

# 加权聚合会话特征
U_H = tf.reduce_sum(
    session_interactions * attention_weights_H, axis=1
)  # [B, d_model]

上面只体现了会话间交互后的兴趣的激活

还有浓缩的兴趣向量的激活

# 拼接会话兴趣 I_k 和目标物品
combined_I = tf.concat(
    [session_interests, target_repeated], axis=-1
)  # [B, K, d_model + D]

# 计算注意力权重
attention_scores_I = tf.keras.layers.Dense(
    1, activation='tanh'
)(combined_I)
attention_weights_I = tf.nn.softmax(attention_scores_I, axis=1) # [B, K, 1]

# 加权聚合会话兴趣
U_I = tf.reduce_sum(
    session_interests * attention_weights_I, axis=1
) # [B, d_model]

最后双路拼接

user_interest = tf.concat([U_I, U_H], axis=-1)  # [B, 2 * d_model]

总结

维度	DIN	DIEN	DSIN
主要动机	不同历史行为对不同目标贡献不同	用户兴趣随时间变化	用户行为具有会话结构
是否考虑时序	否	是	是(会话级)
序列建模方式	无	GRU / AUGRU	Bi-LSTM(会话序列)
注意力使用位置	行为 → 目标	兴趣 → 目标	会话 → 目标(双路)
关键创新点	局部激活单元	辅助损失 + AUGRU	分层建模 + 双路激活
应对兴趣漂移	×	部分缓解	更自然缓解
表达能力	中	高	更高
模型复杂度	低	中	中–偏高
适用场景	精排基础模型	长行为序列	行为断层明显
工程实现难度	低	中	较高

多目标建模

多目标建模（Multi-Task Learning, MTL）通过联合优化多个相关任务，实现推荐系统中用户体验与商业目标的协同提升。相较于独立建模，MTL 能够共享表示、减少参数规模，并通过知识迁移缓解数据稀疏问题。

在实际应用中，电商场景常联合优化 CTR、CVR 与 GMV，以避免单一指标带来的低质推荐

视频平台则同时建模播放完成率、评分预测与用户留存，以提升长期用户价值

然而，多目标建模也面临任务冲突、跷跷板效应及负迁移等挑战

CTR（Click-Through Rate，点击率） 点击次数/曝光次数

CVR（Conversion Rate，转化率） 转化次数/点击次数

GMV（Gross Merchandise Volume，成交额） GMV = 曝光量 × CTR × CVR × 客单价

曝光
 ↓ (CTR)
点击
 ↓ (CVR)
下单
 ↓ (客单价)
GMV

基础结构演进

Shared-Bottom

Shared-Bottom (Caruana, 1997) 模型作为多目标建模的奠基性架构，采用“共享地基+独立塔楼”的设计范式

其核心结构包含两个关键组件：

• 共享底层（Shared Bottom）：所有任务共用同一组特征转换层，负责学习跨任务的通用特征表示；
• 任务特定塔（Task-Specific Towers）：每个任务拥有独立的顶层网络，基于共享表示学习任务特定决策边界

这种架构的数学表达可描述为：
$$
\hat y_t = f_t(W_t \cdot g(W_s \mathbf x))
$$
其中 $\mathbf W_s$ 为共享层参数，$g(\cdot)$ 为共享特征提取函数，$f_t(\cdot)$ 为任务 $t$ 的预测函数

该结构隐含的核心假设是任务同质性：不同任务在底层特征空间中具有较高的一致性，仅需在高层进行任务区分

这个模型很容易联想到BERT，理念相似、实现与目标不同

维度	Shared-Bottom	BERT
抽象层级	训练结构设计	表示学习范式 + 具体模型
是否限定模型	不限定	强限定（Transformer）
是否必须预训练	否	是核心
任务关系假设	任务同时存在，且强相关	下游任务可以完全无关
训练方式	联合训练，loss 是多任务加权	先预训练再fine-tune

得益于这一设计，Shared-Bottom 在效率与泛化能力之间取得了良好平衡，其核心优势主要体现在以下几点

1. 共享层承载了模型的大部分参数，使整体参数规模显著降低
2. 参数共享本身具有正则化效应，可有效抑制单任务过拟合
3. 当任务之间存在相关性时，共享层能够实现知识迁移，从而提升样本稀缺任务的泛化性能

然而，Shared-Bottom 的硬共享机制也带来了明显局限，即负迁移问题

当不同任务的优化目标存在冲突时，共享层参数需同时响应多个方向不一致的梯度信号，导致优化过程出现内在矛盾

数学上，若任务$i$与任务$j$的损失梯度满足
$$
\nabla L_i \cdot \nabla L_j<0
$$
则共享参数的更新方向发生冲突，模型难以同时兼顾多个目标

内容平台中内容消费深度与广告曝光之间的权衡，深度阅读行为往往与广告点击行为呈负相关

这种“提升一项指标往往以牺牲另一项为代价”的现象，通常被称为跷跷板效应，也是 Shared-Bottom 架构进一步演进的重要动机

shared-bottom模型构建代码如下，先组装输入到shared-bottom网络中的特征dnn_inputs, 经过一个shared-bottom DNN网络，遍历创建各个任务独立的DNN塔，最后输出多个塔的预估值用于计算Loss

def build_shared_bottom_model(
        feature_columns,
        task_name_list,
        share_dnn_units=[128, 64],
        task_tower_dnn_units=[128, 64],
        ):
    # 输入层：将原始特征映射为 Keras 输入
    input_layer_dict = build_input_layer(feature_columns)

    # 嵌入层：为各特征组创建嵌入表，得到组内嵌入向量
    embedding_table_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding_"
    )

    # 合并嵌入：将多组嵌入拼接为共享 DNN 的输入
    dnn_inputs = concat_group_embedding(embedding_table_dict, 'dnn')

    # 共享底座：所有任务共享的特征抽取网络（Shared Bottom）
    shared_feature = DNNs(share_dnn_units)(dnn_inputs)

    # 任务塔：在共享特征上为每个任务构建独立塔并输出概率
    task_outputs = []
    for task_name in task_name_list:
        task_logit = DNNs(task_tower_dnn_units + [1])(shared_feature)
        task_prob = PredictLayer(name=f"task_{task_name}")(task_logit)
        task_outputs.append(task_prob)

    # 构建多任务模型：共享底座 + 多任务塔输出
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=task_outputs)
    return model

MMoE

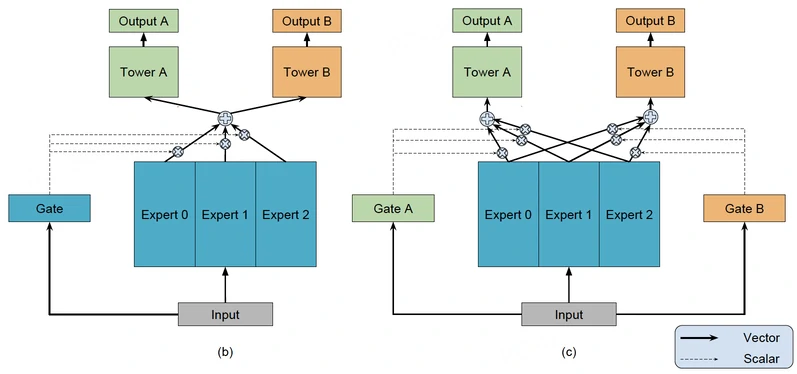
Shared-Bottom 在任务相关性较低时容易产生负迁移

OMoE（One-gate Mixture-of-Experts）将单一共享底层拆分为多个 Expert，并通过一个全局共享的门控网络对专家输出进行加权融合，其本质是“专家网络 + 全局门控”的两层结构

该设计通过提升底层特征表示的多样性，在一定程度上缓解了任务相关性较低时的负迁移问题

然而，由于 OMoE 的门控机制对所有任务共享，不同任务的梯度仍会同时作用于同一组专家

当任务目标存在冲突时，专家参数依然受到多任务梯度的直接干扰，因此并未从根本上解决多任务冲突问题

为进一步缓解这一问题，MMoE（Multi-gate Mixture-of-Experts）为每个任务引入独立的门控网络，将门控机制从“全局共享”升级为“任务自适应”，数学表达式可以表示为：
$$
\begin{aligned}
\mathbf e_k &= f_k(\mathbf x) \\
g_t(\mathbf x) &= \text{softmax}(\mathbf W_t \mathbf x) \\
\mathbf h_t &= \sum_{k=1}^K g_{t,k} \cdot \mathbf e_k \\
\hat y_t &= f_t(\mathbf h_t)
\end{aligned}
$$
其中

• $\mathbf x $表示底层的特征输入

• $\mathbf e_k$表示第$k$个专家网络的输出

• $g_t(\mathbf x)$表示第$t$个任务融合专家网络的门控向量

• $\mathbf h_t$表示第$t$个任务融合专家网络的输出

• $\hat y_t$表示第$t$个任务的预测结果

通过任务自适应门控，不同任务可以根据自身特性选择不同的专家组合

例如，在电商场景中，CTR 任务更侧重“即时兴趣”“价格敏感”等专家，而 CVR 任务则更关注“消费能力”“品牌忠诚”等长期特征

当任务$i$与$j$冲突时，MMoE的门控机制会让两个任务学习到不同专家的权重分布，例如某个专家$e_m$可能在任务$i$的门控网络中获得很高的权重$g_{i,m}$，而在任务$j$的门控网络中获得很低的权重$g_{j,m}$，从而有效减少梯度干扰

相比 OMoE，MMoE 在缓解任务冲突和负迁移方面更为有效，也成为多专家多任务建模的重要基础结构

核心代码

先组装输入到MoE网络中的特征dnn_inputs, 然后为每个任务创建一个门控网络输出最终融合专家网络的门控向量

最后为每个任务都创建一个任务塔，并且不同任务塔的输入都是对应任务的门控向量和多个专家网络融合后的向量

def build_mmoe_model(
        feature_columns,
        task_name_list,
        expert_nums=4,
        expert_dnn_units=[128, 64],
        gate_dnn_units=[128, 64],
        task_tower_dnn_units=[128, 64],
        ):
    # 输入层：原始特征 → Keras 输入
    input_layer_dict = build_input_layer(feature_columns)

    # 嵌入层：为各特征组创建嵌入表，得到组内嵌入向量
    embedding_table_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding_"
    )

    # 合并嵌入：拼接为专家与门控的共同输入
    dnn_inputs = concat_group_embedding(embedding_table_dict, 'dnn') # 对应x

    # 共享专家：多个并行 DNN（专家）供所有任务共享
    expert_outputs = [DNNs(expert_dnn_units, name=f"expert_{i}")(dnn_inputs)
                      for i in range(expert_nums)] # 对应e_k
    # 按专家维度堆叠，便于后续加权求和
    experts = tf.keras.layers.Lambda(lambda xs: tf.stack(xs, axis=1))(expert_outputs) # [B, E, D]

    # 任务门控：每个任务产生 softmax 权重，对专家加权融合
    task_features = []
    for idx, task_name in enumerate(task_name_list):
        gate_hidden = DNNs(gate_dnn_units, name=f"task_{idx}_gate_mlp")(dnn_inputs)
        gate_weights = tf.keras.layers.Dense(expert_nums, use_bias=False,
                                             activation='softmax',
                                             name=f"task_{idx}_gate_softmax")(gate_hidden)  # [B, E]
        # 加权融合：einsum('be,bed->bd') == sum_e w_e * expert_e
        task_mix = tf.keras.layers.Lambda(
            lambda x: tf.einsum('be,bed->bd', x[0], x[1])
        )([gate_weights, experts]) # [B, D]
        # einsum: 在左边出现、但在右边没出现的维度，会被“乘完再求和”
        task_features.append(task_mix) 

    # 任务塔：基于融合特征为每个任务建塔并输出概率
    task_outputs = []
    for task_name, task_feat in zip(task_name_list, task_features):
        task_logit = DNNs(task_tower_dnn_units + [1])(task_feat) # 最后输出一个值
        task_prob = PredictLayer(name=f"task_{task_name}")(task_logit)
        task_outputs.append(task_prob)

    # 构建模型：共享专家 + 任务门控 + 任务塔
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=task_outputs)
    return model

CGC

MMoE 通过为每个任务引入专属门控网络，使不同任务能够根据自身需求选择不同的专家组合，从而在一定程度上缓解多任务学习中的冲突问题

其结构仍存在一个根本性局限：所有专家对所有任务的门控均可见，这种“软隔离”的共享机制在实践中仍面临以下挑战

1. 负迁移未根除：
   • 干扰路径未切断：在 MMoE 中，即使某个专家 $e_m$ 在前向传播中几乎不被任务 $j$ 的门控选中，该专家仍属于任务 $j$ 的可选专家集合。因此，在反向传播阶段，任务 $j$ 的梯度仍可能更新 $e_m$ 的参数。当任务间冲突较强时，这种“潜在梯度通路”会导致共享表征被污染
   • 专家角色模糊：MMoE 未对专家的功能进行显式分工，一个专家可能同时承担共享知识与多个任务的特定信息，容易成为冲突的集中点。尤其在任务相关性较低的场景下，这种耦合会显著加剧负迁移。
2. 门控决策负担重：
   • 每个任务的门控需要在全部 $K$ 个专家上进行权重分配。随着专家数量增加（通常需要增大 $K$ 以提升模型容量），门控网络面临高维决策问题，训练稳定性下降，且更容易陷入次优解
   • 门控需要从包含多任务混杂信息的专家池中筛选有效表示，进一步增加了学习难度

为解决上述问题，CGC（Customized Gate Control） 通过硬性结构约束显式分离共享知识与任务特定知识，从而降低负迁移风险

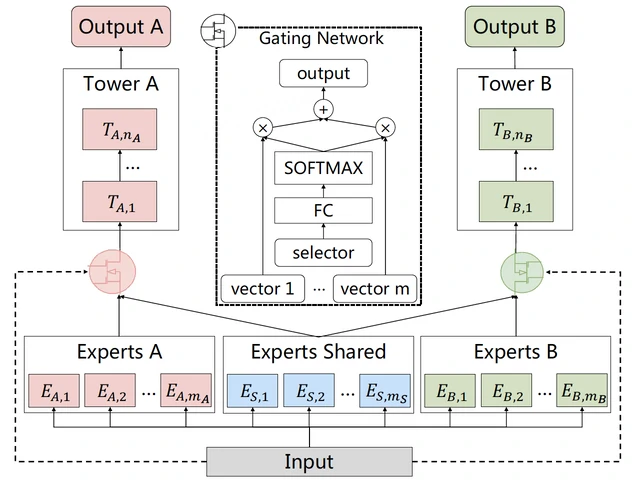
专家职责强制分离：

• 共享专家（C-Experts）：一组仅用于学习所有任务共性知识的专家，数量为 $M$，其输出为
  $$
  {\mathbf c_1, \mathbf c_2, …, \mathbf c_M}
  $$

• 任务专家 (T-Experts)：每个任务 $t$ 拥有独立的专家组，仅用于建模该任务的特有模式，数量为 $N_t$，其输出为
  $$
  {\mathbf t_t^1, \mathbf t_t^2, …, \mathbf t_t^{N_t}}
  $$

任务专属门控的输入限制：

• 任务 $t$ 的门控 $g_t$ 输入被严格限制为：共享专家输出 + 本任务专属专家输出
• 物理切断干扰路径：任务$t$的门控完全无法访问其他任务的专属专家，同样其他任务的梯度不会更新任务$t$的专属专家参数

CGC门控的计算如下：
$$
g_t(\mathbf x) = \text{softmax}\Big(\mathbf W_t \cdot \mathbf x + \mathbf b_t\Big) \\
\mathbf h_t = \sum_{k=1}^{M} g_{t,k} \cdot \mathbf c_k + \sum_{j=1}^{N_t} g_{t, M+j} \cdot \mathbf t_t^j\\
\hat y_t = f_t(\mathbf h_t)
$$
其中：

• $\mathbf W_t, \mathbf b_t$ 为任务 $t$ 门控的参数
• $g_{t,k}$ 表示第 $k$ 个共享专家的权重
• $g_{t,M+j}$ 表示任务 $t$ 的第 $j$ 个专属专家的权重

MMoE 通过门控“弱选择”专家，而 CGC 通过结构“硬隔离”专家

def cgc_net(
        input_list,
        task_num,
        task_expert_num,
        shared_expert_num,
        task_expert_dnn_units,
        shared_expert_dnn_units,
        task_gate_dnn_units,
        shared_gate_dnn_units,
        leval_name=None,
        is_last=False):
    """CGC（共享专家 + 任务门控）核心结构（简化版）
    - 每个任务：拥有若干 Task-Experts；
    - 全局：拥有若干 Shared-Experts；
    - 每个任务 Gate 产生 softmax 权重，对其 Task-Experts 与 Shared-Experts 加权融合；
    - 若非最后一层：再用 Shared-Gate 融合所有任务的 Task-Experts 与 Shared-Experts，供下一层共享使用。
    input_list：为方便处理，给每个任务复制一份相同输入，最后一个为共享输入，长度 = task_num + 1
    """

    # 任务专家：每个任务创建 task_expert_num 个专家
    task_expert_list = []
    for i in range(task_num):
        task_expert_list.append([
            DNNs(task_expert_dnn_units, name=f"{leval_name}_task_{i}_expert_{j}")(input_list[i])
            for j in range(task_expert_num)
        ])

    # 共享专家：创建 shared_expert_num 个专家（共享输入使用 input_list[-1]）
    shared_expert_list = [
        DNNs(shared_expert_dnn_units, name=f"{leval_name}_shared_expert_{i}")(input_list[-1])
        for i in range(shared_expert_num)
    ]

    # 任务门控与融合：对当前任务的（Task + Shared）专家集合进行 softmax 加权求和
    cgc_outputs = []
    fusion_expert_num = task_expert_num + shared_expert_num
    for i in range(task_num):
        cur_experts = task_expert_list[i] + shared_expert_list
        experts = tf.keras.layers.Lambda(lambda xs: tf.stack(xs, axis=1))(cur_experts)  # [B, E, D]

        gate_hidden = DNNs(task_gate_dnn_units, name=f"{leval_name}_task_{i}_gate")(input_list[i])
        gate_weights = tf.keras.layers.Dense(fusion_expert_num, use_bias=False, activation='softmax')(gate_hidden)  # [B, E]

        # 加权融合：einsum('be,bed->bd') == sum_e w_e * expert_e
        fused = tf.keras.layers.Lambda(lambda x: tf.einsum('be,bed->bd', x[0], x[1]))([gate_weights, experts])
        cgc_outputs.append(fused)

    # 若非最后一层：共享门控融合所有任务专家与共享专家，作为下一层共享输入
    # 这部分是PLE的
    if not is_last:
        # 展平所有任务的专家 + 共享专家
        all_task_experts = [e for task in task_expert_list for e in task]
        cur_experts = all_task_experts + shared_expert_list
        experts_all = tf.keras.layers.Lambda(lambda xs: tf.stack(xs, axis=1))(cur_experts)  # [B, E_all, D]
        cur_expert_num = len(cur_experts)

        shared_gate_hidden = DNNs(shared_gate_dnn_units, name=f"{leval_name}_shared_gate")(input_list[-1])
        shared_gate_weights = tf.keras.layers.Dense(cur_expert_num, use_bias=False, activation='softmax')(shared_gate_hidden)  # [B, E_all]
        shared_fused = tf.keras.layers.Lambda(lambda x: tf.einsum('be,bed->bd', x[0], x[1]))([shared_gate_weights, experts_all])
        cgc_outputs.append(shared_fused)

    return cgc_outputs

PLE

CGC 通过结构约束实现了共享知识与任务特定知识的显式分离，但其本质仍是单层专家融合结构，表征学习深度有限

受深度神经网络逐层抽象特征的启发，PLE (Progressive Layered Extraction) 通过纵向堆叠多个 CGC 单元，构建深层多任务架构，实现知识的渐进式提取与融合

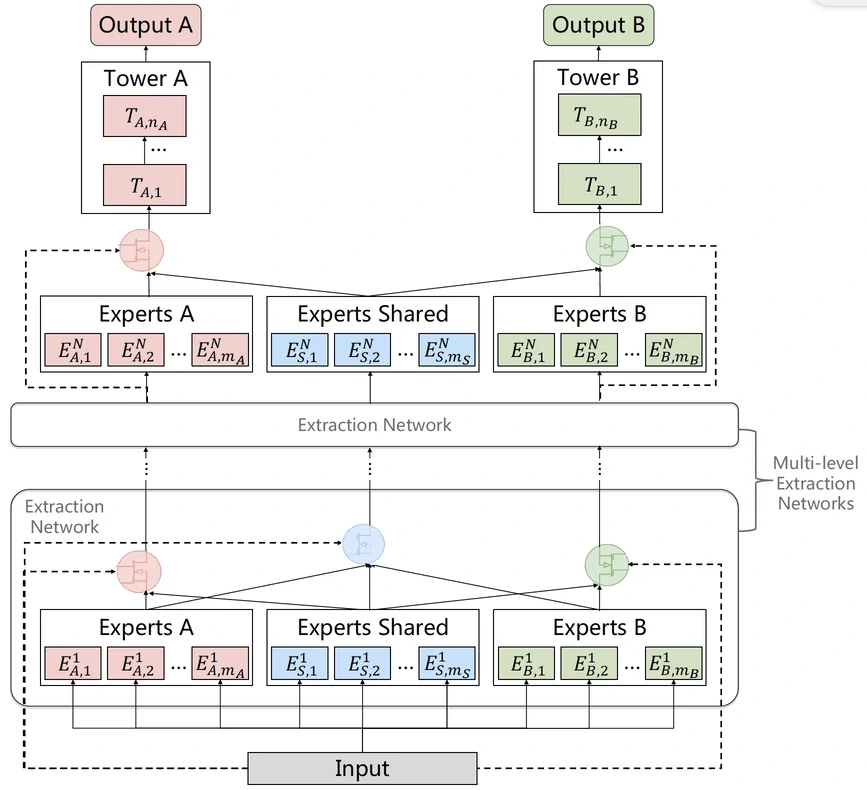
PLE 由 $L$ 个 CGC 层级组成

第1层 (输入层) CGC：

• 输入：原始特征 $\mathbf x$

• 结构：一个标准 CGC 模块

  $M^{(1)}$ 个共享专家（C-Experts），每个任务 $t$ 有 $N_t^{(1)}$ 个任务专家（T-Experts），以及对应的任务门控 $g_t^{(1)}$

• 作用：在原始特征空间中进行初步的共享/任务特定知识分离

• 输出：每个任务的初步融合表示 $\mathbf h_t^{(1)}$，以及（更常见地）该层所有专家的输出集合，作为下一层的输入

第 $l$ 层（$l \ge 2$）CGC：

• 输入：第 $l-1$ 层所有专家（C + T）的输出，设其总数为 $E^{(l-1)}$

• 结构：一个新的 CGC 模块

  $M^{(l)}$ 个共享专家，每个任务 $t$ 的 $N_t^{(l)}$ 个任务专家，新的任务门控 $g_t^{(l)}$

• 处理：在更高层、更加丰富的特征空间中再次执行显式知识分离（新的共享 / 任务专家），并通过门控完成任务感知的融合

• 输出：当前层的任务表示 $\mathbf h_t^{(l)}$，或该层所有专家的输出集合

输出层（第 $L$ 层）：

• 最后一层 CGC 的任务输出 $\mathbf h_t^{(L)}$输入至各自的任务塔网络 $f_t$，得到最终预测：
  $$
  \hat y_t = f_t(\mathbf h_t^{(L)})
  $$

CNN	PLE
卷积核（Kernel）	专家（Expert）
通道（Channel）	专家维度
Feature Map	任务 / 共享表征
1×1 Conv	Gate（加权融合）
Conv Block	CGC Block

def build_ple_model(
        feature_columns,
        task_name_list,
        ple_level_nums=1,
        task_expert_num=4,
        shared_expert_num=2,
        task_expert_dnn_units=[128, 64],
        shared_expert_dnn_units=[128, 64],
        task_gate_dnn_units=[128, 64],
        shared_gate_dnn_units=[128, 64],
        task_tower_dnn_units=[128, 64],
        ):
    # 1) 输入与嵌入：构建输入层/分组嵌入，拼接为 PLE 的共享输入
    input_layer_dict = build_input_layer(feature_columns)
    group_embedding_feature_dict = build_group_feature_embedding_table_dict(
        feature_columns, input_layer_dict, prefix="embedding_"
    )
    dnn_inputs = concat_group_embedding(group_embedding_feature_dict, 'dnn')

    # 2) 级联 PLE（CGC）层：每层包含“任务专家 + 共享专家 + 门控”，最后一层仅输出任务特征
    task_num = len(task_name_list)
    ple_input_list = [dnn_inputs] * (task_num + 1)  # 前 task_num 为各任务输入，末尾为共享输入
    for i in range(ple_level_nums):
        is_last = (i == ple_level_nums - 1)
        ple_input_list = cgc_net(
            ple_input_list,
            task_num,
            task_expert_num,
            shared_expert_num,
            task_expert_dnn_units,
            shared_expert_dnn_units,
            task_gate_dnn_units,
            shared_gate_dnn_units,
            leval_name=f"cgc_level_{i}",
            is_last=is_last
        )

    # 3) 任务塔与输出：将各任务特征送入塔 DNN，得到每个任务的概率输出
    task_output_list = []
    for i in range(task_num):
        task_logit = DNNs(task_tower_dnn_units + [1])(ple_input_list[i])
        task_prob = PredictLayer(name="task_" + task_name_list[i])(task_logit)
        task_output_list.append(task_prob)

    # 4) 构建模型：输入为所有原始输入层，输出为各任务概率
    model = tf.keras.Model(inputs=list(input_layer_dict.values()), outputs=task_output_list)
    return model

多目标损失融合

在多目标学习中，多个任务通常对应多个损失函数，其联合优化策略在模型结构确定后，成为影响最终性能的关键因素。最简单的做法是对各任务损失进行加权求和：
$$
Loss_{total} = \sum_i w_i L_i
$$
其中，$L_i$ 表示第 $i$ 个任务的损失，$w_i$ 为对应权重

然而，手工加权方法存在三个根本性问题：

• 量级失衡：不同任务损失值尺度差异大（如CTR损失通常在0.1-0.5，CVR损失可达2.0+），导致大损失主导优化；
• 收敛异步：稀疏任务收敛慢，密集任务收敛快，造成过拟合与欠拟合并存
• 梯度冲突：任务梯度方向不一致甚至相反，造成更新相互抵消（如CTR与CTR任务梯度夹角>90°）

重点介绍三类代表性方案

Uncertainty Weight

基于不确定性加权损失（Uncertainty Weighted Loss, UWL）(Kendall et al., 2018)

UWL的核心思想是根据任务的不确定性动态调整权重，其基本思想是：不确定性越高的任务，对参数更新的影响应越小

损失函数形式为：
$$
Loss = \sum _i\frac{1}{2\sigma_i^2} \mathcal L_i(\mathbf W) + \log \sigma_i
$$
其中，$\sigma_i$ 为任务 $i$ 的不确定性参数，是可学习的

当任务损失较大或噪声较高时，$\sigma_i$ 增大，对应权重 $\frac{1}{\sigma_i^2}$ 减小，模型自动降低该任务对共享参数更新的影响

该方法无需人工设权，但假设损失服从特定概率分布，适用性依赖任务建模假设

GradNorm

GradNorm(Chen et al., 2018)直接从梯度层面解决多任务训练不平衡问题，同时考虑：

• 任务损失的梯度量级
• 不同任务的学习速度

梯度量级定义：
$$
G_W^{(i)}(t) = ||\nabla_W w_{i}(t) L_{i}(t)||_2
$$

$$
\overline G_W(t) = E_{task}[G_W^{(i)}(t)]
$$

其中 $W$ 是所有任务loss对多个任务最后一层共享参数

$G_{W}^{(i)}(t)$表示任务$i$加权后的Loss，对共享参数$W$的梯度；$\overline G_{W}(t)$表示所有任务对共享参数梯度的均值

学习速度定义：
$$
\begin{aligned}
\tilde L_i(\tilde t) = L_i(t) / L_i(0)\\
r_i(t) = \frac{\tilde L_i(t)}{E_{\text{task}}[\tilde L_i(t)]}
\end{aligned}
$$
$L_i(t)$表示的是训练的第$t$时刻，任务$i$的Loss值，所以$\tilde{L}_i(\tilde{t})$表示的是任务$i$在第$t$时刻的相对第0时刻的损失比率，该值如果越小的话则代表该任务loss收敛的比较快

$r_i(t)$则是在$L_i(t)$的基础上做了一次归一化，让所有任务之间的速率相对可以比较

最终的梯度损失函数定义为如下表达式：
$$
L_{\text{grad}} = \sum_i \left| G_W^{(i)}(t) - \overline G_W(t) \times [r_i(t)]^\alpha \right|_1
$$
GradNorm 通过最小化该梯度损失，动态调整各任务的损失权重，使：

• 梯度过大的任务被抑制
• 收敛过快的任务被减速
• 多任务训练保持同步

Pareto Optimization

当任务之间存在根本性梯度冲突时（优化一个任务必然损害另一个），加权求和方法不再适用，需要引入帕累托优化框架(Lin et al., 2019)

多目标优化问题定义为：
$$
\min_{\theta} \mathbf L(\theta) = \min_{\theta} (\mathcal L_1(\theta), \mathcal L_2(\theta), …, \mathcal L_T(\theta))
$$
帕累托最优解指：不存在另一解能在不恶化至少一个任务的情况下改进任一任务

核心思想

将多目标损失合并为加权和，并利用 KKT 条件动态调整权重，使优化方向指向帕累托前沿：
$$
\mathcal L(\theta) = \sum_{i=1}^{K} w_i \mathcal L_i (\theta)
$$
其中 $w_i$ 为可学习的权重，满足 $\sum w_i = 1$ 且 $w_i \geq c_i$（$c_i$ 为权重下限）

优化流程

1. 固定权重，更新模型参数 $\theta$：通过梯度下降最小化加权损失 $\mathcal{L}(\theta)$，即常规的模型训练步骤

2. 固定模型参数，优化权重 $w_i$
   $$
   \min_w\left|\sum_{i=1}^{K} w_{i} \nabla_\theta \mathcal L_{i}(\theta)\right|_2^2
   $$
   约束条件：$\sum w_i = 1$，$w_i \geq c_i$

   通过变量松弛与投影，将该问题转化为带约束的二次规划并高效求解

总结

维度	Uncertainty Weight (UWL)	GradNorm	Pareto Optimization
核心视角	概率建模	梯度平衡	多目标优化理论
解决的主要问题	Loss 量级失衡	梯度量级 + 收敛速度不一致	根本性梯度冲突
权重来源	任务不确定性 $\sigma_i$	梯度统计量	显式可学习权重 $w_i$
是否显式考虑梯度方向	❌	❌（仅量级）	✅
优化目标	加权 loss	梯度量级对齐	加权梯度范数最小
是否引入额外 loss	❌	✅（gradient loss）	❌
计算复杂度	低	中	高
实现复杂度	低	中	高
训练稳定性	高	中	中
工程可控性	低	中	高
适合任务关系	弱冲突 / 同质	中等冲突	强冲突 / 对立
常见应用	多回归 / 多分类	CTR + CVR	LTR / 强博弈任务

多场景建模

在现代大规模推荐系统中，用户的行为和兴趣往往呈现出高度的场景依赖性

这里的“场景”既可以是不同业务位置（如首页推荐、详情页推荐、购物车推荐），也可以是不同流量入口、用户状态、设备类型或时间上下文

试图用单一全局模型覆盖所有场景，通常会面临以下问题：

1. 场景特性被淹没：数据量大的主流场景主导训练过程，模型难以刻画小场景或特性鲜明场景的独有模式
2. 数据稀疏性突出：新场景、低流量场景或长尾用户缺乏足够样本，独立建模效果不稳定
3. 参数与维护成本高：为每个场景单独训练完整模型，参数冗余严重，且难以实现场景间的知识迁移

多场景建模（Multi-scenario / Multi-domain Modeling）其核心目标是：充分利用多个场景数据之间的潜在“共性”来提升模型的泛化能力和鲁棒性，同时精细地识别和建模不同场景的“特性”差异，以实现场景间的差异化精准推荐

多场景建模的目标是：既要“合”得好（共享有益知识），也要“分”得清（保留独有特性）

两大类主流且互补的范式

• 多塔结构建模范式：

  • 在模型结构层面进行显式划分，构建一个或多个共享塔（Shared Tower），学习跨场景的共性知识；
  • 为每个场景（或场景组）构建场景专属塔（Scenario-specific Tower），建模场景特有模式
  • 通过门控、路由等机制控制共享与专属信息的融合方式

  该范式强调结构上的“硬区分”，具有良好的可解释性与稳定性

• 动态权重建模范式：不显式划分模型结构，而是利用场景上下文信息（如场景 ID、场景属性、用户在该场景下的行为）

  • 动态调整特征表示、网络权重或损失权重
  • 在保持模型主体共享的同时，使模型行为随场景自适应变化

  该范式强调行为上的“软适配”，灵活性更强