RC文氏电桥分析

设计详细说明：

论文资料整理：

论文中传递函数的推导：
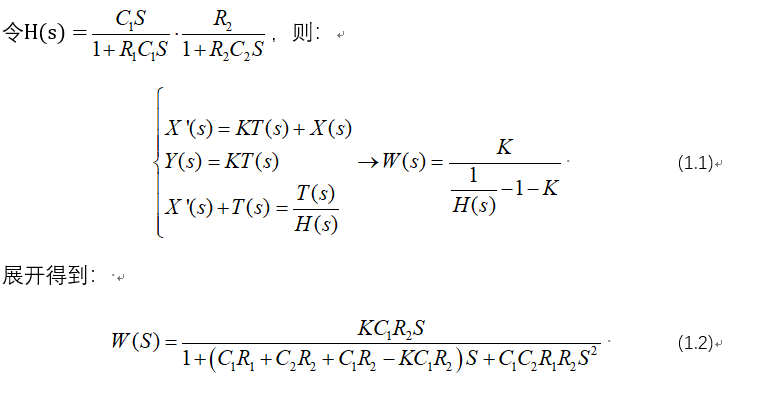
稳定性的简要判断：

劳斯判据：根都在复平面左半平面，系统稳定

K的7种取值下分析：

代码块：

绘制对应零极点图：（lingjidian.m文件）

clc%清空命令行

clear%从工作区中删除项目、释放系统内存

clf%清空当前图窗窗口

K=11;%可修改放大倍数

%可修改参数

R=1e4;

C=1e-8;

RC=R\*C;

fenzi=[K 0];

fenmu=[RC 3-K 1/RC];

sys=tf(fenzi,fenmu);%构成传递函数

poles=roots(fenmu);%求极点

pzmap(sys,'r');% 零极点分布图显示

绘制时域单位冲击响应函数：（chongjixiangyinghanshu.m文件）

clc%清空命令行

clear%从工作区中删除项目、释放系统内存

clf%清空当前图窗窗口

K=11;%可修改放大倍数

%可修改参数

R=1e4;

C=1e-8;

RC=R\*C;

fenzi=[K 0];

fenmu=[RC 3-K 1/RC];

sys=tf(fenzi,fenmu);%构成传递函数

t=0:6\*1e-6:1e-3; %控制绘图的时间区间

impulse(fenzi,fenmu,t) %绘图

title(['K=',num2str(K),'冲激响应函数'])

xlabel('时间t')

K>5(取K=11)

Matlab结果：

零极点图：

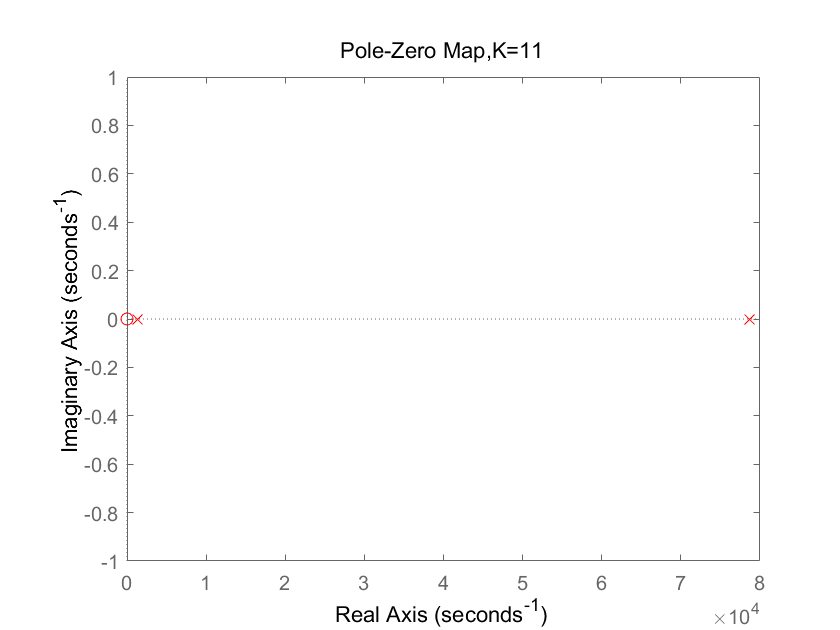
零极点为两个不同的正实数，收敛域不过jw轴，系统不稳定

冲激响应函数：

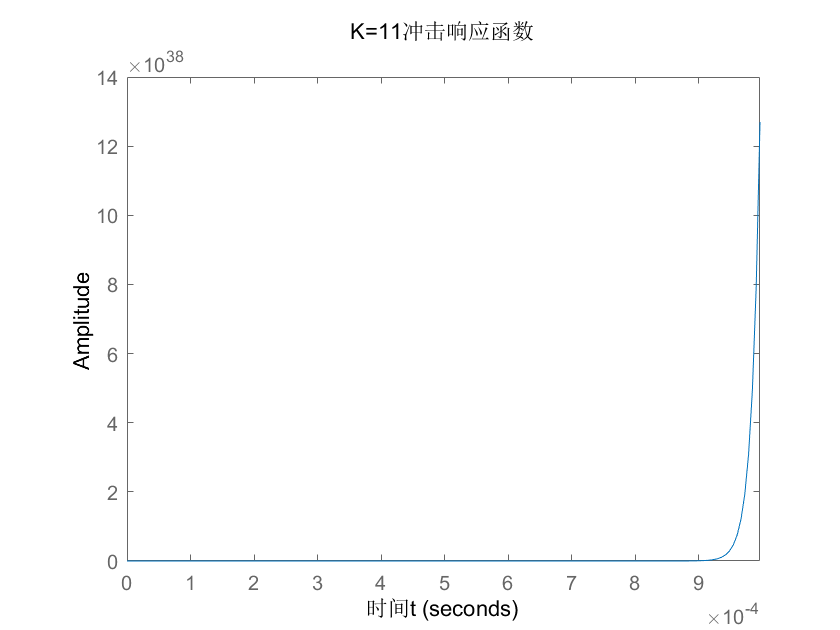
可知冲激响应函数单调上升，无界，系统不稳定

Multisim仿真：（之后不再给出电路图，仅改变大小来改变K）

输出端产生的信号近似等于方波信号：
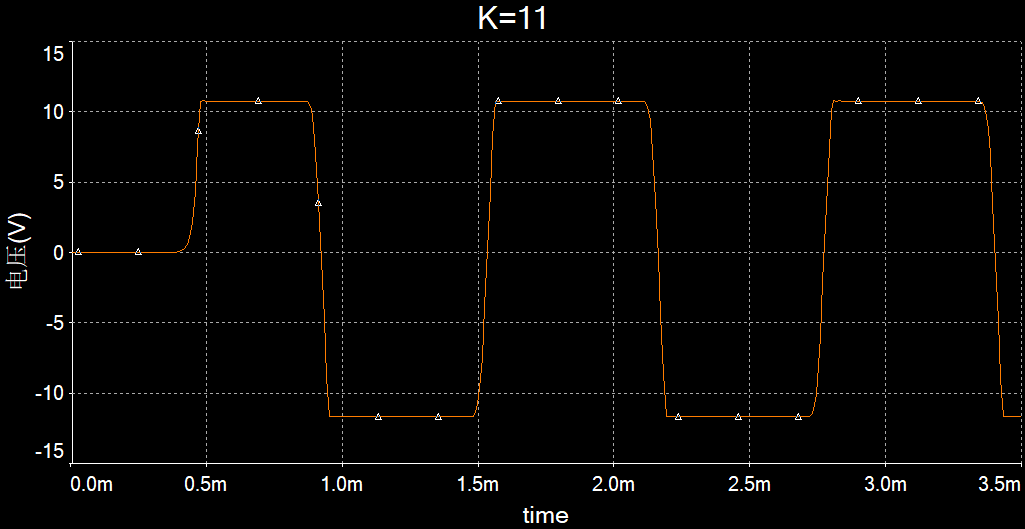
K=5

Matlab结果：

零极点图：

零极点为两个相等的正实数，收敛域不过jw轴，系统不稳定

冲激响应函数：

可知冲激响应函数单调上升，无界，系统不稳定

Multisim仿真：

输出端产生的信号失真不能实现稳定的单一频率的震荡，在 t=0
开始到第一次到达峰值可以看到一段电压呈指数形式增长的曲线。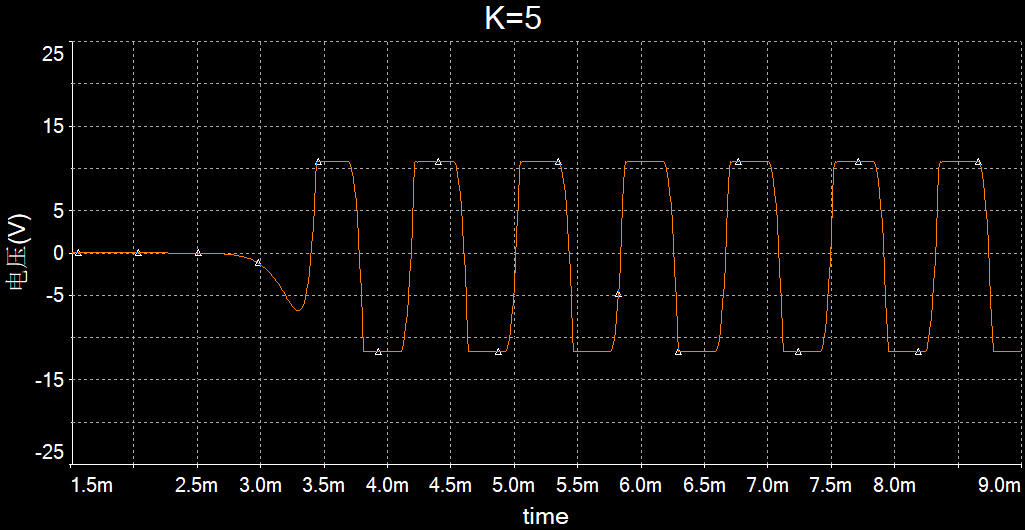
3<K<5（取K=3.5）

Matlab结果：

零极点图：

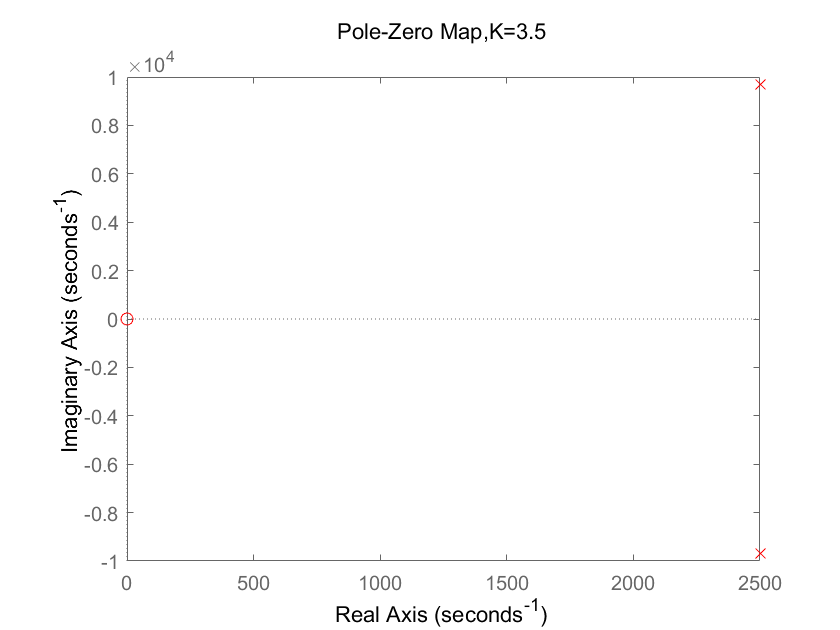
零极点为两个共轭且实部大于0的虚数，收敛域不过jw轴，系统不稳定

冲激响应函数：

可知冲激响应函数增幅振荡上升，无界，系统不稳定

Multisim仿真：

输出端产生的信号经过振荡后类似K=5的情况，振荡时间变长：
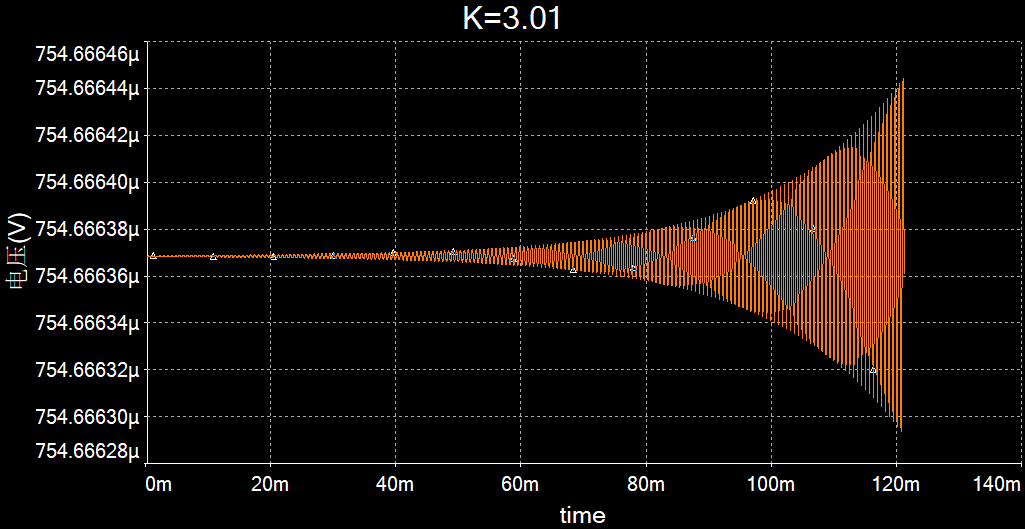
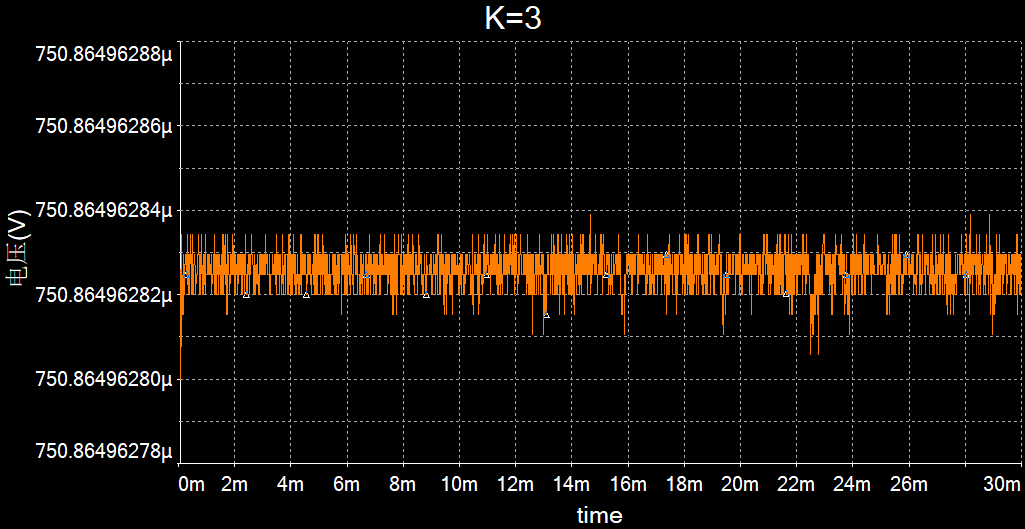
K=3

Matlab结果：

零极点图：

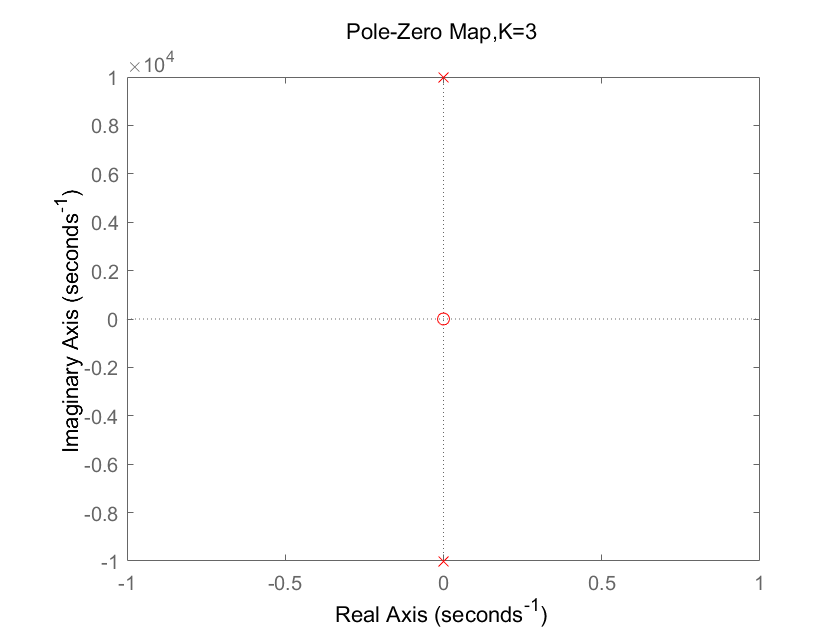
零极点为两个共轭的纯虚数，在jw轴上仅通过零极点不能判断系统是否稳定

冲激响应函数：

可知冲激响应函数等幅振荡，有界，系统稳定

Multisim仿真：

输出端的信号在一个范围内无规则振荡
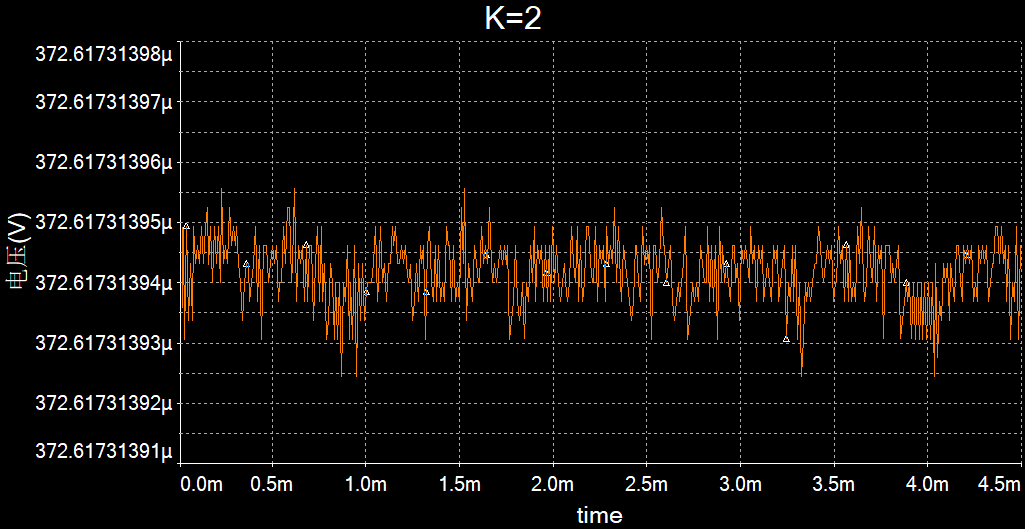
1<K<3(取K=2)

Matlab结果：

零极点图：

零极点为两个共轭且实部小于0的虚数，收敛域过jw轴，可判断收敛

可知冲激响应函数振荡衰减，有界，系统稳定，趋于0

Multisim仿真：

输出端的信号在一个范围内无规则振荡趋于0
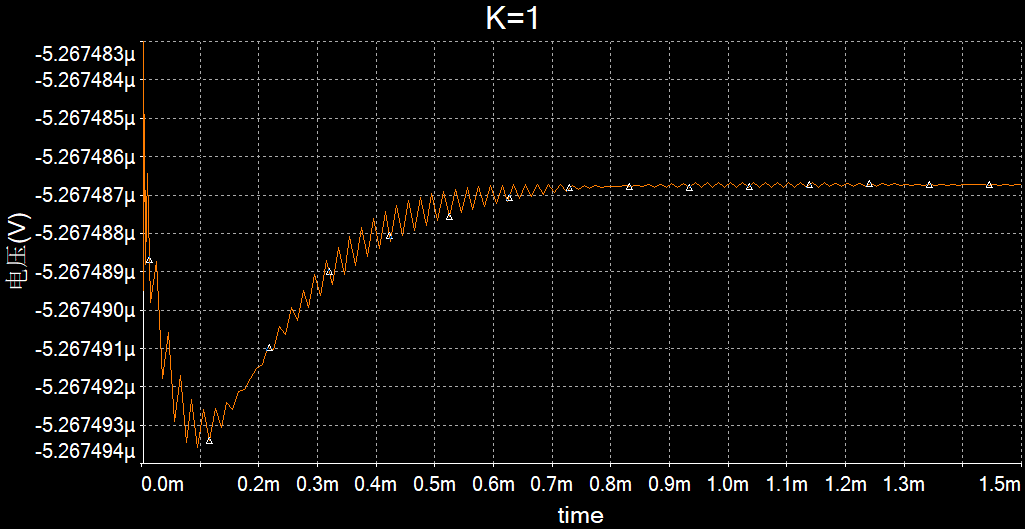
K=1

Matlab结果：

零极点图：

零极点为两个相等的负实数，收敛域过jw轴，可判断收敛

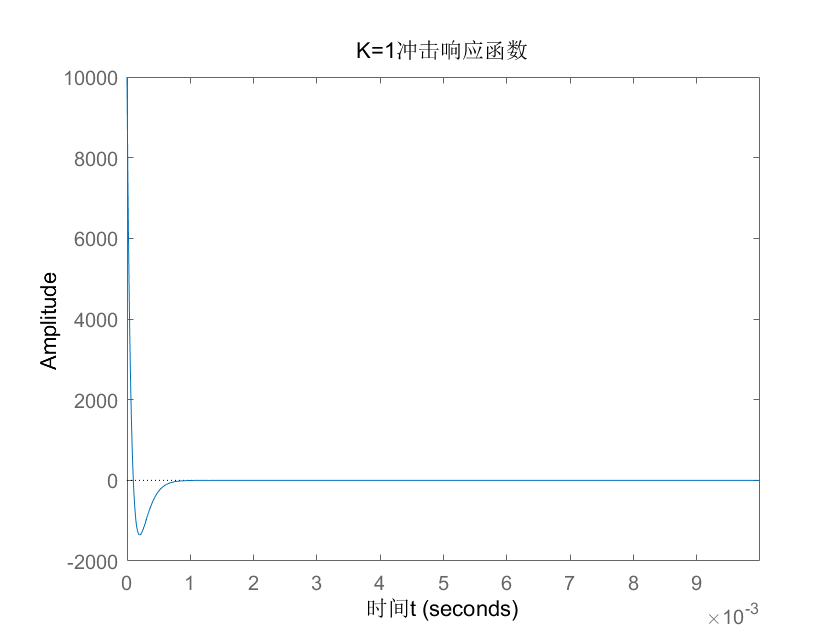
可知冲激响应函数非振荡衰减但也是衰减，有界，系统稳定，趋于0

Multisim仿真：

输出端的信号在一个振荡后趋于0
K<1

Matlab结果：

零极点图：

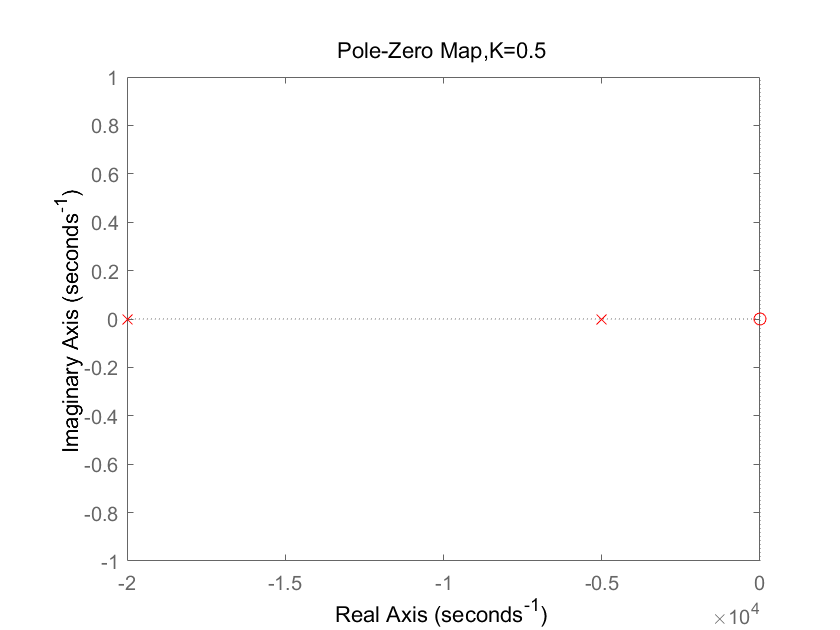
零极点为两个不相等的负实数，收敛域过jw轴，可判断收敛

可知冲激响应函数非振荡衰减但也是衰减，有界，系统稳定，趋于0

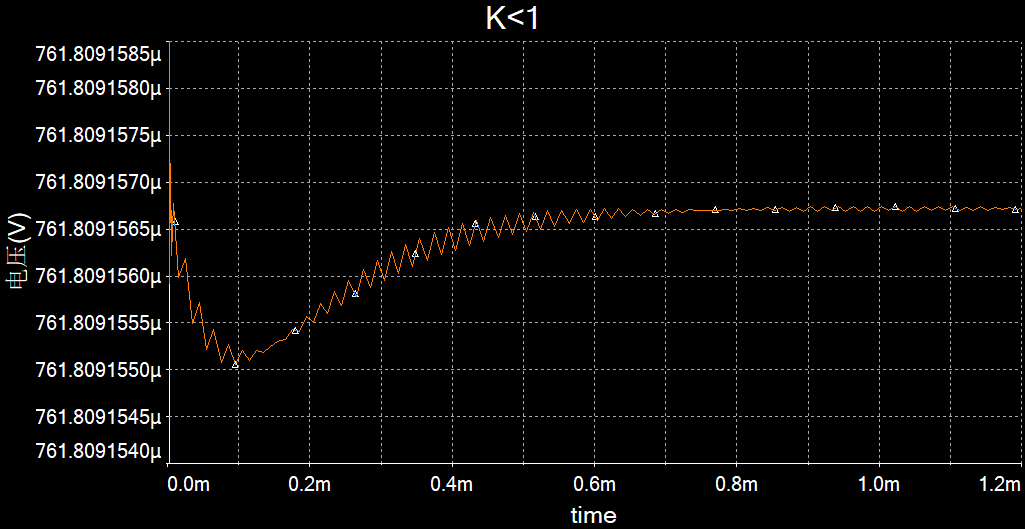
Multisim仿真：

输出端的信号在一个振荡后趋于0